机器学习（12）

聚类的核心思想和原理

人以类聚，物以群分

分类和聚类案例：

在水果分类问题中，我们事先已经定义好了水果类别 ，例如苹果、香蕉和橙子，并且拥有一批带有明确标签的训练数据。模型在训练阶段学习"特征与类别之间的对应关系"。当出现一个新的水果样本，模型会根据已经学到的规则，判断该水果最可能属于哪一个已知类别，比如判定为"苹果"。

分类的本质：在已知类别集合的前提下，对新样本进行归类，是一种有监督学习方法。

在水果聚类问题中，我们并不知道水果的具体类别，也没有任何标签信息，只有水果的特征数据，如颜色、形状、重量等。算法仅根据样本之间的相似性进行分析。通过计算特征上的相近程度，算法会自动将水果划分为若干组，例如将"圆形、重量相近的水果"分为一组，将"细长、较轻的水果"分为另一组。聚类完成后，再根据每一组水果的共同特征，对这些簇进行解释或命名（如某一簇可能对应苹果或橙子）。

聚类的本质：在类别未知的情况下，自动发现数据的内在结构，是一种无监督学习方法。

聚类(Clustering)特点：

同簇高相似度
不同簇高相异度
同类尽量相聚
不同类尽量分离

对比	分类	聚类
是否有标签	✅ 有	❌ 无
学习方式	监督学习，训练获得分类器	无监督学习，不关注类别标签
是否提前定义类别	是	否

主要聚类方法：

划分式聚类：k-means、k-means++、bi-kmeans
密度聚类：DBSCAN、OPTICS
层次化聚类：Agglomerative、Divisive
其他方法：量子聚类、核聚类、谱聚类

聚类步骤：

数据准备：标准化和降维
特征选择：最有效特征
特征提取：特征转换
聚类：基于距离做相似度度量，得到簇
结果评估：分析聚类结果

K-means和分层聚类

K-means

核心思想：

根据样本点与簇质心距离判定
以样本间距离衡量相似度

步骤：

选择k个初始质心
计算样本到各个质心的欧氏距离，归入最近的簇
计算新簇的质心

数据准备

python 复制代码

import os
os.environ["OMP_NUM_THREADS"] = "1"
os.environ["MKL_NUM_THREADS"] = "1"
os.environ["OPENBLAS_NUM_THREADS"] = "1"
os.environ["NUMEXPR_NUM_THREADS"] = "1"
import warnings
warnings.filterwarnings("ignore", message=".*KMeans is known to have a memory leak.*")

import numpy as np
import matplotlib.pyplot as plt

from sklearn.datasets import make_blobs
# centers=5 表示生成的数据围绕 5 个"中心点"，也就是生成 5 个簇（5 类）
X,y = make_blobs(n_samples=250,centers=5,n_features=2,random_state=0)

KMeans算法

python 复制代码

from threadpoolctl import threadpool_limits
from sklearn.cluster import KMeans
with threadpool_limits(limits=1):
    kmeans = KMeans(n_clusters=5, random_state=0).fit(X)

# 绘制聚类中心
center = kmeans.cluster_centers_

plt.scatter(X[:,0],X[:,1],c=kmeans.labels_)
plt.scatter(center[:,0],center[:,1],color='red',marker='x')
plt.show()

层次聚类

核心思想：

按照层次把数据划分到不同层的簇，形成树状结构
在树形结构上不同层次划分，可以得到不同粒度的聚类
过程分为自底向上的聚合聚类和自顶向下的分类聚类

|--------|------------------------|----------------------|
| 方法 | 自底向上 | 自顶向下 |
| 特点 | 每个样本看成一个簇簇间距离最小的相似簇合并 | 所有的样本看成一个簇逐渐分裂成更小的簇 |

簇间相似度度量

最大距离（Complete-link，最远邻）

两个簇中距离最远的两个样本决定簇间相似度。

最小距离（Single-link，最近邻)

两个簇中距离最近的两个样本决定簇间相似度

平均距离（Average-link，平均相似度）

计算两个簇中所有样本对距离的平均值

linkage方法	合并依据	簇形状	特点
ward	方差增量最小	紧凑、球形	默认首选
single	最近点	拉长	易链化
complete	最远点	紧凑	抗噪好
average	平均距离	中等	稳定折中

层次聚类

python 复制代码

from sklearn.cluster import AgglomerativeClustering
# 自底向上的聚类方法：ward方法合并后 簇内平方误差（方差）增加最小 的两个簇
# single：两个簇中 最近的两个样本 决定是否合并
# complete：两个簇中 最远的两个样本 决定是否合并
# average：两个簇中 所有样本对距离的平均值
agg = AgglomerativeClustering(linkage='ward',n_clusters=5).fit(X)

## 层次聚类没有聚类中心
plt.scatter(X[:,0],X[:,1],c=agg.labels_)
plt.show()

## 画个层次聚类的图
from scipy.cluster.hierarchy import linkage,dendrogram
def show_dendrogram(model):
    counts = np.zeros(model.children_.shape[0])
    n_samples = len(model.labels_)
    for i,merge in enumerate(model.children_):
        current_count=0
        for child_idx in merge:
            if child_idx < n_samples:
                current_count +=1    # leaf node
            else:
                current_count += counts[child_idx - n_samples]
        counts[i] = current_count

    linkage_matrix = np.column_stack(
        [model.children_,model.distances_,counts]
    ).astype(float)
    dendrogram(linkage_matrix)

show_dendrogram(agg)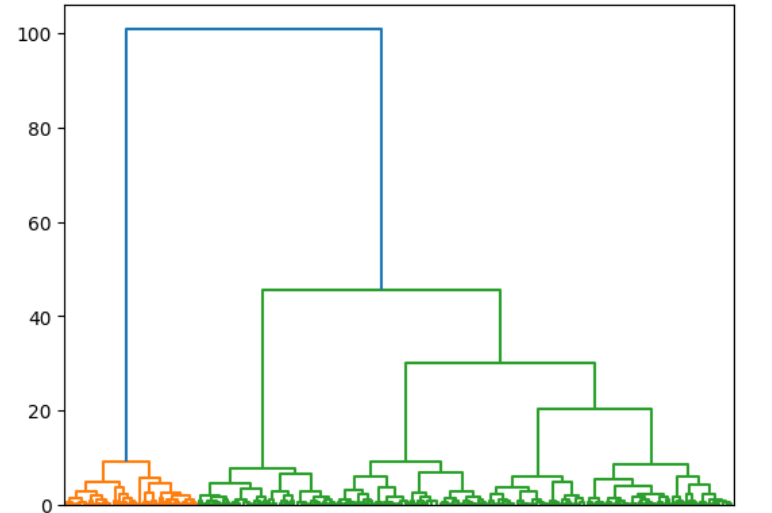

聚类评估

已知标签评价：

调整兰德指数
调整互信息分
V-Measure

未知标签评价：

轮廓系数
CHI

已知标签情况下：

python 复制代码

from sklearn.metrics import adjusted_rand_score
adjusted_rand_score(y,z)

from sklearn.metrics import adjusted_mutual_info_score
adjusted_mutual_info_score(y,z)

from sklearn.metrics import v_measure_score
v_measure_score(y,z)

ari_curve = []
ami_curve = []
vm_curve = []
clus = [2,3,4,5,6,7]
# 实验簇的不同值
for n_clusters in clus:
    clusterer = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
    z = clusterer.labels_
    ari_curve.append(adjusted_rand_score(y,z))
    ami_curve.append(adjusted_mutual_info_score(y,z))
    vm_curve.append(v_measure_score(y,z))

plt.plot(clus,ari_curve,label='ari')
plt.plot(clus,ami_curve,label='ami')
plt.plot(clus,vm_curve,label='vm')
plt.legend()
plt.show()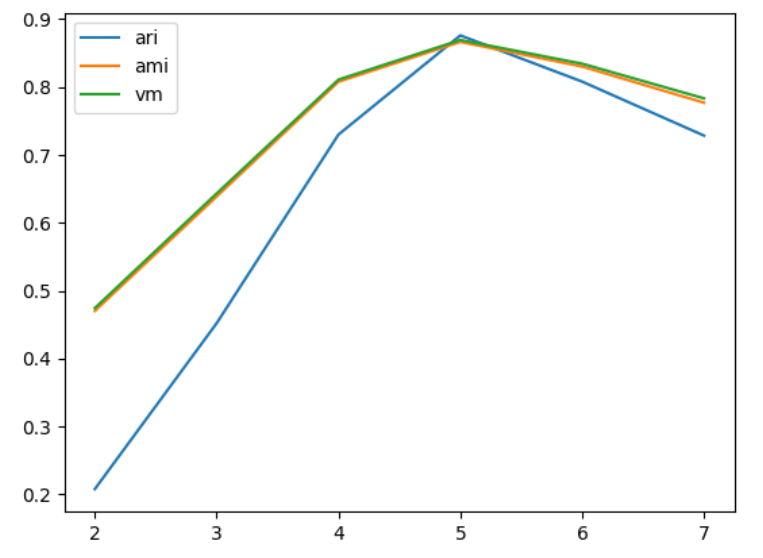

未知标签的情况下

python 复制代码

from sklearn.metrics import silhouette_score
kmeans =KMeans(n_clusters=5,random_state=0).fit(X)
cluster_labels = kmeans.labels_
si = silhouette_score(X,cluster_labels)


from sklearn.metrics import calinski_harabasz_score
calinski_harabasz_score(X,cluster_labels)

chi_curve = []
clus = [2,3,4,5,6,7]
for n_clusters in clus:
    clusterer = KMeans(n_clusters=n_clusters,random_state=0).fit(X)
    z = clusterer.labels_
    chi_curve.append(calinski_harabasz_score(X,z))

plt.plot(clus,chi_curve,label='chi')
plt.legend()
plt.show()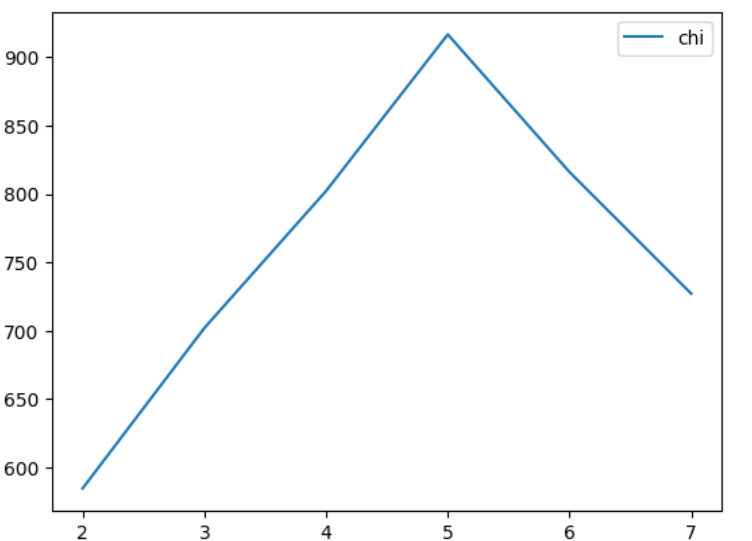

聚类算法的优缺点和适用条件

|---------|------------------------------------|------------------------------------------|----------------------------------------|
| | 优点 | 缺点 | 适用条件 |
| K-Means | 算法简单，收敛速度快簇间区别大时效果好对大数据集，算法可伸缩性强 | 簇数k难以估计对初始聚类中心敏感容易陷入局部最优簇不规则时，容易对大簇分割 | 簇是密集的、球状或团状簇与簇间区别明显簇本身数据比较均匀适用大数据集 |
| 分层聚类 | 距离相似度易定义限制少无需指定簇数可以发现簇的层次关系 | 对时间和空间需求大困难在于合并或分裂点的选择可扩展性差 | 适合于小型数据集的聚类可以在不同粒度水平上对数据进行探测，发现簇间层次关系 |