一、实验内容
2.5节 SAC算法算法在倒立摆上的表现
思考与要点记录:
① 策略梯度是用价值给策略背书(成王败寇),sac则是拿action分布下的期望给策略背书(集体大于个人)。
② 在最优动作不确定的某个状态下,熵的取值应该大一点;而在某个最优动作比较确定的状态下,熵的取值可以小一点。
③
价值训练:R + V 拟合Q
策略训练:熵 + Q 最大化
④ 重参数化技巧:将采样过程拆解为确定性计算 + 标准高斯噪声注入:噪声就是常数,把常数字和网络相乘就可以梯度计算。
⑤ SAC中的价值是网路是Q,没有用到V
二、实验目标
2.1 编码 SAC的 策略和价值网络
2.2 输出critic、actor loss以及收益变化曲线
三、实验过程
3.1 代码流程

3.2 策略网络
python
class PolicyNetContinuous(torch.nn.Module):
"""策略网络
输入状态,输出动作概率分布
"""
def __init__(self, state_dim, hidden_dim, action_dim, action_bound):
super(PolicyNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
self.fc_mu = torch.nn.Linear(hidden_dim, action_dim)
self.fc_std = torch.nn.Linear(hidden_dim, action_dim)
self.action_bound = action_bound
def forward(self, x):
"""输入状态state,输出动作 + 对数概率密度"""
x = F.relu(self.fc1(x))
# 重参数采样(高斯分布)
mu = self.fc_mu(x) # dim=1
std = F.softplus(self.fc_std(x)) # dim=1
dist = Normal(mu, std)
normal_sample = dist.rsample() # dim=1
# 分布非线性压缩与概率转化
log_prob = dist.log_prob(normal_sample)
action = torch.tanh(normal_sample)
# 计算在新分布中的对数概率密度
log_prob = log_prob - torch.log(1 - torch.tanh(action).pow(2) + 1e-7)
# 动作现行放缩(不改变概率)
action = action * self.action_bound
# 输出动作,以及动作的对数概率密度
return action, log_prob3.3 价值网络
python
class QValueNetContinuous(torch.nn.Module):
"""价值网络
输入状态,输出价值估计
"""
def __init__(self, state_dim, hidden_dim, action_dim):
super(QValueNetContinuous, self).__init__()
self.fc1 = torch.nn.Linear(state_dim + action_dim, hidden_dim)
self.fc2 = torch.nn.Linear(hidden_dim, hidden_dim)
self.fc_out = torch.nn.Linear(hidden_dim, 1)
def forward(self, x, a):
cat = torch.cat([x, a], dim=1)
x = F.relu(self.fc1(cat))
x = F.relu(self.fc2(x))
return self.fc_out(x)3.4 模型迭代
python
def update(self, transition_dict):
states = torch.tensor(transition_dict['states'],
dtype=torch.float).to(self.device)
actions = torch.tensor(transition_dict['actions'],
dtype=torch.float).view(-1, 1).to(self.device)
rewards = torch.tensor(transition_dict['rewards'],
dtype=torch.float).view(-1, 1).to(self.device)
next_states = torch.tensor(transition_dict['next_states'],
dtype=torch.float).to(self.device)
dones = torch.tensor(transition_dict['dones'],
dtype=torch.float).view(-1, 1).to(self.device)
# 和之前章节一样,对倒立摆环境的奖励进行重塑以便训练,奖励归一化
rewards = (rewards + 8.0) / 8.0
# 更新两个Q网络
td_target = self.calc_target(rewards, next_states, dones) # 计算目标网络
critic_1_loss = torch.mean(
F.mse_loss(self.critic_1(states, actions), td_target.detach()))
critic_2_loss = torch.mean(
F.mse_loss(self.critic_2(states, actions), td_target.detach()))
self.critic_1_optimizer.zero_grad() #
critic_1_loss.backward()
self.critic_1_optimizer.step()
self.critic_2_optimizer.zero_grad()
critic_2_loss.backward()
self.critic_2_optimizer.step()
# 更新策略网络
new_actions, log_prob = self.actor(states) # 动作 + 熵
entropy = -log_prob # 对数概率是正值
q1_value = self.critic_1(states, new_actions)
q2_value = self.critic_2(states, new_actions)
# 含义1:最大化Q,这是模型收敛必须要求的,然后传递到策略网络对动作(均值和方差)的选取,尽量选择最好的动作
# 含义2:最大化动作熵,也就是最小化对数概率密度,也就是最小化概率,也就是打压当前动作的概率密度。
# 两者相反想成,最大化Q理论上会让动作更加集中明确,而最大话熵会让动作更加不确定。
actor_loss = torch.mean(-self.log_alpha.exp() * entropy -
torch.min(q1_value, q2_value))
self.actor_optimizer.zero_grad()
actor_loss.backward() # 执行策略反向传播,整个链条都会有梯度,但是只会给actor更新,因为只有actor的参数优化器执行了step动作。
self.actor_optimizer.step()
# 更新alpha值(就要熵和目标熵之间的距离更新熵的权重)
alpha_loss = torch.mean(
(entropy - self.target_entropy).detach() * self.log_alpha.exp())
self.log_alpha_optimizer.zero_grad()
alpha_loss.backward()
self.log_alpha_optimizer.step()
self.soft_update(self.critic_1, self.target_critic_1)
self.soft_update(self.critic_2, self.target_critic_2)四、实验结果
结论先行:
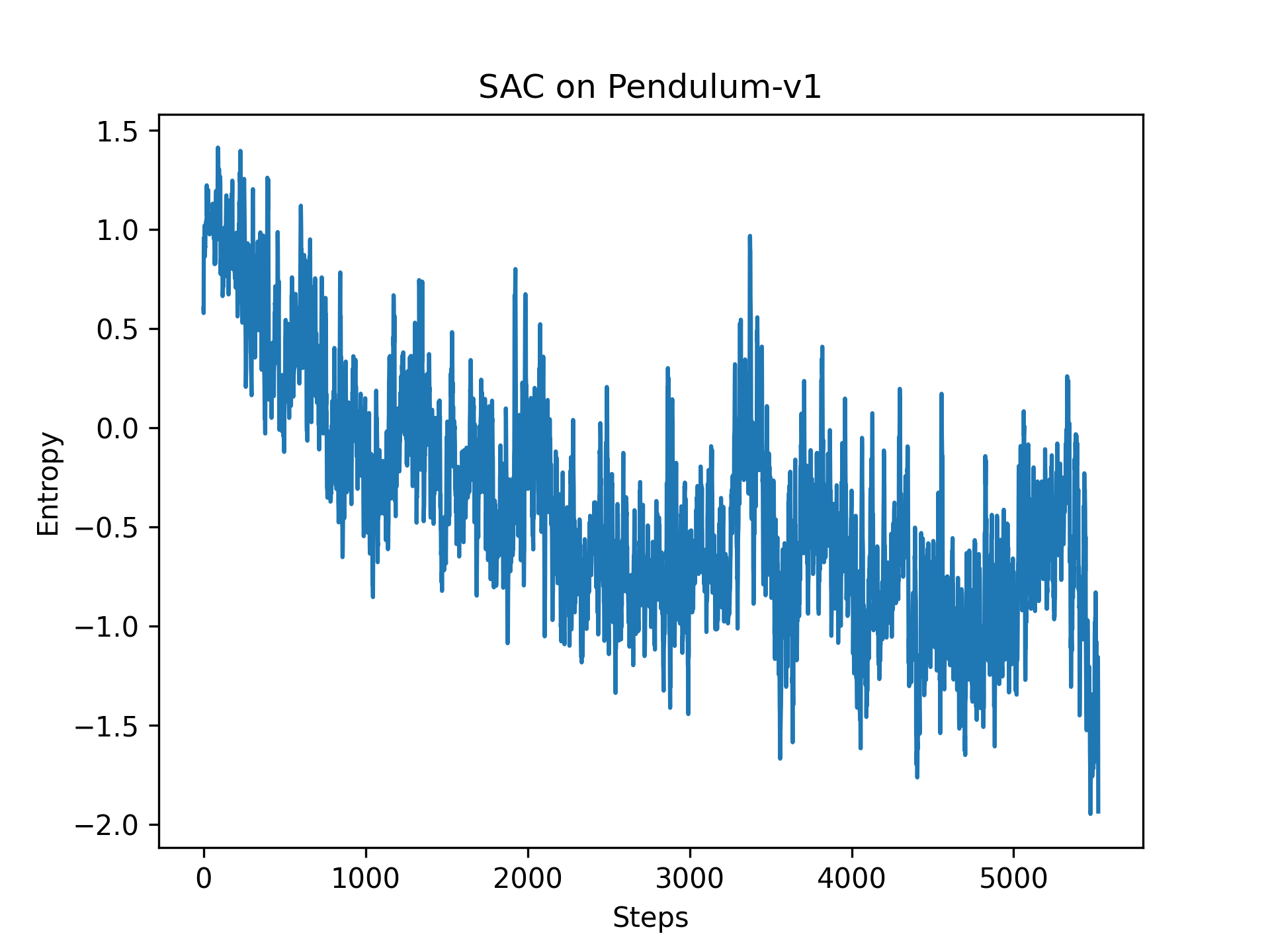
① 熵逐渐降低,最终稳定在目标熵(-1,其中1是自由度)附近。注意这里的熵是微分熵,不是香农熵(非负)
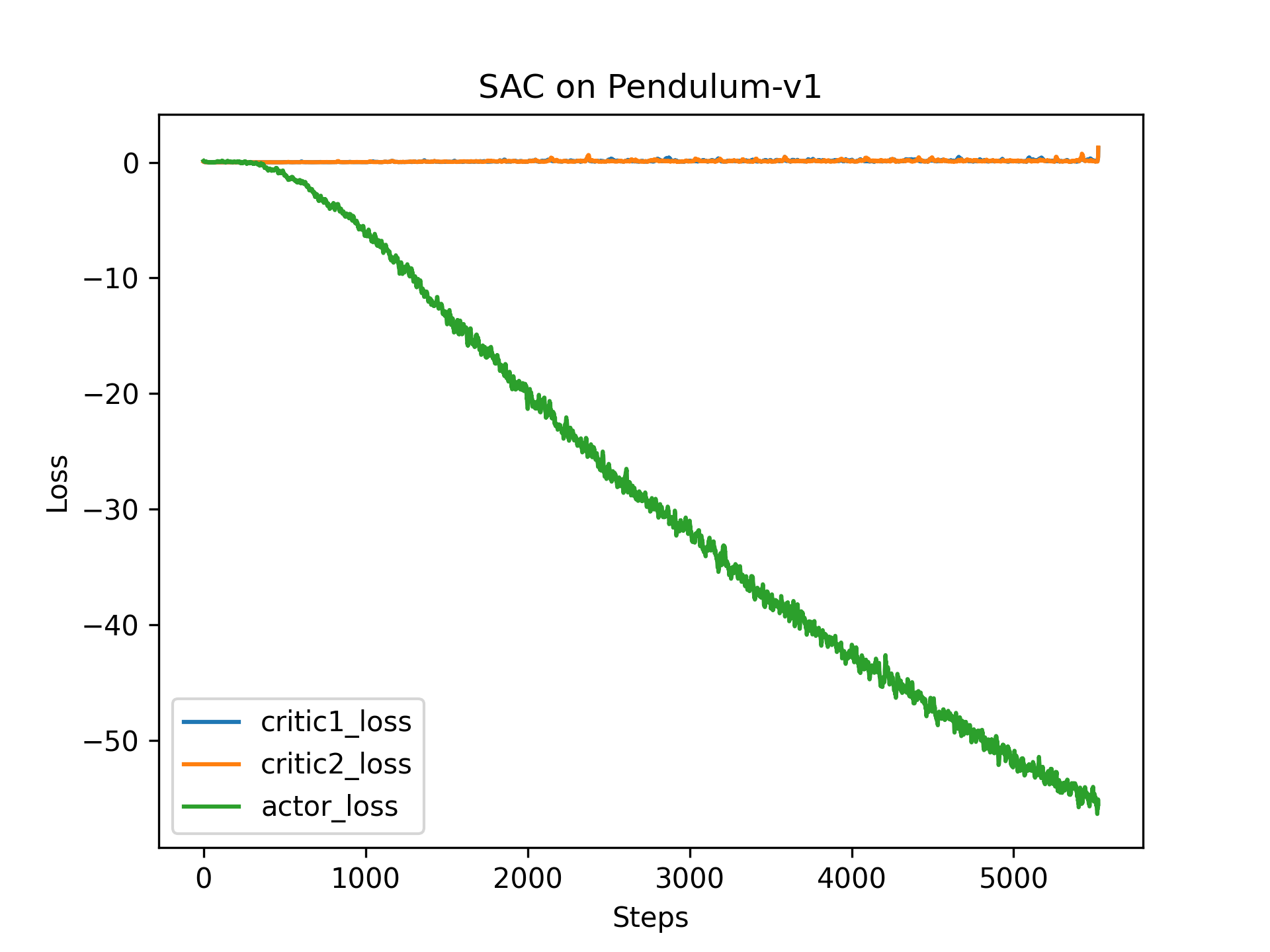
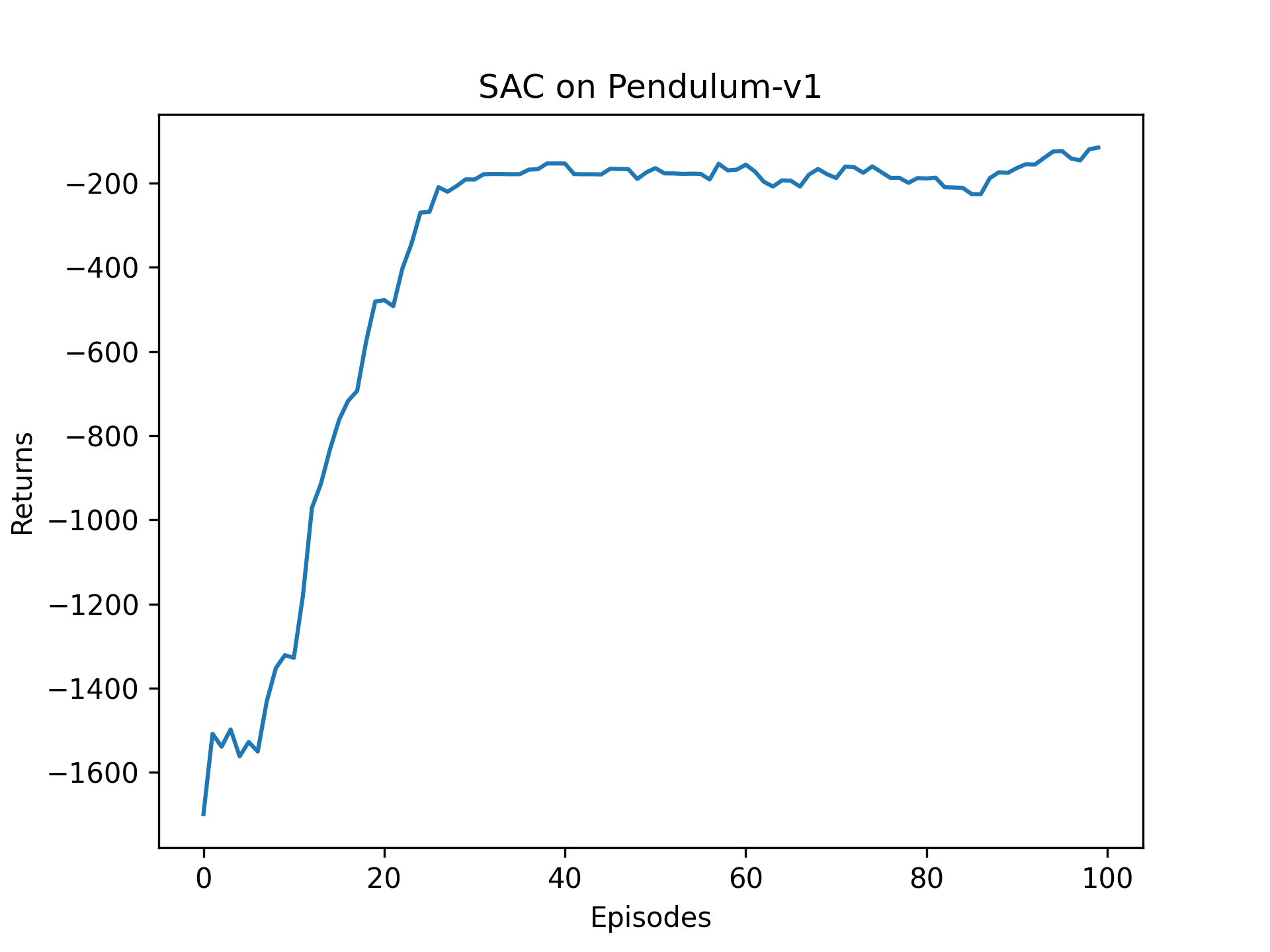
② critci迅速收敛,actor_loss持续下降,但是回报收敛到-200(长度为200,相当于平均回报=-1,已经比较大了)
附录

倒立摆的奖励计算
