【C++】并查集&家谱树

[洛谷 P1551 亲戚](#洛谷 P1551 亲戚)

题目背景

题目描述

输入格式

[洛谷 P14077 [GESP202509 七级] 连通图](#洛谷 P14077 [GESP202509 七级] 连通图)

洛谷 P1551 亲戚

题目背景

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。

题目描述

规定：x 和 y 是亲戚，y 和 z 是亲戚，那么 x 和 z 也是亲戚。如果 x，y 是亲戚，那么 x 的亲戚都是 y 的亲戚，y 的亲戚也都是 x 的亲戚。

输入格式

第一行：三个整数 n,m,p，（n,m,p≤5000），分别表示有 n 个人，m 个亲戚关系，询问 p 对亲戚关系。

以下 m 行：每行两个数 Mi，Mj，1≤Mi, Mj≤n，表示 Mi 和 Mj 具有亲戚关系。

接下来 p 行：每行两个数 Pi,Pj，询问 Pi 和 Pj 是否具有亲戚关系。

输出格式

p 行，每行一个 Yes 或 No。表示第 i 个询问的答案为"具有"或"不具有"亲戚关系。

输入输出样例

输入 #1

复制代码

输出 #1

复制代码

Yes
Yes
No

并查集

上面的题就是并查集的板子。我们仍然先抛开它不谈，讲讲并查集。

并查集，顾名思义，"并"就是合并，"查"就是查询。首先先讲定义。

定义

在下文中，我们定义：

fa[i] 为 i 的父亲。

find(i) 的值是 i 的祖先（不只是它的父亲，是它父亲的父亲......也就是根）。

思路

如何判断 i 和 j 是否是亲戚？根据上文的定义，我们知道 find(i) 是 i 的祖先。那么判断 i 和 j 是否是亲戚，只需要看他们的祖先是否是一个人就行了。生活常识，如果两个人的祖先一样，那他们就是亲戚。

既然关键在这里，那么 find 函数又该怎么实现呢？接下来，我们讲并查集的"并"。

"并"

用 find 函数来实现"并"，首先它的参数为 x，表示需要返回 x 的祖先。

如何找到一个节点的祖先？是的，找到它的父亲，然后是父亲的父亲......直到找到某位父亲，其没有父亲即可。这个节点就是祖先。

这个反复往上"找父亲"的过程，很容易让人想到递归。

x 的父亲是 fa[x]，fa[x] 的父亲是 fa[fa[x]]......如何判断一个节点没有父亲呢？初始化时，我们将所有节点的父亲都设置成它自己。（在输入的时候给它真正的父亲，若没有，则代表它是一个祖先）

cpp 复制代码

for(int i=1;i<=n;i++)
    fa[i]=i;

所以如果它的 fa（父亲）是它自己，那么它就是祖先。我们找到了递归的出口。

反之，如果它有父亲呢？

往上跳（递归），直到跳到出口（祖先）。

所以 find 函数（找祖先）的代码：

cpp 复制代码

int find(int x) {
    if(fa[x]==x)
        return x;//祖先的编号（自己）
    else
        return fa[x];//往上跳
}

路径压缩

想一下，每一次查询，都要往上跳一遍，非常浪费时间。而且"并"的过程似乎没有体现出来。

如何让查询的时间变少呢？

我们会发现，其实 fa[i] 是不重要的，i 的父亲只是作为中介来寻找祖先；重要的是 i 的祖先。所以，这棵家族的树结构也是不重要的。

我们的目标是，能够保证一次就跳到祖先。

举个例子。对于原来的一棵"家谱树"：（父亲节点表示父亲，子节点表示孩子）

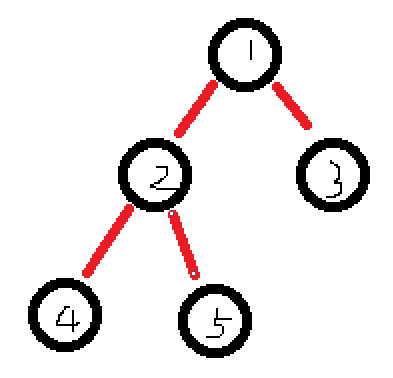
我们更改树结构为：

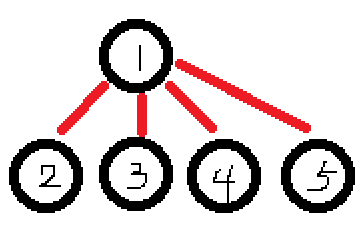
仔细想想，这样的结构并不影响最终的结果，这里不再赘述，如果仍然不懂，请在评论区指出。

这个过程叫做"路径压缩"。

更改 find 函数的代码，解释见注释：

cpp 复制代码

int find(int x) {
	if(fa[x]==x)
		return x;
	else
		return fa[x]=find(fa[x]);
		/*这句话相当于
		fa[x]=find(fa[x]);
		return fa[x];
		*/
	//使得 x 的父亲变成了 x 的祖先
}

构建树

为什么是树？因为父亲和孩子的关系就是树结构，下同。

假设有点 u 和点 v，要将它们合并。

这里比较简单，上代码，注释在关键的地方有解释。

cpp 复制代码

void un(int u,int v) {
	//找到 u 和 v 各自的祖先
	int rootu=find(u);
	int rootv=find(v);
	
	if(rootu!=rootv) {//它们不在同一家族
		fa[rootv]=rootu;
		//v 的祖先变成，u 祖先的儿子
	}
}

图示：（红色为新添加的边）

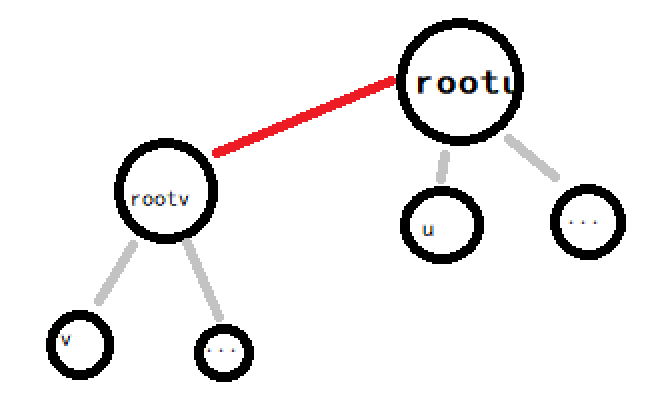
"查"

前面也提到了，如果 i 和 j 是亲戚，那么他们有着一样的祖先。它们的祖先分别是 find(u) 和 find(v)。

判断它们是否为亲戚，直接检查其祖先是否相同即可。代码：

cpp 复制代码

if(find(u)==find(v))
	cout<<"Yes"<<endl;
else 
	cout<<"No"<<endl;

代码

分布的实现已经完成，接下来将它们拼接到一起。

回到题目【P1551 亲戚】。AC记录。

cpp 复制代码

#include<iostream>
using namespace std;
int n,m,p,fa[5002];

int find(int x) {
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}//找祖先

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);//快读快写

	cin>>n>>m>>p;

	for(int i=1;i<=n;i++)
		fa[i]=i;//初始化

	for(int i=0,a,b;i<m;i++) {
		cin>>a>>b;
		fa[find(b)]=find(a);
	}//合并

	while(p--) {
		int i,j;
		cin>>i>>j;
		if(find(i)==find(j))
			puts("Yes");
		else 
            puts("No");
	}
	return 0;
}

求连通块

洛谷 P14077 [GESP202509 七级] 连通图

题目描述

给定一张包含 n 个结点与 m 条边的无向图，结点依次以 1,2,...,n 编号，第 i 条边（1≤i≤m）连接结点 ui 与结点 vi。如果从一个结点经过若干条边可以到达另一个结点，则称这两个结点是连通的。

你需要向图中加入若干条边，使得图中任意两个结点都是连通的。请你求出最少需要加入的边的条数。

注意给出的图中可能包含重边与自环。

输入格式

第一行，两个正整数 n,m，表示图的点数与边数。

接下来 m 行，每行两个正整数 ui,vi，表示图中一条连接结点 ui 与结点 vi 的边。

输出格式

输出一行，一个整数，表示使得图中任意两个结点连通所需加入的边的最少数量。

输入输出样例

输入 #1

cpp 复制代码

输出 #1

cpp 复制代码

输入 #2

cpp 复制代码

输出 #2

cpp 复制代码

这里是我单独写的一篇题解：《连通图【求联通块】小白》

现在明白了取名的智慧，起得短一点点了......。......

解法

这是比较经典的问题了。求出要添加多少条边，就是问有多少连通块。

一个连通块就有一棵类似树的结构，有多少祖先就有多少连通块，最后减一即可。详细见上文提到的题解。求祖先数量就是并查集啦。

AC记录。

cpp 复制代码

#include<iostream>
#include<vector>
using namespace std;

int m,n;
int fa[100005];

int find(int x) {
	if(fa[x]!=x) fa[x]=find(fa[x]);
	return fa[x];
}

void add(int x,int y) {
	int roox=find(x),rooy=find(y);
	if(roox!=rooy)
		fa[rooy]=roox;
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		fa[i]=i;
	for(int i=0;i<m;i++) {
		int u,v;
		cin>>u>>v;
		add(u,v);
	}
	
	int cnt=0;
	for(int i=1;i<=n;i++) {
		if(fa[i]==i)//父亲是自己，就是祖先
			++cnt;
	}
	cout<<cnt-1;
	return 0;
}

相似题

连通块相似题：洛谷 P1536 村村通（偶然发现的，差不多）。

模板题：P3367 【模板】并查集。

写在最后

结尾有点匆忙，来不及了。很高兴遇见你，我们下次再见。

希望你能留下一个赞，谢谢。仅此奢求。

如果有问题、错误，请在评论区指出，谢谢。