坐标系知识概述

坐标系知识概述

坐标系是一套规则，用来明确地确定一个点在空间中的位置。

在工程应用领域，坐标系会根据具体场景的需求，对纯数学坐标系进行针对性调整（针对特定领域问题优化）。核心逻辑是：数学坐标系是通用、抽象的工具，而工程坐标系需要贴合实操场景、简化计算、降低误差，因此会在原点位置、轴方向定义等方面进行适配性修改。

可以将坐标系的世界分为两大阵营：数学理论界（教科书标准）与 工程应用界（编程、图形学）。

一、数学（包括物理学）坐标系

常见类型

1. 一维坐标系：数轴

• 构成 ：一条直线（基准线）、一个原点 （0点）、一个正方向 （通常向右）、一个单位长度。
• 如何定位：用一个数字（坐标）即可。例如：点A的坐标是 3，表示它在原点右侧3个单位处；点B的坐标是 -2，表示它在原点左侧2个单位处。
• 关键思想 ：建立了直线上的点与实数的一一对应关系。

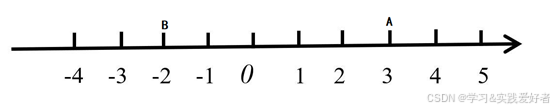
2. 二维坐标系：平面坐标系

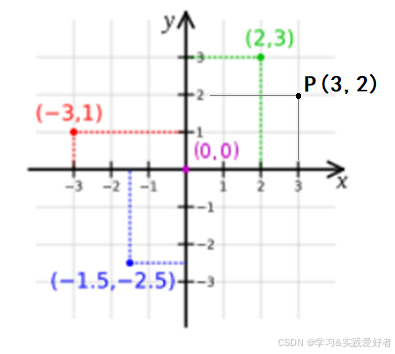
(1) 直角坐标系（笛卡尔坐标系）

• 构成 ：两条互相垂直、相交于原点的数轴。
  • x 轴（横轴）：水平，向右为正。
  • y 轴（纵轴）：垂直，向上为正。
• 如何定位 ：用一对有序数字 (x, y) 表示。
  • x 坐标（横坐标） ：点到y轴的水平距离（带方向）。
  • y 坐标（纵坐标） ：点到x轴的垂直距离（带方向）。
• 例子：点P (3, 2) 表示从原点向右3个单位，再向上2个单位。
• 核心应用：函数图像、平面几何、计算机屏幕像素定位（屏幕左上角为原点(0,0)是特例）。

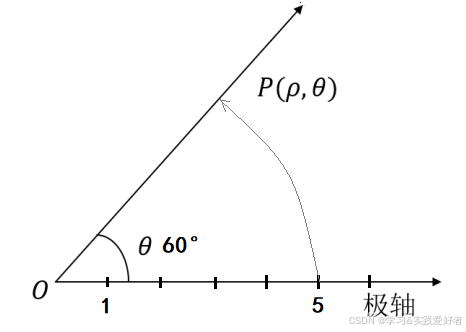
(2) 极坐标系

• 构成 ：一个极点 （相当于原点）、一条极轴（从极点出发的基准射线，通常水平向右）。
• 如何定位 ：用一对 (ρ, θ) 表示。
  • 极径 (ρ) ：点到极点的距离（ρ ≥ 0）。
  • 极角 (θ) ：从极轴到该点连线（极径）所转过的角度（通常以弧度或度为单位，逆时针为正）。
• 例子：点P (5, 60°) 表示在距离极点5个单位，且与极轴夹角为60°的方向上。

• 核心应用：描述圆形、旋转、有中心辐射状的事物（如雷达、卫星天线、艺术图案）。
• 与直角坐标的转换：

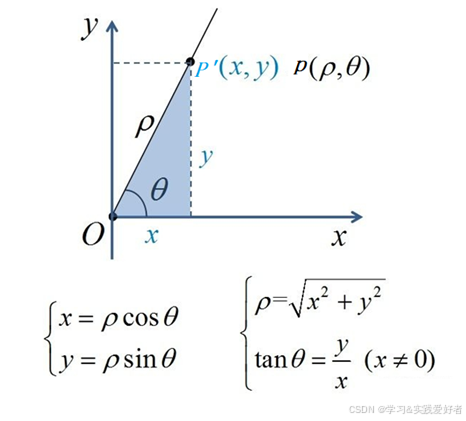
3. 三维坐标系：空间坐标系

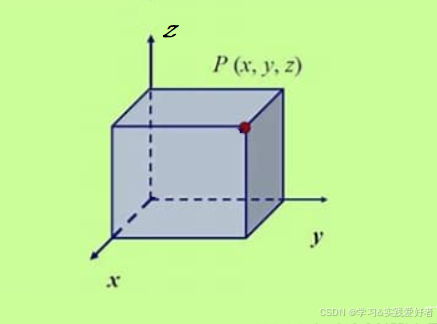
(1) 三维直角坐标系（空间直角坐标系）

• 构成 ：三条两两垂直、相交于原点的数轴（x轴, y轴, z轴）。符合右手定则（右手食指朝x轴，中指朝y轴，拇指方向就是z轴正方向，见后面手性部分）。
• 如何定位：用三元组 (x, y, z) 表示。
• 例子：房间角落的一个点，可以用它到两面墙和地面的距离来确定。

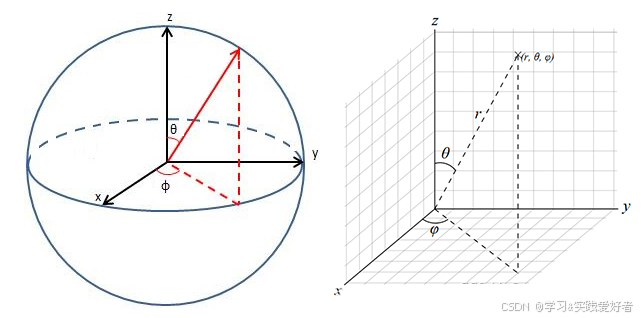
(2) 球坐标系

• 思想：用距离和两个角度定位空间点，像地球的经纬度。
• 如何定位 ： (r, θ, φ)（不同领域符号习惯不同，此为物理常用）
  • r ：点到原点的距离。
  • θ ：点与z 轴正方向的夹角（天顶角）。
  • φ ：点在xOy平面上的投影与x 轴正方向的夹角（方位角）。
• 例子：GPS定位（经度、纬度、海拔高度就是球坐标的一种变体）、描述原子中电子的位置。点P(7, 30°, 60°)表示距离原点7，与z轴夹角30°，在xoy平面上的投影与x轴夹角60°

• 与三维直角坐标的转换 ：
  • x = r * sinθ * cosφ
  • y = r * sinθ * sinφ
  • z = r * cosθ

上面介绍的数学中的坐标系，这是所有坐标理论的源头。

二、工程应用界（编程、图形学）

图形学编程场景下的坐标系知识，这和纯数学坐标系示右区别的。

（一）、屏幕坐标系

一般采用：原点在左上角、Y 轴向下、单位为像素，所有 2D 绘制 / 鼠标交互都基于此。相关内容可见：计算机屏幕坐标系简介 https://blog.csdn.net/cnds123/article/details/144533246

（二）、3D 图形学坐标系

3D 图形学需区分左手 / 右手坐标系，其 Z 轴方向直接影响旋转、投影的计算逻辑。

下面重点介绍3D 图形学坐标系。

先了解核心概念基础

1. 基础之一：手性 (Chirality) ------ 左手 vs 右手

这是坐标系的"基因"，决定了由前两个轴确定第三个轴方向的规则（叉乘法则）。

• 右手系 (Right-Handed)
  • 判定法：伸出右手，四指从 X 轴转向 Y 轴，大拇指指向即为 Z 轴。
  • 地位：数学、物理学的绝对标准；OpenGL、Blender 采用。
• 左手系 (Left-Handed)
  • 判定法：伸出左手，做同样的动作。
  • 地位：DirectX、Unity、Unreal Engine、Web 前端习惯采用。

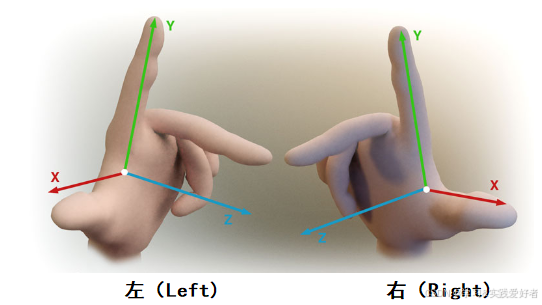
图示记忆：

• 右手：大拇指(X)、食指(Y)、中指(Z) 互相垂直。
• 左手：同样的姿势，Z 轴方向与右手刚相反。

2. 基础之二：谁是" 上" (Up Axis)

这是坐标系的"站姿"。

• Z-Up ：Z 轴朝天 。来源于建筑绘图习惯（XY是地面图纸，Z是楼高）。
  • 代表：数学课本、Blender 、3ds Max 、Unreal 。
• Y-Up ：Y 轴朝天 。来源于屏幕观察习惯（XY是屏幕平面，深度变为了Z）。
  • 代表：OpenGL 、Unity 、Maya 。
• Y-Down ：Y 轴朝地 。来源于阅读习惯（从左上角开始阅读，往下行数增加）。
  • 代表：2D Canvas 、SVG 、网页 CSS 、p5.js 。

编程与图形学中的坐标系 (工程应用界)，这里有些混乱，因为不同的厂商制定了不同的标准。将最主流的系统总结如下：

1. 建模与工业设计流派 (Z-Up 右手)

沿用了数学和建筑学的习惯。

• 代表软件 ：Blender 、3ds Max 、AutoCAD。
• 配置 ：
  • X：右 (+)
  • Y ：后/里 (+) 或 前 (+) ------ 各软件定义" 前" 有歧义，但 Y 都在水平面上
  • Z：上 (+)
  • 手性：右手系。

2. 传统图形学与影视流派 (Y-Up 右手)

这是 OpenGL 定义的行业标准，影响了早期的图形工作站和 Maya。

• 代表软件 ：OpenGL (World Space)、Maya 、Godot。
• 配置 ：
  • X：右 (+)
  • Y：上 (+)
  • Z ：向外 / 朝向观察者 (+) ------ 注意：这意味着看向屏幕深处是 Z 的负方向。
  • 手性：右手系。

3. 当代游戏引擎流派 (Y-Up 左手)

为了让 Z 轴正方向代表"前方"（符合直觉），DirectX 和 Unity 选择了左手系。

• 代表软件 ：Unity 、Microsoft DirectX 、Ursina。
• 配置 ：
  • X：右 (+)
  • Y：上 (+)
  • Z ：向前 / 朝向屏幕里 (+) ------ 这符合" 前进" 的直觉。
  • 手性 ：左手系。

4. 网页与 2D 延伸流派 (Y-Down 左手)

这是为了兼容网页排版习惯（原点在左上角）。

• 代表软件 ：p5.js (WebGL) 、HTML Canvas 、SVG。
• 配置 ：
  • X：右 (+)
  • Y ：下 (+) ------ 这是最大的特征。
  • Z ：向外/朝向观察者 (+) ------ 这是为了保持Z 轴正方向是" 近大远小"。
  • 手性 ：左手系。

总结表

以"你的头顶"和"你的脸"为参照物，总结各系统的轴向正方向 (+)：

领域/ 系统	X 轴 (+)	Y 轴 (+)	Z 轴 (+)	坐标系类型	典型代表
纯数学	前	右	上 ( 头顶)	右手 Z-Up	教科书
建模	右	后/里	上 ( 头顶)	右手 Z-Up	Blender
图形标准	右	上 ( 头顶)	后 ( 向外)	右手 Y-Up	OpenGL, Maya
游戏引擎	右	上 ( 头顶)	前 ( 进屏幕)	左手 Y-Up	Unity, DirectX
网页 3D	右	下 ( 脚底)	后 ( 向外)	左手 Y-Down	p5.js, Web2D

要建立起相关坐标系统正确的空间感知，需要思考两个问题："谁朝上？" 和 "伸左手还是右手？"。大拇指（x）、食指（y）、中指（z）。注意："手性"（Chirality）可以用来帮助确定三个轴之间的相对关系，而不是确定轴在这个世界里的绝对朝向。

附录

坐标系交互演示 https://www.mathsisfun.com/data/cartesian-coordinates.html

Python + Ursina设计3D小游戏 https://blog.csdn.net/cnds123/article/details/155709276