目的
1、为避免一学就会、一用就废,这里做下笔记
2、上文已讲明卷积的概念,这里继续说明何为"神经网络"
基础要求
1、了解矩阵的基本知识
2、了解机器学习的基本概念
是什么:何为神经网络(Neural Network)
定义
1、神经网络是一种算法框架,该算法框架用来构建类似生物神经网络结构的计算模型。
2、构建好的模型通过网络中的大量参数,存储输入样本的特征,然后可以用该模型对新的样本做预测
Q1:参数存在神经网络的哪里?
A1:神经网络由点(神经元)和线分层连接构成,参数存在线上
Q2:训练模型就是调这些线上的参数吗?
A2:是,但不完整。除了用数据自动化调这些线上的参数,还需要工程师结合经验和实践,人工调整一些超参数:网络的层数、每层的神经元数等
Q3:到底怎么从根本上理解神经网络是什么呢?
A3:重点了解其数学模型和计算模型,见下一节↓
数学模型
神经网络的数学模型如下:
y = f ( x ) = σ n ( W n . . . σ 2 ( W 2 ∗ σ 1 ( W 1 ∗ x + b 1 ) + b 2 ) . . . + b n ) y=f(x) = σ_n(Wₙ ... σ_2(W₂ * σ_1(W₁ * x + b₁) + b₂) ... + bₙ) y=f(x)=σn(Wn...σ2(W2∗σ1(W1∗x+b1)+b2)...+bn)
数学模型说明:
| 符号 | 说明 |
|---|---|
| x | 原始输入信号,一般是一个N维向量,如三维向量[1, 2, 3] |
| y | 预测输出信号,也是一个向量,向量的维度由工程师视具体问题设定。如二分类时,可以输出一维向量,以直接给出是哪个分类;或者输出二维向量,给出不同分类的概率值 |
| W n W_n Wn | 第n层的参数矩阵,该矩阵行数为该层神经元数 d n d_n dn,列数为该层输入信号的维度数(即上一层神经元数) d n − 1 d_{n-1} dn−1。注意:每一层的神经元数,是工程师视经验人为设定,属于超参数,数学公式中没有体现 |
| b n b_n bn | 转置参数,作用和 W n W_n Wn类似,是一个 d n d_n dn维的向量 |
| σ n ( x ) σ_n(x) σn(x) | 第N层的激活函数,一般输入和输出都是一个浮点数,且除了最外层要根据目标场景定制选择激活函数,内部各层(即隐藏层)的激活函数都相同。如 σ ( x ) = m a x ( 0 , x ) σ(x)=max(0,x) σ(x)=max(0,x) |
模型的训练过程,就是给该模型大量输入标识好的样例数据,通过监督学习,使用反向传播算法,让模型不断自动调整参数,使得最终模型整体的预测效果能达到预期标准
计算模型
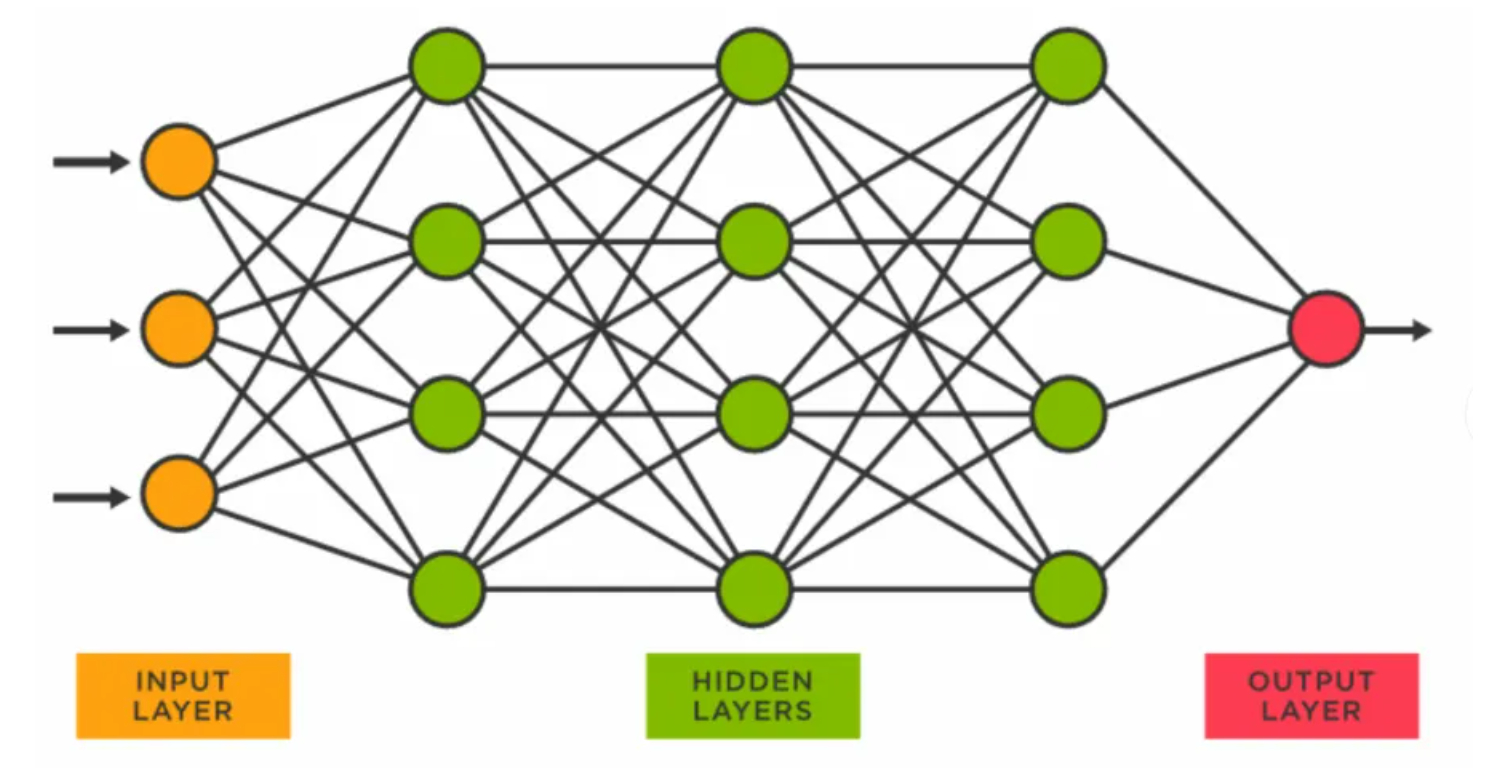
1、模型分为输入层、隐藏层、输出层
2、每个点是一个神经元,每个神经元存储一个浮点数
3、每个神经元收到信号后,会对信号进行处理,该处理函数称为激活函数 σ ( x ) σ(x) σ(x)
4、每根线是一个数学运算, W j i ∗ x i + b j W_{ji}*x_i+b_{j} Wji∗xi+bj,注意:对单个神经元而言,它所有输入线的信号累加在一起才是该神经元的一个完整输入信号(一个浮点数),而不是几根输入线代表几个输入信号
5、模型的总层数,以及每一层的神经元数,属于超参数,由工程师结合经验和实践人为设定,业界会给出不同类型问题适合层数的参考
6、一般输入层和隐藏层使用相同的激活函数,输出层的激活函数,需要视模型的具体预测目标做选择
为什么
AI领域的神经网络,哪里模仿了生物神经网络?
| 生物神经网络 | AI神经网络 | 说明 | |
|---|---|---|---|
| 形状相似 | 通过大量神经元细胞和连接组织(树突、轴突等)相互连接形成。可简化为大量点和线组成的三维网状结构 | 也是由大量点和线连接组成的类网状结构,准确讲是二维层级结构 | 结构上粗浅模仿,AI为计算方便选择层级结构 |
| 点 | 神经元细胞,它能对输入的信号进行简单处理,并传递给其他神经元 | 也叫神经元,能对输入的数据进行简单处理,处理规则就是激活函数σ(x) | 高度模仿并补充细节:AI神经网络中,一个输入信号传递到单个神经元就是一个浮点数,该值经σ(x)处理后变成另一个浮点数。某一层所有N个神经元存储的数字合在一起是一个N维向量 |
| 线 | 树突、轴突等组织是线,用来接收并传递信号。且传递过程,信号会有所衰减 | 参数矩阵是线,且不是一条线,而是MN条线。上层输入信号(M维向量)通过和参数矩阵点乘运算,输出一个N维向量。中间的计算次数是MN,N维向量中的每个维度值是浮点数,这些浮点数就是传递给每个神经元的输入信号 | 高度模仿并补充细节:AI神经网络中,通过对输入的M维向量进行矩阵运算,来传递信号。并通过线性计算规则( f ( x ) = w x + b f(x)=wx+b f(x)=wx+b)来模拟原始信号的衰减 |
神经网络,是算法还是模型?
- 算法规定了计算的步骤、数据加工转换的方法,类似菜谱
- 模型是算法调整好参数后的产出物,用来后续预测,类似炒出来的菜
- 神经网络一词多义,它既是算法,也是模型,或者更准确说是算法框架。
1)算法部分:神经网络定义了完整的计算流程,包括前向传播如何计算输出、反向传播如何更新权重、梯度下降如何优化参数。这些具体的数学步骤和更新规则构成了神经网络的算法部分。
2)模型部分:训练完成后得到的权重矩阵和偏置向量(即参数集合)就是模型本身。这个参数化的数学函数能够对新的输入数据进行预测,是算法学习后得到的最终产物
神经网络,与机器学习、深度学习的关系?
- 神经网络,是机器学习的范畴,是其中的一种算法框架。除此之外,机器学习还有大量其他算法框架:决策树算法、线性回归算法、逻辑回归算法等
- 深度学习,是机器学习的研究分支,它完全基于神经网络算法框架。没有神经网络,就没有深度学习。深度学习的深度,指神经网络的层数较多。但具体多少层算深度学习,并无标准。为简单理解,1-3算浅层,4-10算中层,10以上算深层
为什么神经网络,尤其是深度学习中的多层神经网络,比传统ML算法更具智能?
神经网络本质上是一个万用函数逼近器,其结构赋予它两种关键能力:
- 拟合极度复杂的非线性关系
1)现实世界的规律(如图像到类别、语音到文字、围棋棋盘到最佳落子点)是高度非线性且复杂的。
2)浅层模型(如逻辑回归、SVM)拟合复杂函数的能力有限。
3)深度神经网络通过多个非线性层的堆叠,可以构造出极其复杂的复合函数,从而能够刻画现实中那些"只可意会,难以用规则描述"的映射关系。 - 灵活的关系与结构建模 :
1)卷积神经网络(CNN):天然具有平移不变性和局部连接的假设,完美契合图像、语音等网格化数据的空间/局部关系。
2)循环神经网络(RNN) 和 Transformer:具有记忆或注意力机制,能处理和理解序列数据(如语言、视频)中元素间的长程依赖关系。
3)图神经网络(GNN):能直接处理非欧几里得数据(如社交网络、分子结构),学习实体间的关系。
4)这种针对数据结构量身定制的归纳偏置,让神经网络能更"智能"地理解数据的内在联系
神经网络的弊端在哪里?
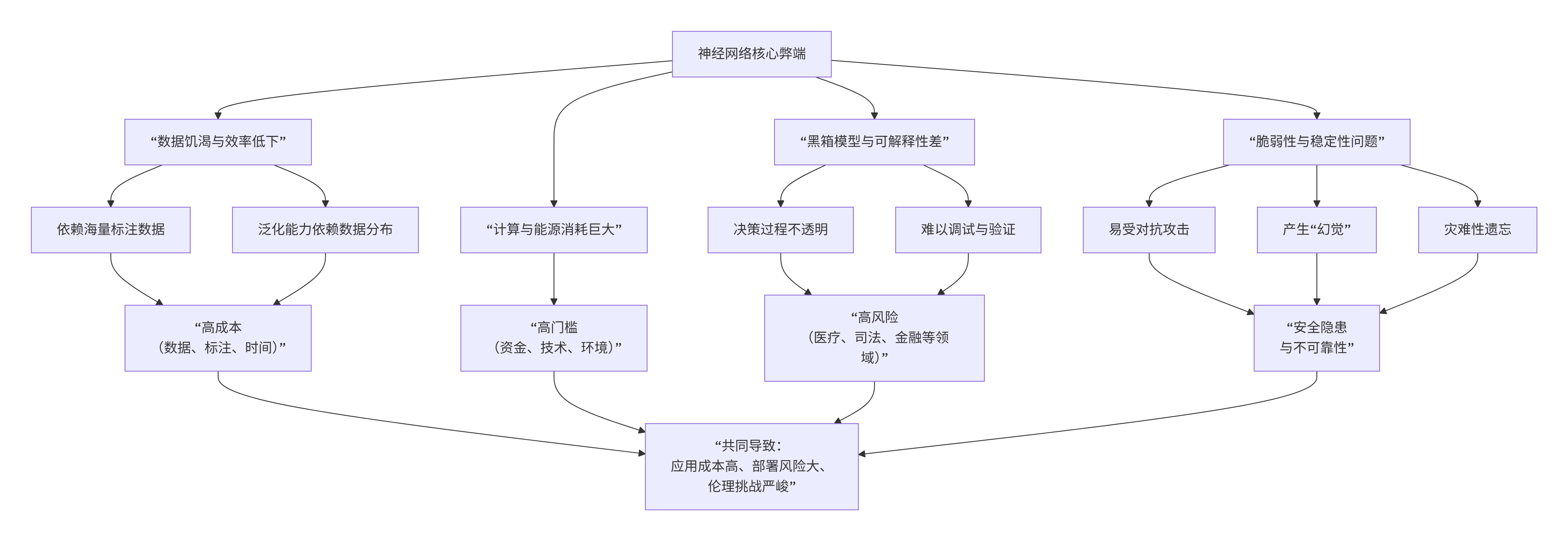
怎么办?
同机器学习一样,神经网络也分模型训练 和部署使用 两个阶段。这里重点讲下模型训练 阶段的核心调参环节。
调参环节,是"前向传播 → 损失评估 → 反向传播 → 更新参数 "流程的循环,直到损失达到最小
三个核心步骤:
- 前向传播
给定神经网络模型一套初始参数,让训练集中的数据从输入层计算到输出层,这个过程就是前向计算(或称"向前计算")。 - 损失评估
前向计算的输出,是当前参数下,模型对训练集中原始数据给出的预测结果。损失评估就是将这个预测结果和真实结果(人工判断并标注)进行比较,以评估模型预测的准确性,这里会用到损失函数 - 反向传播
这是算法的核心。目标是回答:"损失函数对于网络中每一个参数(每一个W和b)的微小变化有多敏感?" 这个敏感度就是梯度 。
方法:链式求导。从损失函数开始,自后向前,层层递推:
1)先计算损失对最后一层参数的偏导数(梯度)。
2)然后利用该结果,计算损失对倒数第二层参数的偏导数。
3)以此类推,一直回溯到第一层。
直观理解:将最终的"误差总分"分解、分摊给网络中每一个应对此错误负责的参数。每一层的梯度计算都依赖于其后一层的梯度结果,形成一个反向的依赖链。 - 更新参数
1)所有参数都获得了自己的梯度(指明了"为使总误差减小,我应朝哪个方向调整")。
2)使用优化器(最基础的是梯度下降 )按以下规则更新所有参数:
新参数 = 旧参数 - 学习率 × 该参数的梯度
学习率:控制每次调整的步长,是一个超参数。
3)物理意义:每个参数都朝着能最快降低总误差的方向,进行一小步调整。