在机器学习分类任务中,仅仅看"准确率(Accuracy)"往往是不够的,尤其是在数据不平衡的情况下。ROC 曲线及其相关指标是评估模型性能、选择判定阈值的核心工具。
什么是 ROC 曲线?
ROC 曲线(Receiver Operating Characteristic Curve),即受试者工作特征曲线。它通过调节分类阈值(Threshold),绘制出:
-
纵轴:真阳性率 (TPR),又称灵敏度 (Sensitivity)。即:真正例中被找出来的比例。
-
横轴:假阳性率 (FPR),即 1 - 特异度 (1 - Specificity)。即:负例中被错误判定为正例的比例。
核心指标:AUC (Area Under Curve)
AUC 代表 ROC 曲线下的面积,取值范围在 0 到 1 之间。
-
AUC = 0.5:代表模型表现等同于随机猜测。
-
AUC > 0.7:代表模型有较好的辨别能力。
-
AUC > 0.9:代表模型表现非常优秀。
关键进阶概念
1. 置信区间 (Confidence Interval, CI)
单单给出一个 AUC 点估计值(如 0.85)是不够稳健的。通过 Bootstrapping(自助法),我们可以计算出 AUC 的 95% 置信区间,从而了解模型性能的波动范围和统计可靠性。
2. 最佳切点 (Optimal Cut-off Point)
模型输出通常是 0 到 1 之间的概率。我们需要一个"切点"来决定超过多少分为阳性。 最常用的方法是 约登指数 (Youden's J statistic):
约登指数最大的点,即为平衡灵敏度和特异度的最佳切点。
单变量诊断效能分析
在很多生信分析或临床研究中,我们并不一定需要构建复杂的神经网络或逻辑回归模型。很多时候,我们手中已经拥有了一个"关键指标 "(例如某个核心基因的表达量、蛋白质浓度、甚至是某种生信算法算出的 Risk Score),我们想知道:仅凭这一个指标,能不能准确区分不同的群体(如肿瘤 vs 正常)?
这种场景下,ROC 曲线依然是评估"判定效能"的黄金标准:
1. 指标即预测值 (Predictor)
在机器学习中,输入是特征,输出是概率;而在"特征-结果"分析中,特征本身就是预测值。
-
例子:如果 CPS1 基因在肿瘤中高表达,在正常组织中低表达,那么 CPS1 的原始表达量数值就可以直接作为横坐标划分的依据。
-
逻辑:ROC 曲线会遍历该指标的所有取值,计算每一个数值作为"切点"时的灵敏度和特异度。
2. 判断指标的"区分力"
通过直接对单个特征进行 ROC 分析,我们可以直观地回答:
-
这个指标够不够敏感?(即使在疾病早期,表达量是否有显著变化)
-
这个指标够不够特异?(是否只在目标疾病中升高,而在对照组中保持稳定)
-
AUC 的直观理解:如果 AUC 为 0.85,意味着如果你随机从肿瘤组抽一个病人,再从正常组抽一个健康人,该指标在肿瘤病人身上数值更高的概率是 85%。
| 维度 | 机器学习预测 | 特征-结果直接关联 |
|---|---|---|
| 输入数据 | 多个特征经过模型融合后的概率值 | 某个具体的基因/蛋白/指标数值 |
| 分析目的 | 验证模型的判别精度 | 寻找具有诊断价值的 Biomarker |
| 最佳切点的意义 | 确定分类概率的阈值 (默认0.5) | 确定具体的生物学浓度或表达量阈值 |
| 核心关注点 | 泛化能力、防止过拟合 | 统计显著性、临床实用性 |
Python 代码实战
下面我们使用 Python 生成模拟数据,绘制 ROC 曲线,并计算 CI 和最佳切点。
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import roc_curve, auc
from sklearn.utils import resample
# 1. 生成模拟数据集
X, y = make_classification(n_samples=1000, n_classes=2, weights=[0.7, 0.3], random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 2. 训练逻辑回归模型并预测概率
model = LogisticRegression()
model.fit(X_train, y_train)
y_probs = model.predict_proba(X_test)[:, 1]
# 3. 计算 ROC 曲线数据
fpr, tpr, thresholds = roc_curve(y_test, y_probs)
roc_auc = auc(fpr, tpr)
# 4. 计算最佳切点 (Youden's J index)
# J = TPR - FPR
j_scores = tpr - fpr
best_idx = np.argmax(j_scores)
best_threshold = thresholds[best_idx]
print(f"最佳切点 (Threshold): {best_threshold:.4f}")
print(f"最佳约登指数 (Youden's J): {j_scores[best_idx]:.4f}")
# 5. 使用 Bootstrapping 计算 AUC 的 95% 置信区间
n_iterations = 1000
bootstrapped_scores = []
for i in range(n_iterations):
# 对测试集进行有放回抽样
indices = resample(np.arange(len(y_test)), replace=True)
if len(np.unique(y_test[indices])) < 2:
continue
score = auc(*roc_curve(y_test[indices], y_probs[indices])[:2])
bootstrapped_scores.append(score)
sorted_scores = np.sort(bootstrapped_scores)
ci_lower = sorted_scores[int(0.025 * len(sorted_scores))]
ci_upper = sorted_scores[int(0.975 * len(sorted_scores))]
print(f"AUC 95% 置信区间: [{ci_lower:.4f} - {ci_upper:.4f}]")
# 6. 绘图
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (AUC = {roc_auc:.3f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
# 绘制最佳切点
plt.scatter(fpr[best_idx], tpr[best_idx], color='red', s=100, marker='o', edgecolors='white', zorder=5, label=f'Best Cut-off ({best_threshold:.2f})')
# 添加箭头指向最佳切点
plt.annotate(f'Best Threshold: {best_threshold:.2f}',
xy=(fpr[best_idx], tpr[best_idx]),
xytext=(fpr[best_idx] + 0.15, tpr[best_idx] - 0.15),
arrowprops=dict(facecolor='black', shrink=0.05, width=2, headwidth=8),
fontsize=12, color='red', fontweight='bold')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate (1 - Specificity)')
plt.ylabel('True Positive Rate (Sensitivity)')
plt.title('Receiver Operating Characteristic (ROC) Analysis')
plt.legend(loc="lower right")
plt.grid(alpha=0.3)
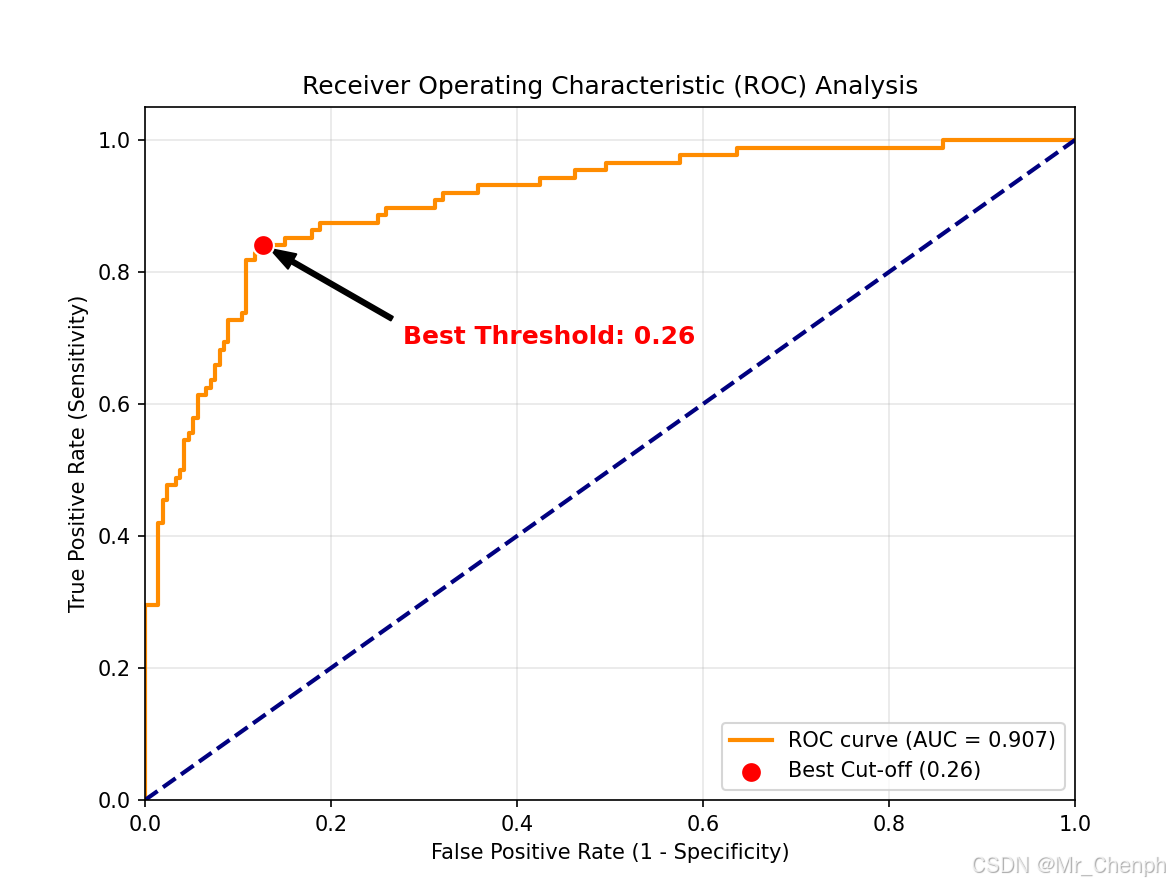
plt.show()结果如下:
- 最佳切点 (Threshold): 0.2609
- 最佳约登指数 (Youden's J): 0.7136
- AUC 95% 置信区间: [0.8654 - 0.9408]