机器学习(5) 梯度下降

目录

• 概念
• 实现
• • 梯度下降直觉
  • 学习率
  • 线性回归的梯度下降
  • 示例

概念

• 假设你有一些代价函数 j ( w , b ) j(w,b) j(w,b)
  J ( w 1 , w 2 , . . . , w n , b ) J(w_1,w_2,...,w_n,b) J(w1,w2,...,wn,b)
• 你想去最小化损失函数，也就是 min ⁡ w 1 , . . . w n , b J ( w 1 , w 2 , . . . w n , b ) \min_{w_1,...w_n,b}J(w_1,w_2,...w_n,b) w1,...wn,bminJ(w1,w2,...wn,b)
• 求解这个的过程就是梯度下降。求解的过程是，给一个起始值 ( w , b ) (w,b) (w,b)，然后不停调整 ( w , b ) (w,b) (w,b)的值，使得让 J ( w , b ) J(w,b) J(w,b)尽可能地小
• 但是对于一些损失函数等高线图非碗形的，这可能有不止一个极值
  
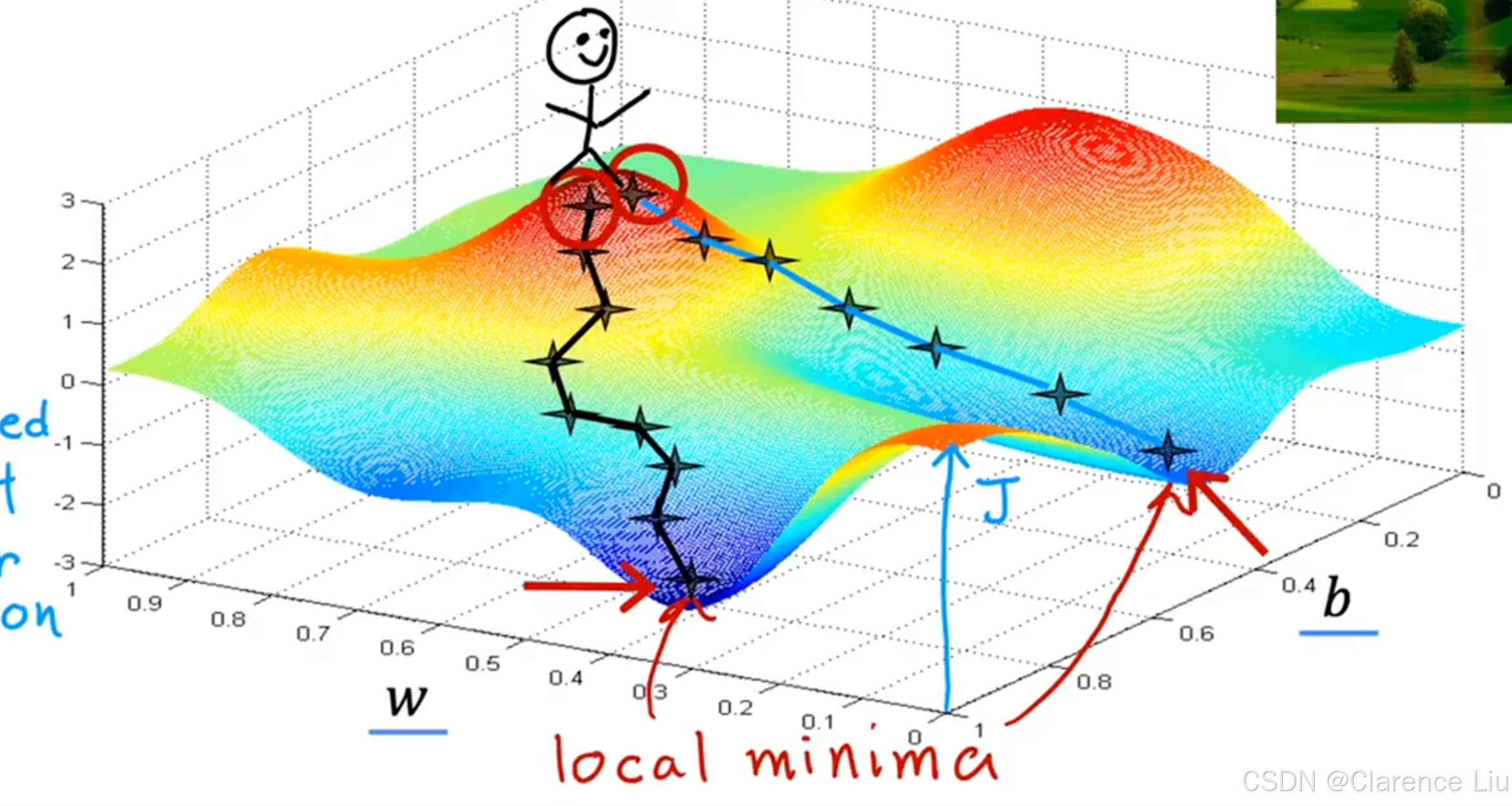
• 像上面这个例子，梯度下降找到的局部最小值有两个

实现

{ w = w − α ∂ ∂ w J ( w , b ) b = b − α ∂ ∂ b J ( w , b ) \begin{cases} w&=w&-&\alpha\frac{\partial}{\partial w}J(w,b)\\ b&=b&-&\alpha\frac{\partial}{\partial b}J(w,b)\\ \end{cases} {wb=w=b−−α∂w∂J(w,b)α∂b∂J(w,b)

• 上面的 α \alpha α被称为学习率 ，通常是一个 ( 0 , 1 ) (0,1) (0,1)之间的数字，作用是控制你更新模型参数 w w w和 b b b的时候，采取的步长。通俗来说就是，下坡的时候步子的大小， α \alpha α非常大，说明下坡的比较大，反之，步子比较小。
• w w w和 b b b要同步更新，并非先更新 w w w再更 b b b

梯度下降直觉

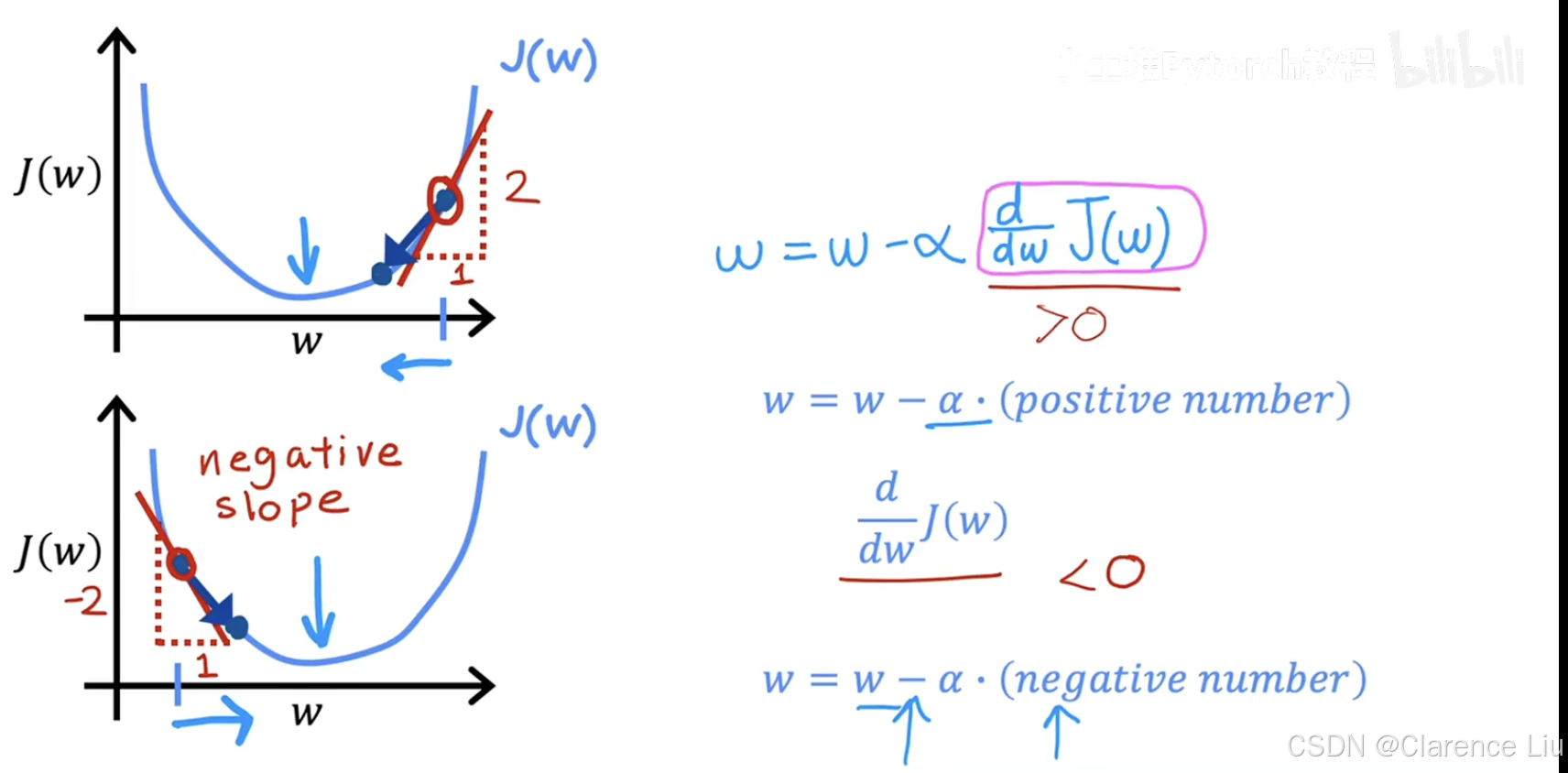
• 下面对一个单参数 w w w的代价函数 J ( w ) J(w) J(w)进行分析，以便于更好的理解梯度下降的正确性。当初始位置位于极小值右侧，因为这点处的切线斜率是一个正数，同时 α \alpha α为正数，所以梯度下降寻找 w w w的过程是一个让 w w w减小的过程；反之，是使得 w w w增大的过程
  

学习率

• 学习率 α \alpha α的选择，对梯度下降实现的效率影响巨大，如果 α \alpha α选择不当，梯度下降可能无法工作。如果 α \alpha α过小，可能需要很多步才能达到极值；如果 α \alpha α过大，可能一步就跳过极值点了，甚至可能无法达到极值点，像下面这个例子
  

线性回归的梯度下降

线性回归模型公式
f w , b ( x ) = w x + b f_{w,b}(x)=wx+b fw,b(x)=wx+b
c o s t f u n c t i o n cost\ function cost function
J ( w , b ) = 1 2 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) 2 J(w,b)=\frac{1}{2m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})^{2} J(w,b)=2m1i=1∑m(fw,b(x(i))−y(i))2

梯度下降
w = w − α ∂ ∂ w J ( w , b ) = w − α × 1 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) x ( i ) w=w-\alpha\frac{\partial}{\partial w}J(w,b)=w-\alpha\times\frac{1}{m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)} w=w−α∂w∂J(w,b)=w−α×m1i=1∑m(fw,b(x(i))−y(i))x(i)
b = b − α ∂ ∂ b J ( w , b ) = α × 1 m ∑ i = 1 m ( f w , b ( x ( i ) ) − y ( i ) ) b=b-\alpha\frac{\partial}{\partial b}J(w,b)=\alpha\times\frac{1}{m}\sum_{i=1}^{m}(f_{w,b}(x^{(i)})-y^{(i)}) b=b−α∂b∂J(w,b)=α×m1i=1∑m(fw,b(x(i))−y(i))

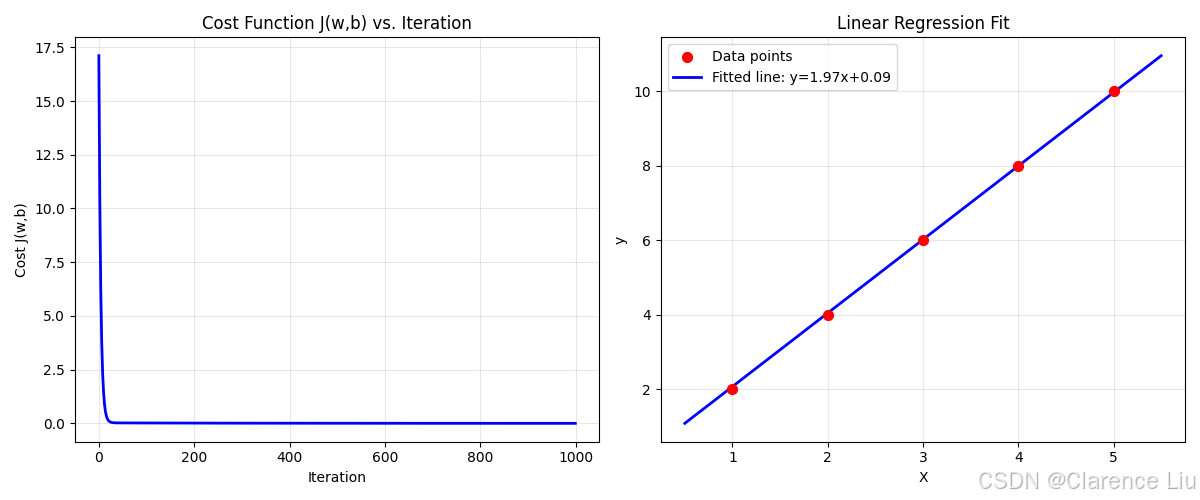
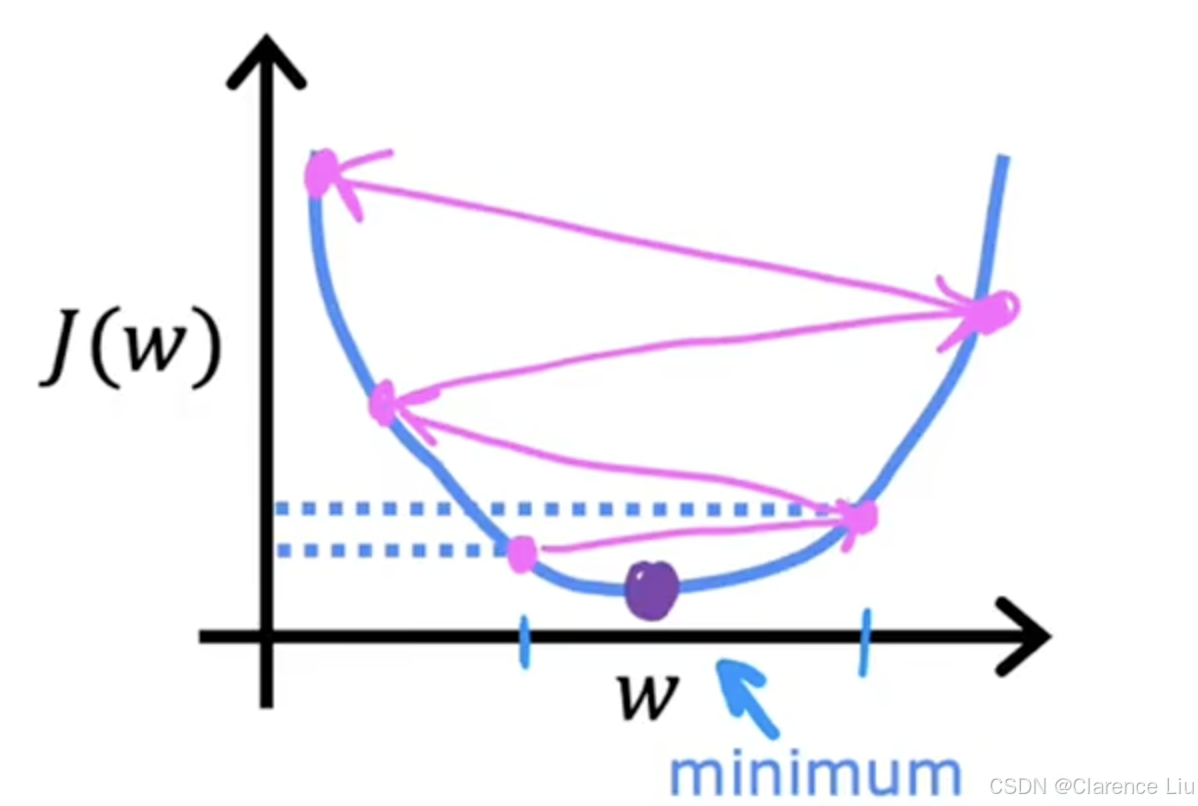
• 对于代价函数是凸函数（两点连线所在区域位于图形上方）的场景，选择合适的学习率总是能够收敛到全局极值点，像下面这个例子

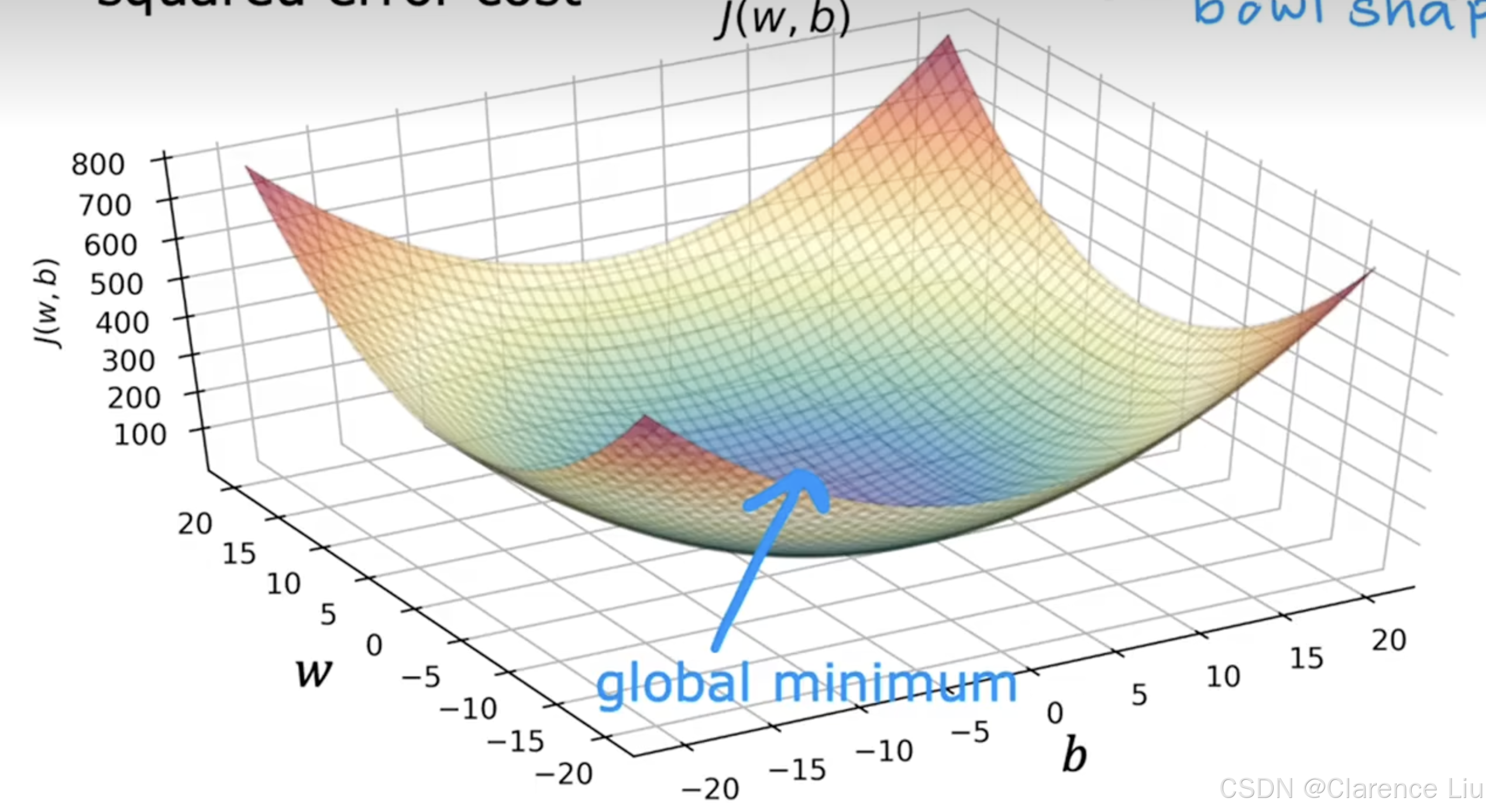
示例

import numpy as np
import matplotlib.pyplot as plt

# f(x) = wx + b
# J(w,b) = (1/2m) * Σ(f(x)-y)²
# w = w - α * (1/m) * Σ(f(x)-y)x
# b = b - α * (1/m) * Σ(f(x)-y)

# 1. 准备数据 - 简单的线性数据
X = np.array([1.0, 2.0, 3.0, 4.0, 5.0])
y = np.array([2.0, 4.0, 6.0, 8.0, 10.0])
m = len(X)

# 2. 公式实现
def compute_cost(X, y, w, b):
    """计算损失函数 J(w,b) = (1/2m) * Σ(f(x)-y)²"""
    total_cost = 0
    for i in range(m):
        f_wb = w * X[i] + b
        cost = (f_wb - y[i]) ** 2
        total_cost += cost
    return total_cost / (2 * m)

def compute_gradient(X, y, w, b):
    """计算梯度
    dj_dw = (1/m) * Σ(f(x)-y)x
    dj_db = (1/m) * Σ(f(x)-y)
    """
    dj_dw = 0
    dj_db = 0
    for i in range(m):
        f_wb = w * X[i] + b
        error = f_wb - y[i]
        dj_dw += error * X[i]
        dj_db += error
    return dj_dw / m, dj_db / m

def gradient_descent(X, y, w_init, b_init, alpha, num_iters):
    """梯度下降算法
    w = w - α * dj_dw
    b = b - α * dj_db
    """
    w = w_init
    b = b_init
    J_history = []
    
    for i in range(num_iters):
        # 计算梯度
        dj_dw, dj_db = compute_gradient(X, y, w, b)
        
        # 同步更新参数
        w = w - alpha * dj_dw
        b = b - alpha * dj_db
        
        # 记录成本
        cost = compute_cost(X, y, w, b)
        J_history.append(cost)
        
        # 每100次迭代输出一次
        if i % 100 == 0:
            print(f"Iteration {i:4d}: Cost {cost:.6f}, w={w:.4f}, b={b:.4f}")
    
    return w, b, J_history

# 3. 运行梯度下降
print("=== 梯度下降示例 ===")
print("数据: X=", X, "y=", y)
print("m =", m)

# 初始化参数
w_init = 0.0
b_init = 0.0
alpha = 0.01  # 学习率
num_iters = 1000

print(f"\n初始参数: w={w_init}, b={b_init}")
print(f"学习率: α={alpha}")
print(f"迭代次数: {num_iters}")

# 执行梯度下降
w_final, b_final, J_history = gradient_descent(X, y, w_init, b_init, alpha, num_iters)

print(f"\n最终参数: w={w_final:.4f}, b={b_final:.4f}")

# 4. 可视化结果
plt.figure(figsize=(12, 5))

# 左侧: 成本函数下降曲线
plt.subplot(1, 2, 1)
plt.plot(J_history, linewidth=2, color='blue')
plt.title('Cost Function J(w,b) vs. Iteration')
plt.xlabel('Iteration')
plt.ylabel('Cost J(w,b)')
plt.grid(True, alpha=0.3)

# 右侧: 数据点和拟合直线
plt.subplot(1, 2, 2)
plt.scatter(X, y, color='red', s=50, label='Data points', zorder=5)
x_line = np.linspace(X.min()-0.5, X.max()+0.5, 100)
y_line = w_final * x_line + b_final
plt.plot(x_line, y_line, color='blue', linewidth=2, label=f'Fitted line: y={w_final:.2f}x+{b_final:.2f}')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression Fit')
plt.legend()
plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 5. 验证结果
print(f"\n=== 结果验证 ===")
print(f"理论最优: w=2.0, b=0.0")
print(f"实际得到: w={w_final:.4f}, b={b_final:.4f}")
print(f"最终成本: {J_history[-1]:.6f}")

# 预测新数据
x_test = 6.0
y_pred = w_final * x_test + b_final
print(f"预测 x={x_test}: y={y_pred:.2f}")