在计算机网络中,数据链路层的主要任务是将网络层交下来的数据报封装成帧,并在两个相邻节点间的链路上进行传输。然而,物理层的传输介质(如铜线、光纤、无线电波)并非理想信道,在传输过程中必然会受到热噪声、脉冲噪声等各种干扰的影响。这些干扰可能导致信号波形发生畸变,从而使接收方判定出的比特流与发送方发送的比特流不一致,例如将 000 误判为 111 或将 111 误判为 000。
这种比特位的改变称为比特差错 。为了保证数据传输的可靠性,数据链路层必须采取措施来检测甚至纠正这些差错,这就是差错控制。
3.4.1 差错控制的基本原理
差错控制的核心思想是冗余(Redundancy) 。发送方在发送数据 DDD 之余,根据某种算法计算出一定的冗余信息 RRR(称为帧检验序列或校验码),并将 DDD 与 RRR 一并发送。接收方收到数据后,利用相同的算法对数据进行检验。
如果我们将所有可能的合法码字集合看作空间中的点,那么差错控制能力的量化指标就是海明距离(Hamming Distance)。
海明距离
两个等长码字之间,对应位不同的位数称为这两个码字的海明距离。例如,码字 101011010110101 和 100111001110011 的海明距离为 222(第3位和第4位不同)。
在一个有效的编码集中,任意两个合法码字之间的最小海明距离 dmind_{min}dmin 决定了该编码系统的检测和纠错能力:
- 检错能力 :若要检测出 ddd 个比特的错误,则编码集的最小海明距离必须满足 dmin≥d+1d_{min} \ge d + 1dmin≥d+1。
- 纠错能力 :若要纠正 ttt 个比特的错误,则编码集的最小海明距离必须满足 dmin≥2t+1d_{min} \ge 2t + 1dmin≥2t+1。
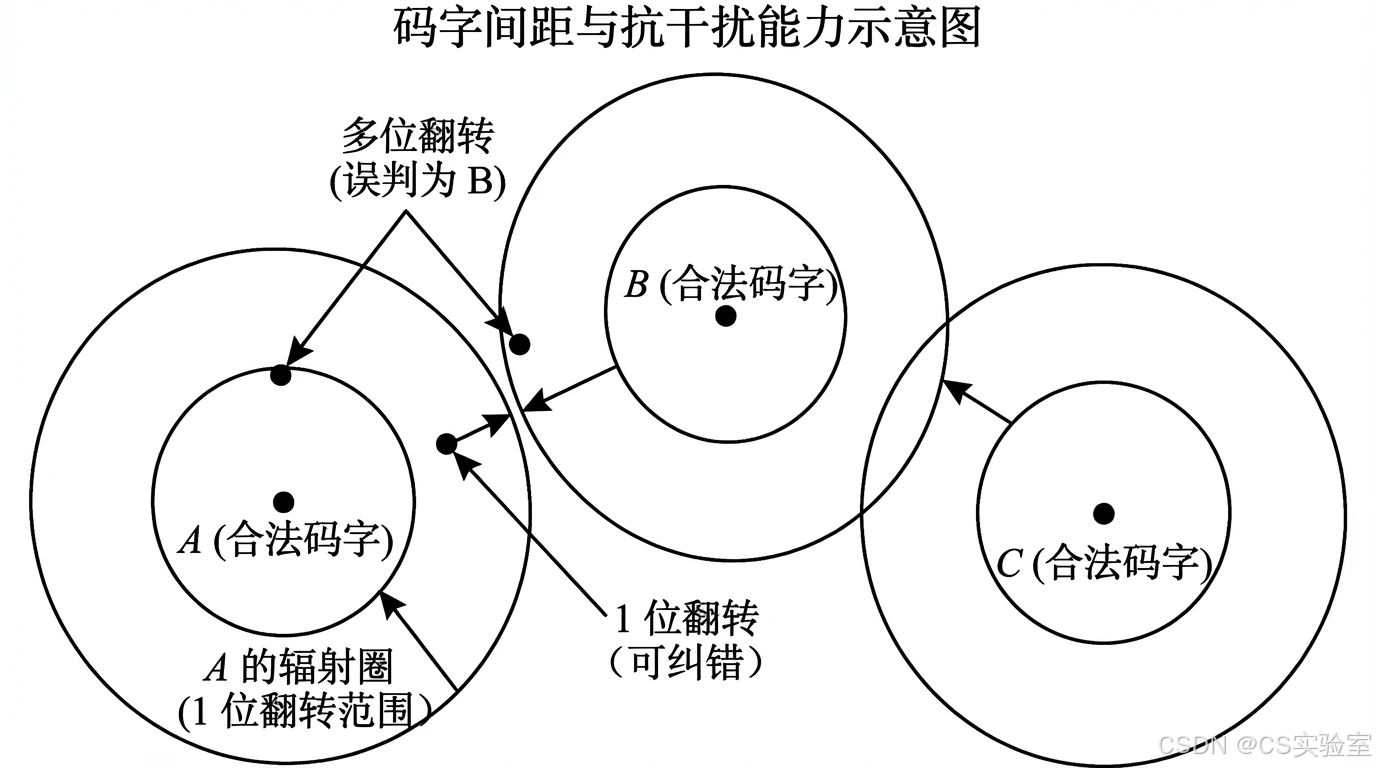
图 3-14 海明距离几何示意图
3.4.2 检错编码 (Error Detection Coding)
检错编码不仅要能够发现错误,而且其计算过程应尽量简单,以减少处理时延。常用的检错编码包括奇偶校验码和循环冗余检验(CRC)。
1. 奇偶校验 (Parity Check)
这是最简单的一种检错方法。它在数据末尾附加一位校验位,使得整个码字(数据位+校验位)中 111 的个数为奇数(奇校验)或偶数(偶校验)。
假设传输的数据为 ASCII 字符 A (010000010100000101000001):
- 奇校验 :原有 111 的个数为 2(偶数),校验位取 111,发送 01000001101000001\mathbf{1}010000011。
- 偶校验 :原有 111 的个数为 2(偶数),校验位取 000,发送 01000001001000001\mathbf{0}010000010。
局限性 :奇偶校验只能检测出奇数个比特的错误。如果传输中同时有 2 个比特发生翻转(例如 0→10 \to 10→1 且 1→01 \to 01→0),校验结果依然"正确",导致漏检。因此,它通常仅用于低速或对可靠性要求不高的环境。
2. 循环冗余检验 (Cyclic Redundancy Check, CRC)
CRC 是目前数据链路层应用最广泛的检错技术,广泛应用于以太网、Wi-Fi 等协议中。它利用了多项式除法的数学原理。
基本原理:
- 多项式表示 :将一个 kkk 位的比特串看作一个 k−1k-1k−1 阶的多项式。例如 110111011101 对应多项式 M(x)=1⋅x3+1⋅x2+0⋅x1+1⋅x0=x3+x2+1M(x) = 1 \cdot x^3 + 1 \cdot x^2 + 0 \cdot x^1 + 1 \cdot x^0 = x^3 + x^2 + 1M(x)=1⋅x3+1⋅x2+0⋅x1+1⋅x0=x3+x2+1。
- 生成多项式 G(x)G(x)G(x) :收发双方预先约定一个 rrr 阶的生成多项式 G(x)G(x)G(x)(其最高位和最低位必须为 1)。
- 计算过程 :
- 设待发送数据为 MMM,共 kkk 位。
- 在 MMM 后面添加 rrr 个 000,得到 2rM2^r M2rM。
- 使用模2除法 (即异或运算,不借位减法),计算 2rM2^r M2rM 除以 G(x)G(x)G(x) 的余数。
- 得到的 rrr 位余数即为帧检验序列 (FCS)。
- 最终发送的数据为:MMM 级联 FCSFCSFCS。
模2运算规则 :
0⊕0=0,1⊕1=0,0⊕1=1,1⊕0=1 0 \oplus 0 = 0, \quad 1 \oplus 1 = 0, \quad 0 \oplus 1 = 1, \quad 1 \oplus 0 = 1 0⊕0=0,1⊕1=0,0⊕1=1,1⊕0=1
示例 :
假设待发送数据 M=101001M = 101001M=101001,约定生成多项式 G(x)=1101G(x) = 1101G(x)=1101(即阶数 r=3r=3r=3)。
- 补零 :MMM 后补 3 个 0,被除数为 101001000101001000101001000。
- 除法运算:
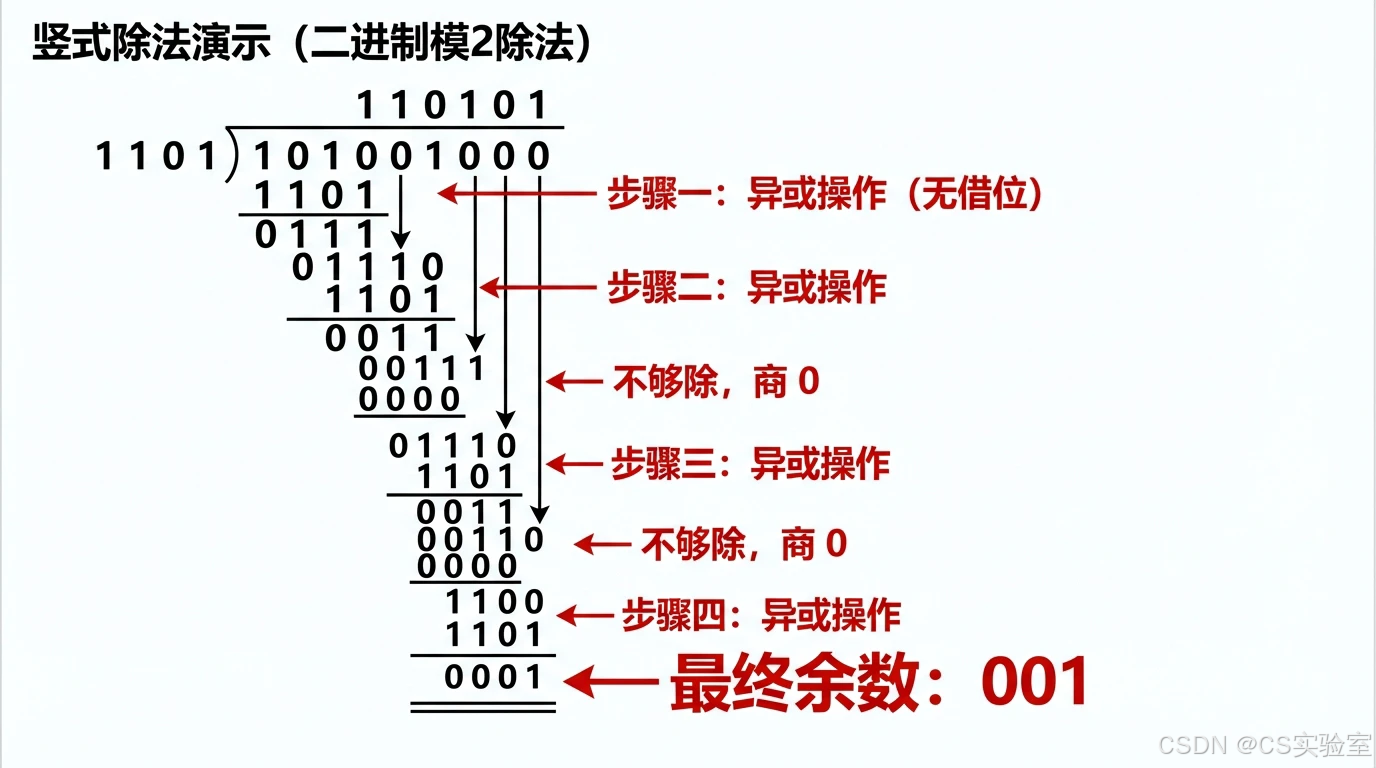
图 3-15 CRC模2除法运算过程
- 结果 :余数为 001001001。最终发送数据为 101001001101001\mathbf{001}101001001。
接收方收到数据后,用同样的生成多项式 G(x)G(x)G(x) 进行模2除法。若余数为 000,则认为传输无差错;否则丢弃该帧。
CRC的优势 :CRC 能够检测出所有的单比特错误、双比特错误、奇数个错误以及长度小于等于 rrr 的突发错误(Burst Error)。由于其易于通过硬件(移位寄存器)实现,处理速度极快。
3.4.3 纠错编码 (Error Correction Coding)
在某些信道质量极差(如无线链路)或传输延迟极高(如卫星通信)的场景下,发现错误后要求对方重传的代价太大。此时,需要使用前向纠错(Forward Error Correction, FEC),即不仅能发现错误,还能定位并纠正错误。
海明码 (Hamming Code)
海明码是最著名的纠错码之一,能够纠正一位比特错误。
校验位的位置与数量 :
设数据位为 mmm 位,校验位为 rrr 位,总长度 n=m+rn = m + rn=m+r。为了能指示出 nnn 位中哪一位出错(或者无错),校验位的状态数 2r2^r2r 必须覆盖所有可能情况:
2r≥m+r+1 2^r \ge m + r + 1 2r≥m+r+1
校验位通常放置在 222 的幂次位置(第 1, 2, 4, 8... 位)。
编码规则 :
每个校验位 PiP_iPi 负责校验部分数据位。其规则是:若某数据位的二进制位置索引中,第 iii 位为 1,则该数据位由 PiP_iPi 负责。
例如,对于 8 位数据(实际上常用的是 4 数据位 + 3 校验位的海明(7,4)码):
- P1P_1P1 (第1位, 0012001_20012) 负责位置:1, 3, 5, 7, 9...
- P2P_2P2 (第2位, 0102010_20102) 负责位置:2, 3, 6, 7, 10...
- P4P_4P4 (第4位, 1002100_21002) 负责位置:4, 5, 6, 7, 12...
发送方计算各校验位的值(通常采用偶校验)。接收方重新计算这些校验关系,得到 rrr 位的指错字(Syndrome)。若指错字为 000000000,则无错;若为 011011011(十进制 3),则说明第 3 位发生了错误,将其取反即可纠正。
3.4.4 应用场景与发展
在实际的计算机网络中,差错控制策略的选择取决于链路特性。
-
有线网络(如光纤、双绞线):
- 特点 :误码率极低(通常低于 10−910^{-9}10−9)。
- 策略 :主要采用检错编码(CRC)配合反馈重传(ARQ)。如果发现错误,直接丢弃帧,依靠上层(如 TCP)或数据链路层的确认机制要求重传。因为出错概率极低,纠错带来的额外冗余开销是不划算的。
-
无线网络(如 Wi-Fi, 5G, 卫星通信):
- 特点:干扰大,信号衰减快,误码率高。
- 策略 :必须采用纠错编码(FEC)。
- 现代发展 :现代无线通信早已超越了简单的海明码,广泛采用了更高效的编码技术:
- Turbo 码:用于 3G/4G 通信,性能逼近香农极限。
- LDPC 码 (低密度奇偶校验码):Wi-Fi 6 和 5G 数据信道的标准编码,具有极高的并行解码效率和纠错能力。
- Polar 码 (极化码):华为推崇的技术,被用于 5G 控制信道,是目前唯一理论上证明可以达到香农极限的编码方案。
本节小结
- 差错性质:差错控制分为检错和纠错。
- 核心指标:海明距离决定了编码系统的检错和纠错能力。
- 主流技术:CRC 是检错的工业标准,广泛用于以太网;海明码是纠错的基础;LDPC 等现代编码支撑了高速无线通信。
- 设计权衡:在低误码率链路使用"检错+重传"以提高效率;在高误码率或高延迟链路使用"前向纠错"以保证可靠性。