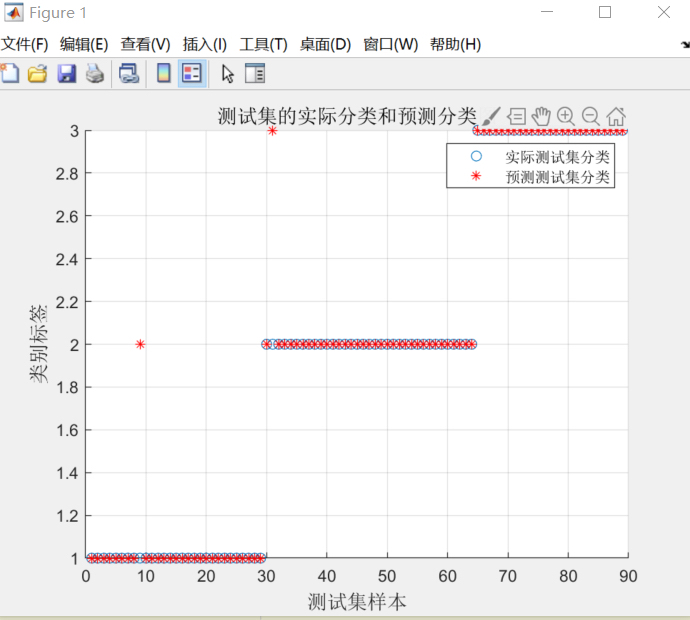
使用粒子群算法PSO优化最小支持向量机LSSVM实现分类

使用粒子群算法PSO优化最小支持向量机LSSVM实现分类，其中PSO通过优化LSSVM模型中的c和g的参数，利用PSO算法寻优得到最优的bestc和bestg变量，然后赋值到LSSVM模型中，进而实现提升LSSVM的建模效果

最近在研究分类算法，发现了一种很有意思的组合：用粒子群算法（PSO）来优化最小支持向量机（LSSVM）。今天就来和大家分享一下这个过程😃

粒子群算法PSO简介

粒子群算法是一种基于群体智能的优化算法。它模拟鸟群觅食等群体行为，通过粒子在解空间中的飞行和更新来寻找最优解。

想象一下，一群粒子在一个空间里飞，每个粒子都有自己的位置和速度。它们一边飞一边根据自己当前的位置和群体中最优粒子的位置来调整自己的飞行方向和速度。

python 复制代码

import numpy as np

# 初始化粒子群
def initialize_particles(num_particles, dim):
    particles = np.random.uniform(-1, 1, size=(num_particles, dim))
    velocities = np.zeros((num_particles, dim))
    return particles, velocities

在这段代码里，initialize_particles函数用来初始化粒子群。我们随机生成粒子的初始位置，范围在[-1, 1]之间，速度初始化为0。

最小支持向量机LSSVM

最小支持向量机是支持向量机的一种改进形式，它通过求解线性方程组来得到分类超平面，计算量相对较小。

LSSVM的核心在于求解下面这个优化问题：

\begin{align*}

\min*{\mathbf{w},b,\xi} &\frac{1}{2}\mathbf{w}^T\mathbf{w} + \frac{C}{2}\sum*{i=1}^{n}\xi_i^2 \\

\text{s.t.} &\ y*i(\mathbf{w}^T\mathbf{x}*i + b) \geq 1 - \xi_i, \quad i = 1,\cdots,n \\

& \xi_i \geq 0, \quad i = 1,\cdots,n

\end{align*}

其中，\(\mathbf{w}\)是权重向量，\(b\)是偏置，\(\xi_i\)是松弛变量，\(C\)是惩罚因子。

PSO优化LSSVM

我们要用PSO来优化LSSVM中的参数。这里主要优化两个参数：惩罚因子\(C\)（在代码里用c表示）和核函数参数\(g\)（在代码里用g表示）。

python 复制代码

# 定义适应度函数，这里用分类准确率作为适应度
def fitness_function(particles, X, y):
    accuracies = []
    for particle in particles:
        c = particle[0]
        g = particle[1]
        model = LSSVM(c, g)
        model.fit(X, y)
        y_pred = model.predict(X)
        accuracy = np.mean(y_pred == y)
        accuracies.append(accuracy)
    return accuracies

fitness_function函数计算每个粒子对应的LSSVM模型在数据集上的分类准确率，以此作为适应度值。

然后在PSO的迭代过程中，不断更新粒子的位置和速度：

python 复制代码

# PSO迭代更新
def pso_update(particles, velocities, fitness_values, best_particles, best_fitness, w, c1, c2, dim):
    r1 = np.random.rand(particles.shape[0], dim)
    r2 = np.random.rand(particles.shape[0], dim)
    velocities = w * velocities + c1 * r1 * (best_particles - particles) + c2 * r2 * (np.tile(best_particles, (particles.shape[0], 1)) - particles)
    particles = particles + velocities
    new_fitness = fitness_function(particles, X, y)
    for i in range(particles.shape[0]):
        if new_fitness[i] > best_fitness[i]:
            best_particles[i] = particles[i]
            best_fitness[i] = new_fitness[i]
    return particles, velocities, best_particles, best_fitness

在这个更新函数里，通过计算新的位置和速度，比较新的适应度值和历史最优适应度值，更新全局最优粒子和最优适应度。

经过多次迭代后，PSO会找到最优的c和g值：

python 复制代码

# 运行PSO
num_particles = 30
dim = 2
w = 0.7
c1 = 1.5
c2 = 1.5
max_iter = 50

particles, velocities = initialize_particles(num_particles, dim)
best_particles = particles.copy()
best_fitness = fitness_function(particles, X, y)

for _ in range(max_iter):
    particles, velocities, best_particles, best_fitness = pso_update(particles, velocities, best_fitness, best_particles, best_fitness, w, c1, c2, dim)

bestc = best_particles[np.argmax(best_fitness)][0]
bestg = best_particles[np.argmax(best_fitness)][1]

最后得到最优的bestc和bestg，把它们赋值到LSSVM模型中，就可以提升LSSVM的建模效果啦😎

通过这样的方式，利用粒子群算法的寻优能力，我们有效地优化了最小支持向量机的参数，从而在分类任务中可能获得更好的性能。大家如果有兴趣也可以试试，看看在自己的数据上效果怎么样🧐

以上代码只是一个简单的示例，实际应用中可能还需要根据具体情况进行更多的调整和优化哦。

希望这篇分享对大家理解和应用PSO优化LSSVM有所帮助😃

#PSO #LSSVM #分类算法 #优化