题目内容

题目原始内容参考
https://www.ninedata.cloud/sql_sudo2025
sudoku 9_9 ( 进阶挑战 )
数据规模: 1 万 rows
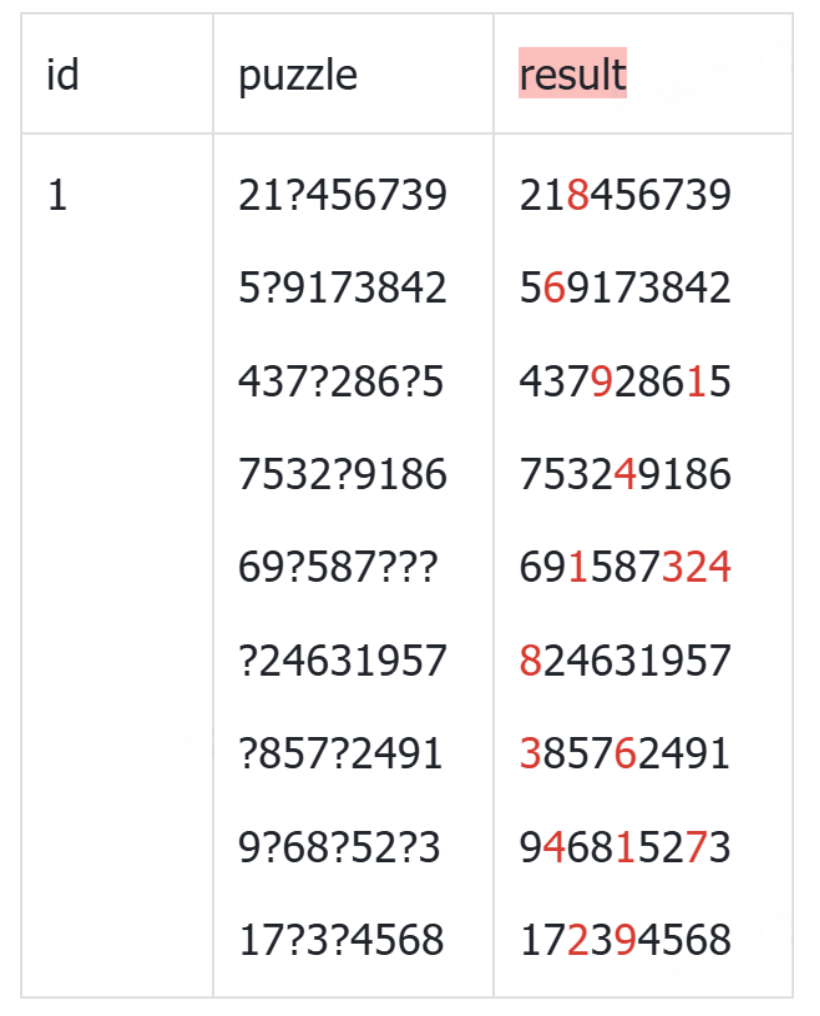
使用一条 SQL 给出如下图的结果。字段 id 为自增字段的数字主键,字段 puzzle 是题目内容,由 9×9 个数字组成,问号表示未知的数字。其中 result 字段是选手需要给出数独的解。
数独求解规则
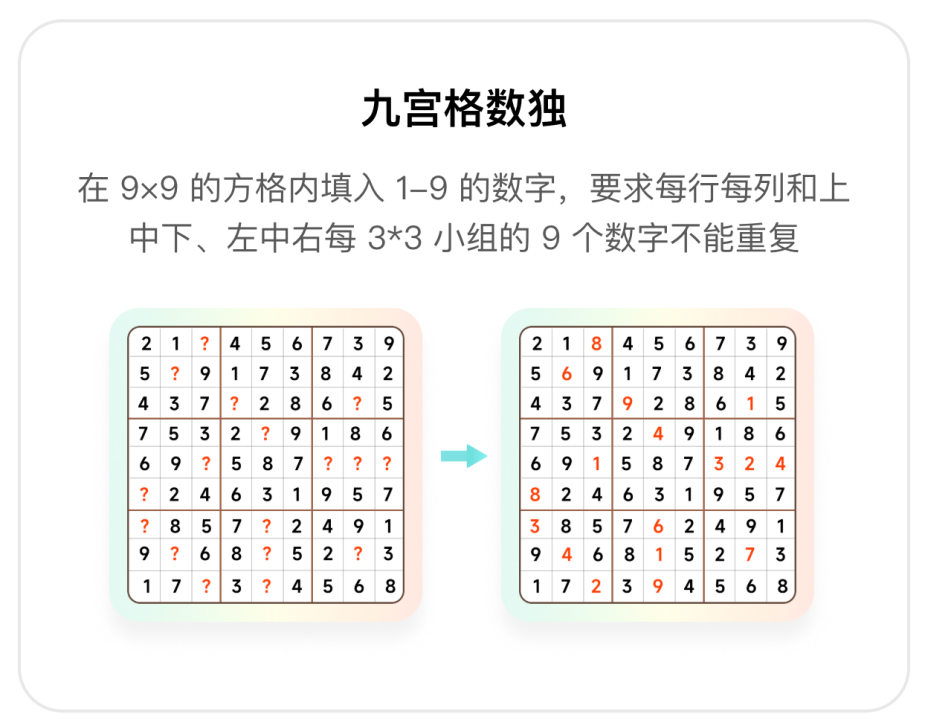
四宫格数独(普通挑战):在 4x4 的方格内填入数字 1-4 ,要求每每行每列和每组的数字不能重复。
九宫格数独(进阶挑战):在 9x9 的方格内填入数字 1-9 ,要求每行每列和每组的数字不能重复。
完成普通挑战的选手,可以进一步完成进阶挑战。进阶挑战性能得分加解题正确性得分排名前8的选手进入决赛成绩评选。
进入决赛要求解题正确率大于80%
(注:提交进阶挑战 SQL 前必须先提交普通挑战的 SQL )
SQL 要求
仅允许使用一条 SQL 语句,允许使用数据库内置函数,不允许使用存储过程/自定义函数和代码块。
SQL 执行时间不超过 5 分钟,超过 5 分钟则认为成绩无效。
提交的 SQL 不能超过 10 KB 大小
解题思路
代码测试环境:oracle11g
说明:所用的sql代码都是oracle标准功能,oracle19c兼容。
赛题示例中的 " ?",就是待填入数字的位置,为了方便说明算法,后面统一按照单元格这种名称进行描述。
看到数独这个比赛题目,首先想到的就是曾经自己的玩法。
9x9的数独,就是有81个单元格,空白单元格看成未知数,那么就是根据该单元格所在的行、列、区域的已有值,排除掉数字1-9中的八个,剩下的那个就是要填入空白单元格的值。
按照以上算法思路,首先将字符串拆解成单元格形式:加入行号、列号、区域号,按照行列区域定位每个单元格。
拆解完成后,使用oracle的model子句,实现算法描述的:根据该单元格所在的行、列、区域的已有值,排除掉数字1-9中的八个,剩下的那个就是要填入空白单元格的值。
oracle的model子句可以以类似excel表格形式进行单元格的计算,并且下次计算可以直接使用上次计算结果。要注意的是,这个思路的代码如果遇到一个单元格有两个或以上可能值,始终无法排除掉,那么就无法解出数独。
解题代码
with q as (
select
id,puzzle
from sudoku9_9)
,q2 as (
-- 构造行列区域编号,用于定位1-9的分布
select
id,puzzle,i,rowno,colno
,case when rowno in (1,2,3) and colno in (1,2,3) then 1
when rowno in (1,2,3) and colno in (4,5,6) then 2
when rowno in (1,2,3) and colno in (7,8,9) then 3
when rowno in (4,5,6) and colno in (1,2,3) then 4
when rowno in (4,5,6) and colno in (4,5,6) then 5
when rowno in (4,5,6) and colno in (7,8,9) then 6
when rowno in (7,8,9) and colno in (1,2,3) then 7
when rowno in (7,8,9) and colno in (4,5,6) then 8
when rowno in (7,8,9) and colno in (7,8,9) then 9
end areno
,to_number(case when substr(puzzle,i,1)='?' then '0' else substr(puzzle,i,1) end) c1
from (
select
id,puzzle,i
,case when i<=10 then 1
when i<=20 then 2
when i<=30 then 3
when i<=40 then 4
when i<=50 then 5
when i<=60 then 6
when i<=70 then 7
when i<=80 then 8
when i<=90 then 9
end rowno
,mod(i,10) colno
from (
-- 构造行用于拆分数独
select level i
from dual
connect by level <=89
) qr,q
)qrc where colno!=0
)
,q3 as(
-- 数独运算过程
select id,puzzle,rowno,colno,areno,c1,c1n,c2n
from q2 -- where id=2
model
partition by (id,puzzle)
dimension by (rowno,colno,areno)
measures (c1, 0 c1n, 0 c2n)
rules iterate(9)(
-- 1 标记单元格不可能的值 行、列、区域
c1n[any,any,any] = case when c1[cv(),cv(),cv()]=0 then listagg(case when c1=0 then to_number('') else c1 end) within group (order by colno) over (partition by id,rowno)
|| listagg(case when c1=0 then to_number('') else c1 end) within group (order by rowno) over (partition by id,colno)
|| listagg(case when c1=0 then to_number('') else c1 end) within group (order by rowno,colno) over (partition by id,areno)
else to_number('') end
-- 构建非重复序列
,c2n[any,any,any]=case when instr(c1n[cv(),cv(),cv()],'1')>0 then '1' end
||case when instr(c1n[cv(),cv(),cv()],'2')>0 then '2' end
||case when instr(c1n[cv(),cv(),cv()],'3')>0 then '3' end
||case when instr(c1n[cv(),cv(),cv()],'4')>0 then '4' end
||case when instr(c1n[cv(),cv(),cv()],'5')>0 then '5' end
||case when instr(c1n[cv(),cv(),cv()],'6')>0 then '6' end
||case when instr(c1n[cv(),cv(),cv()],'7')>0 then '7' end
||case when instr(c1n[cv(),cv(),cv()],'8')>0 then '8' end
||case when instr(c1n[cv(),cv(),cv()],'9')>0 then '9' end
-- 1 对排除八个可能值的无值单元格 赋值
,c1[any,any,any]=case when c1[cv(),cv(),cv()]=0 and length(c2n[cv(),cv(),cv()])=8 then
45-substr(c2n[cv(),cv(),cv()],1,1)-substr(c2n[cv(),cv(),cv()],2,1)-substr(c2n[cv(),cv(),cv()],3,1)
-substr(c2n[cv(),cv(),cv()],4,1)-substr(c2n[cv(),cv(),cv()],5,1)-substr(c2n[cv(),cv(),cv()],6,1)
-substr(c2n[cv(),cv(),cv()],7,1)-substr(c2n[cv(),cv(),cv()],8,1)
else c1[cv(),cv(),cv()] end
))
-- 输出数独结果
select id,puzzle
,listagg(case when colno=9 then c1||chr(10) else c1||'' end) within group (order by rowno,colno) result
from q3
group by id,puzzle