前言
STL 中 stack 与 queue 本质是容器适配器,基于基础容器封装实现特定操作逻辑。本文先介绍容器适配器及二者核心概念,再手动模拟实现,最后通过几道算法题展示其应用,助力夯实 STL 设计思想与数据结构基础。
☃ C++ 初阶
【......】
目录
---------------stack---------------
[问题:为啥 stack 不用提供默认成员函数?](#问题:为啥 stack 不用提供默认成员函数?)
---------------queue--------------
--------------算法题--------------
------------容器适配器------------
1、什么是容器适配器?
适配器可以理解为 "转换器"------ 它能把原本不兼容、不符合需求的对象(比如函数、容器等),改造为可以直接使用、适配特定场景的形式。
容器适配器是适配器的一种,它专门用来包装底层容器(例如 deque、vector):通过屏蔽底层容器的复杂接口,只暴露栈、队列等特定数据结构的核心操作(比如 stack 的 push/pop,queue 的 front/back),让我们可以直接按照经典数据结构的逻辑来使用它。
2、为啥容器配置器不支持迭代器
stack:仅允许操作栈顶(遵循后进先出 LIFO 规则),若暴露迭代器,用户就能遍历栈内所有元素,这会破坏它的设计意图。
queue:仅允许操作队首 / 队尾(遵循先进先出 FIFO 规则),迭代器会打破 "队列只能从两端操作" 的限制。
priority_queue:仅允许操作优先级最高的元素(堆顶),遍历其底层存储(比如用 vector 实现的堆)没有实际意义 ------ 底层存储的顺序并非优先级顺序。
容器适配器的价值,正是用极简的接口解决特定场景的问题(比如栈只需要 push/pop/top)。而迭代器是 "通用遍历" 的工具,和适配器 "限制访问" 的核心目标完全相悖,因此二者天生不兼容。
在 C++ STL 中,容器适配器只有上述 3 种,本文我们只讲解前两种。
---------------stack---------------
1、stack介绍
stack 的定位:stack 是一种容器适配器,专门用于 "后进先出(LIFO)" 的场景,元素的插入和提取操作只能在容器的一端进行。
stack 的实现逻辑:作为容器适配器,stack 是通过包装某一底层容器实现的 ------ 它会以该容器为基础,提供一组特定的成员函数来访问元素;其中,底层容器的尾部会被当作栈顶,元素的压入、弹出操作都在这一端完成。
stack 对底层容器的要求:stack 的底层容器可以是任意标准容器模板,或是满足以下操作的特定容器:
**
empty:**判断容器是否为空**
back:**获取容器尾部的元素**
push_back:**在容器尾部插入元素**
pop_back:**删除容器尾部的元素
默认底层容器:标准容器vector、deque、list都满足上述要求;若未显式指定 stack 的底层容器,默认会使用deque。
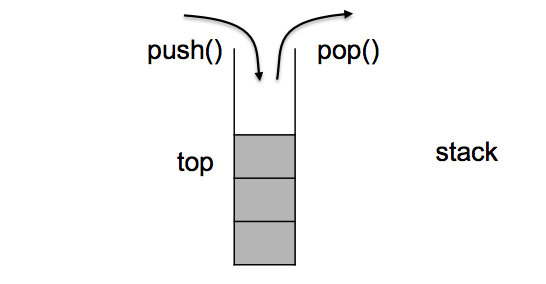
2、stack模拟实现
cpp
namespace bit
{
// 容器适配器:模拟实现stack(LIFO 后进先出)
// T:元素类型;Container:底层存储容器,默认deque<T>
template<class T, class Container = deque<T>>
class stack
{
public:
// 压栈:将x插入栈顶
void push(const T& x)
{
_con.push_back(x);
}
// 出栈:删除栈顶元素(不返回值)
void pop()
{
_con.pop_back();
}
// 获取栈顶元素(const引用返回,避免拷贝)
const T& top()
{
return _con.back();
}
// 判断栈是否为空
bool empty()
{
return _con.empty();
}
// 获取栈中元素个数
size_t size()
{
return _con.size();
}
private:
Container _con; // 底层容器,实际存储数据
};
}deque是双端队列,虽名字带 "队列",但和 FIFO 结构的队列无实际关联。它是支持头尾高效增删、可随机访问的双端动态容器,是 STL 中灵活高效的基础容器之一。下一章会简单介绍它,目前大家可以先把它当作类似 vector 和 list 的容器来理解。
Container _con:是stack的底层容器对象 ,实际存储所有元素;stack的所有操作都是通过封装这个容器的接口实现的(体现 "适配器" 的封装思想)。
☃. 接口介绍:
**push(const T& x):**调用底层容器_con的push_back,把元素x插入到栈顶(对应容器尾部)。
**pop():**调用_con的pop_back,删除栈顶元素(不返回值)。
**const T& top():**返回_con.back(),即栈顶元素的const引用(避免拷贝,也防止外部修改)。
**empty():**返回_con.empty()的结果,判断栈是否为空。
**size():**返回_con.size(),获取栈中元素的个数。
问题:为啥 stack 不用提供默认成员函数?
回答 :因为编译器会自动为stack生成默认成员函数(包括默认构造、拷贝构造、赋值重载、析构函数等),而这些自动生成的函数会调用底层容器(如deque)的对应函数 ------ 比如默认构造调用容器的无参构造、拷贝构造调用容器的拷贝构造,能完整实现stack的初始化、拷贝、资源释放等需求。同时stack是容器适配器,自身不管理额外动态资源,所有功能都依赖底层容器,因此无需手动提供默认成员函数。
---------------queue--------------
1、queue介绍
queue 的定位:队列是一种容器适配器,专门用于在 FIFO(先进先出)上下文中操作,其中从容器一端插入元素,另一端提取元素。
queue 的实现逻辑:队列作为容器适配器实现,容器适配器即将特定容器类封装作为其底层容器类,queue 提供一组特定的成员函数来访问其元素。元素从队尾入队列,从队头出队列。
queue 对底层容器的要求:底层容器可以是标准容器类模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:
**empty:**检测队列是否为空
**size:**返回队列中有效元素的个数
**front:**返回队头元素的引用
**back:**返回队尾元素的引用
**push_back:**在队列尾部入队列
**pop_front:**在队列头部出队列
queue 的默认底层容器:标准容器类 deque 和 list 满足了这些要求。默认情况下,如果没有为 queue 实例化指定容器类,则使用标准容器 deque。
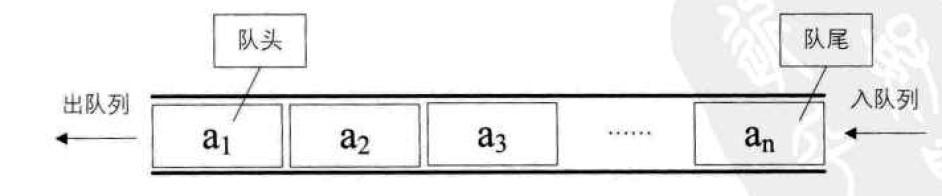
2、queue模拟实现
cpp
namespace bit
{
// 容器适配器:模拟实现queue(FIFO 先进先出)
// T:元素类型;Container:底层存储容器,默认用deque<T>
template<class T, class Container = deque<T>>
class queue
{
public:
// 入队:将元素x插入队列尾部(复用底层容器的尾插)
void push(const T& x)
{
_con.push_back(x);
}
// 出队:删除队列头部元素(复用底层容器的头删)
void pop()
{
_con.pop_front();
}
// 获取队列头部元素(const引用返回,避免拷贝、防止外部修改)
const T& front()
{
return _con.front();
}
// 获取队列尾部元素(const引用返回,避免拷贝、防止外部修改)
const T& back()
{
return _con.back();
}
// 判断队列是否为空(复用底层容器的判空)
bool empty()
{
return _con.empty();
}
// 获取队列中元素的个数(复用底层容器的size)
size_t size()
{
return _con.size();
}
private:
Container _con; // 底层容器,实际存储队列的所有元素
};
}**Container _con:**是 queue 的底层容器对象,实际存储所有元素;queue 的所有操作都是通过封装这个容器的接口实现的(体现 "适配器" 的封装思想)。
☃. 接口介绍:
**push (const T& x):**调用底层容器_con 的 push_back,把元素 x 插入到队列尾部(对应容器尾部)。
**pop ():**调用_con 的 pop_front,删除队列头部元素(不返回值)。
**const T& front ():**返回_con.front (),即队列头部元素的 const 引用(避免拷贝,也防止外部修改)。
**const T& back ():**返回_con.back (),即队列尾部元素的 const 引用(避免拷贝,也防止外部修改)。
**empty ():**返回_con.empty () 的结果,判断队列是否为空。
**size ():**返回_con.size (),获取队列中元素的个数。
--------------算法题--------------
1、最小栈
【题目链接】: https://leetcode.cn/problems/min-stack/description/

【思路分析】
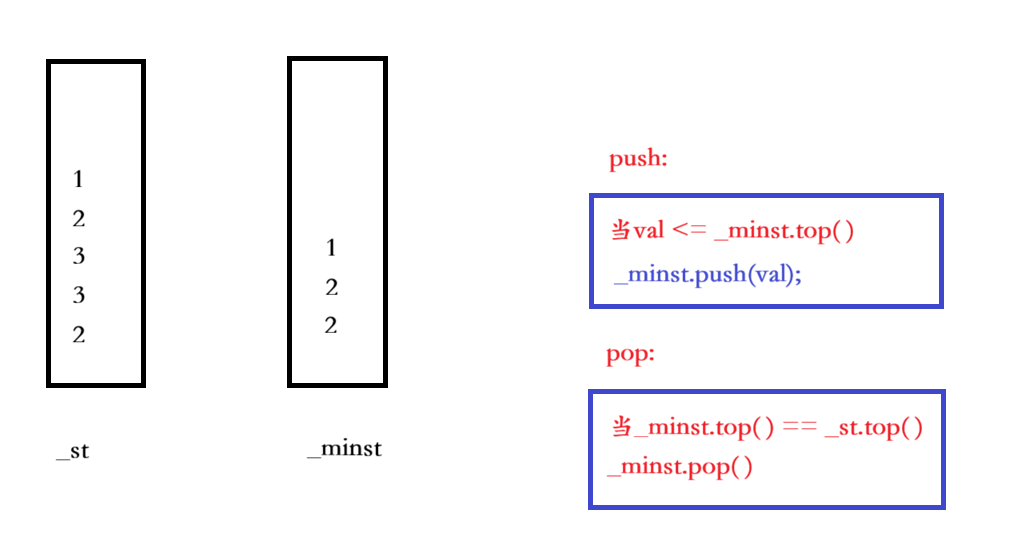
用一个数据栈存储所有入栈元素,另一个最小值栈同步维护对应阶段的栈内最小值;入栈时仅当新元素小于等于最小值栈顶(或最小值栈为空)时,才将其压入最小值栈;出栈时若弹出的元素是当前最小值(与最小值栈顶相等),则同步弹出最小值栈顶;获取最小值直接返回最小值栈顶,实现 O (1) 时间复杂度的查询,同时保证入栈、出栈操作高效可行。
【示例代码】
cpp
class MinStack {
public:
MinStack() {
}
void push(int val) {
_st.push(val); // 压入数据栈
// 维护最小值栈,空或当前值≤栈顶时压入
if(_minst.empty() || val <= _minst.top())
{
_minst.push(val);
}
}
void pop() {
// 弹出的是最小值时,同步弹出最小值栈
if(_minst.top() == _st.top())
{
_minst.pop();
}
_st.pop(); // 弹出数据栈
}
int top() {
return _st.top(); // 返回数据栈顶
}
int getMin() {
return _minst.top(); // 返回最小值栈顶
}
private:
stack<int> _st; // 数据栈:存储所有元素
stack<int> _minst; // 最小值栈:存储各阶段最小值
};2、栈的压入、弹出序列
【题目链接】: https://www.nowcoder.com/practice/d77d11405cc7470d82554cb392585106
【思路分析】
模拟栈的入栈、出栈过程,最终栈为空则代表符合规则:
先将元素入栈,若当前入栈元素与出栈数组的待匹配元素一致,则让该入栈元素出栈,同时出栈数组的匹配指针后移;重复这一过程,直到所有元素处理完后,若栈为空,说明入栈、出栈的顺序是合法的。
【示例代码】
cpp
class Solution {
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
stack<int> st;//模拟出入栈
int pushi = 0;
int popi = 0;
//入完了就跳出循环
while(pushi < pushV.size())
{
st.push(pushV[pushi++]);
//不匹配
if(st.top() != popV[popi])
{
continue;
}//匹配
else {
while(!st.empty() && st.top() == popV[popi])
{
popi++;
st.pop();
}
}
}
//等于空说明符合栈的规则
return st.empty();
}
};3、逆波兰表达式求值
【题目链接】: https://leetcode.cn/problems/evaluate-reverse-polish-notation/description/

【思路解析】
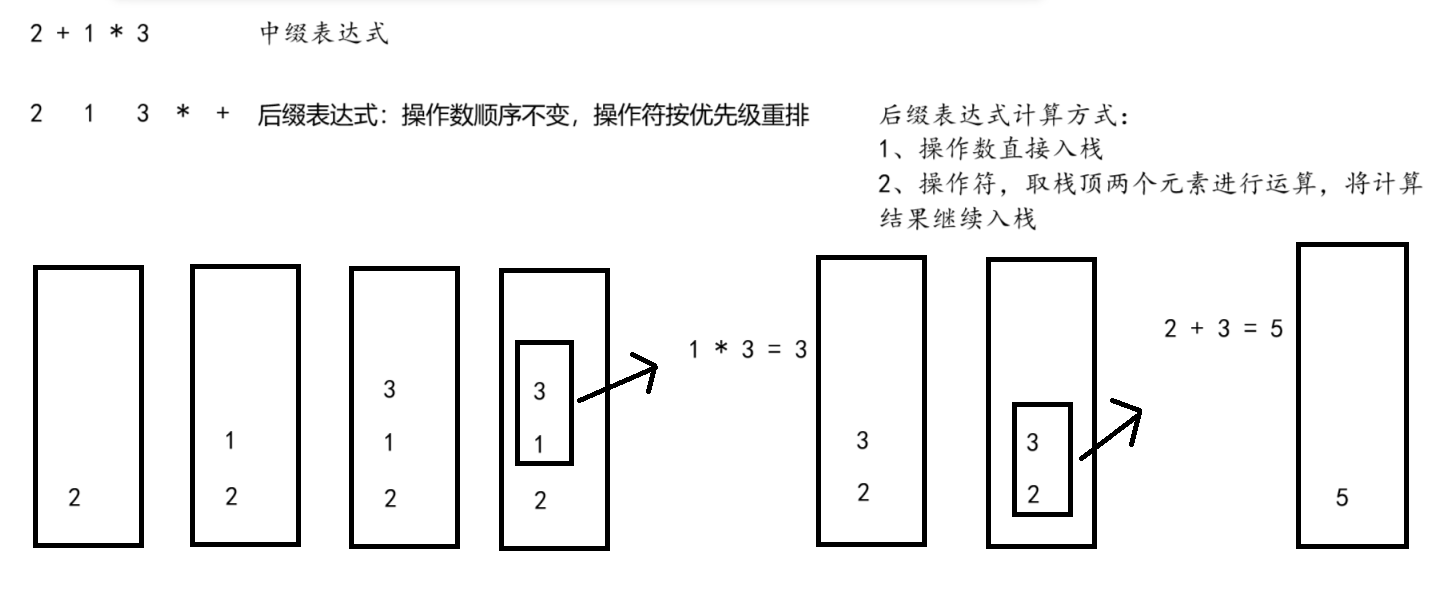
【代码示例】
cpp
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(auto& e: tokens)
{
//操作符 取栈顶两个元素进行运算,运算结果入栈
if(e == "+" ||e== "-" || e== "*" || e== "/")
{
int right = st.top();
st.pop();
int left = st.top();
st.pop();
switch(e[0])
{
case '+':
st.push(left+right);
break;
case '-':
st.push(left-right);
break;
case '*':
st.push(left*right);
break;
case '/':
st.push(left/right);
break;
}
}
else//操作数直接入栈
{
//字符串转整型
st.push(stoi(e));
}
}
return st.top();
}
};4、用栈实现队列
【题目链接】: https://leetcode.cn/problems/implement-queue-using-stacks/

【思路分析】
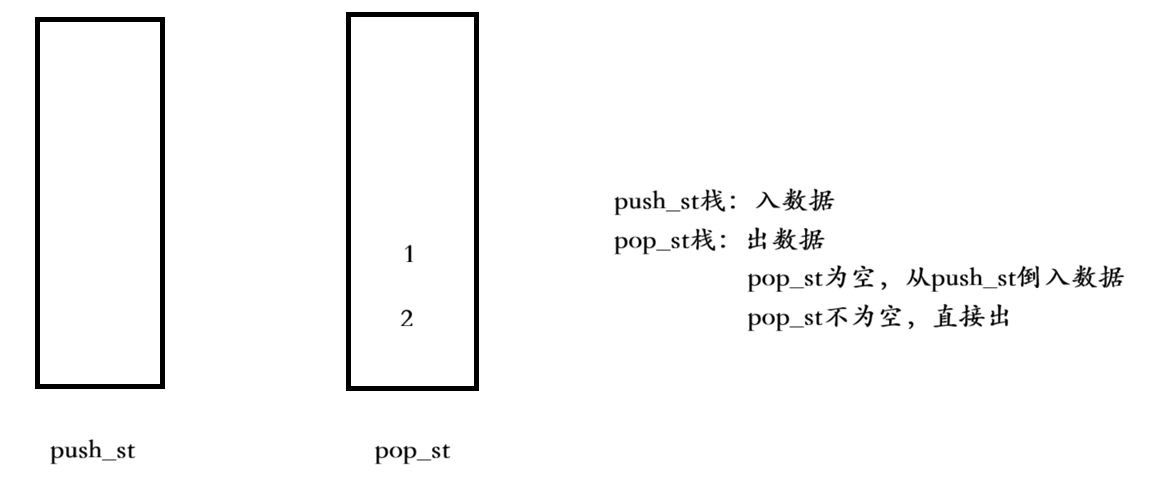
【代码示例】
cpp
class MyQueue {
public:
// 构造函数:编译器自动生成,初始化两个空栈
MyQueue() {
}
// 入队操作:将元素x加入队列(直接压入push_st栈)
void push(int x) {
push_st.push(x);
}
// 出队操作:移除并返回队列的队头元素
int pop() {
// 1. 若pop_st为空,将push_st中的所有元素倒序转移到pop_st中
// 转移后pop_st的栈顶即为队列的队头元素
if(pop_st.empty())
{
while(!push_st.empty())
{
int top = push_st.top();
push_st.pop();
pop_st.push(top);
}
}
// 2. 保护逻辑:若两个栈都为空(队列空),返回0
if(pop_st.empty())
{
return 0;
}
// 3. 弹出pop_st栈顶(即队列队头)并返回
int top = pop_st.top();
pop_st.pop();
return top;
}
// 查看队头元素:返回队列的队头元素(不移除)
int peek() {
// 1. 若pop_st为空,将push_st中的所有元素倒序转移到pop_st中
if(pop_st.empty())
{
while(!push_st.empty())
{
int top = push_st.top();
push_st.pop();
pop_st.push(top);
}
}
// 2. 保护逻辑:若两个栈都为空(队列空),返回0
if(pop_st.empty())
{
return 0;
}
// 3. 返回pop_st栈顶(即队列队头),不弹出元素
int top = pop_st.top();
return top;
}
// 判断队列是否为空:两个栈都为空时,队列才为空
bool empty() {
return push_st.empty() && pop_st.empty();
}
private:
stack<int> push_st; // 入数据栈:专门接收新加入队列的元素
stack<int> pop_st; // 出数据栈:专门用于弹出/查看队列的队头元素
};
5、用队列实现栈
【题目链接】: https://leetcode.cn/problems/implement-stack-using-queues/

【思路分析】
push 操作:始终向 "非空的队列" 中加入元素(保证新元素在队列尾部,最终成为栈顶);
pop 操作:将非空队列的元素(除了最后一个)全部倒入空队列,剩下的最后一个元素就是栈顶,直接弹出即可。
【代码示例】
cpp
class MyStack {
public:
MyStack() {
}
// 入栈:压入非空队列(双空则入q2)
void push(int x) {
if(!q1.empty())
{
q1.push(x);
}
else
{
q2.push(x);
}
}
int pop() {
// 情况1:q1为空,处理q2
if(q1.empty())
{
// 将q2前n-1个元素导入q1,保留最后一个作为栈顶
while(q2.size()>1)
{
int front = q2.front();
q2.pop();
q1.push(front);
}
// 取出并弹出q2中仅剩的栈顶元素
int ret = q2.front();
q2.pop();
return ret;
}
// 情况2:q2为空,处理q1(逻辑同q2)
else
{
while(q1.size()>1)
{
int front = q1.front();
q1.pop();
q2.push(front);
}
int ret = q1.front();
q1.pop();
return ret;
}
// 栈空保护:两个队列都为空时返回0(注:此语句无法执行,已提前在top()处理)
if(empty())
{
return 0;
}
}
// 取栈顶:返回非空队列的队尾,栈空返回0
int top() {
if(!q1.empty())
{
return q1.back();
}
else if(!q2.empty())
{
return q2.back();
}
else
{
return 0;
}
}
// 判断栈空:两个队列都为空即为栈空
bool empty() {
return q1.empty() && q2.empty();
}
queue<int> q1;
queue<int> q2;
};