41-parse的实现原理&有限状态机

parse 的实现原理

有限状态机 finite state machine

读取一组输入，然后根据这些输入来更改为不同的状态

js 复制代码

state1----->  state2
    `------>  state3

简述 parse 的过程

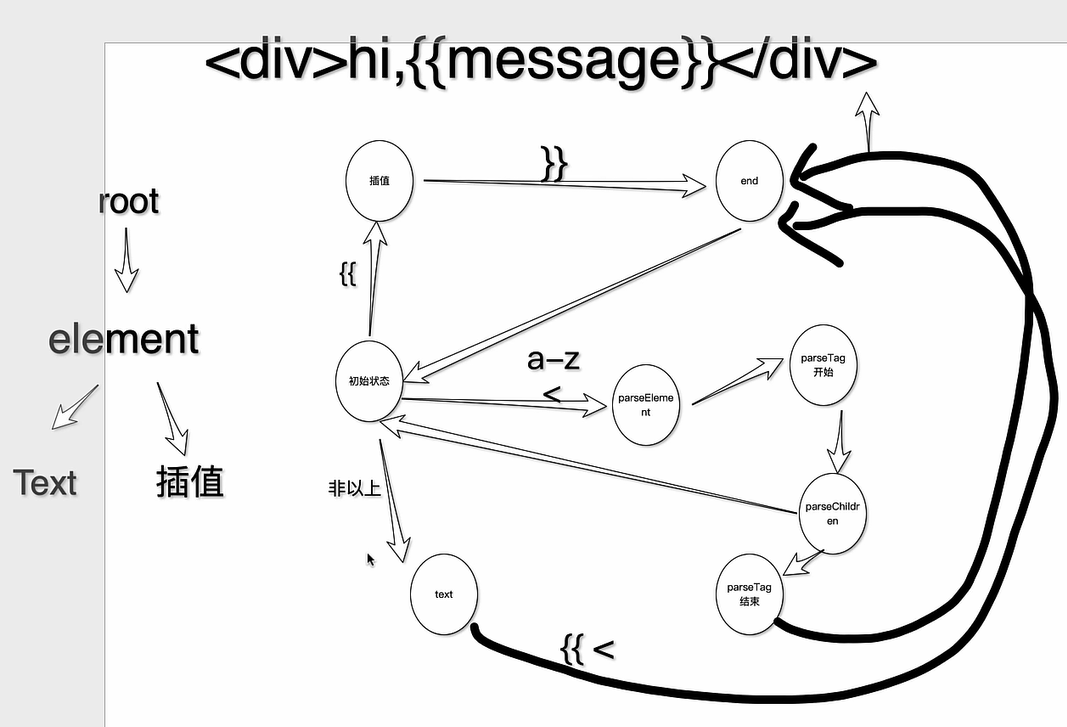
初始状态-----}}-----> 插值 ---> end ↓
-----< a-z-----> parseElement ----> parseTag 开始 ---> parseChildren(循环) ---> parseTag 结束 ↓ -----非以上是text-----> parseText ↓
结束

解析插值语法
解析 < a-z 标签语法
解析除以上两种语法外的 text 语法

状态机经常被用在词法语法解析的场景
使用有限状态机实现正则表达式功能

js 复制代码

function test(string) {
  function waitForA(char) {
    if (char === 'a') {
      return waitForB
    }
    return waitForA
  }

  function waitForB(char) {
    if (char === 'b') {
      return waitForC
    }
    return waitForA
  }


  function waitForC(char) {
    if (char === 'c') {
      return end
    }
    return waitForA
  }
  function end() {
    return end
  }

  let currentState = waitForA
  for (let i = 0; i < string.length; i++) {
    let nextState = currentState(string[i])
    currentState = nextState
    if(currentState === end) {
      return true
    }
  }
  return false
}
console.log(test('abc')); // true
    
console.log(test('acc')); // false

console.log(test('labcfdds')); // true

获取匹配的 "abc" 的下标

js 复制代码

function test(string) {
  let startIndex // ✅
  let endIndex // ✅
  let i  // ✅
  let result = []
  function waitForA(char) {
    if (char === 'a') {
      startIndex = i // ✅
      return waitForB
    }
    return waitForA
  }

  function waitForB(char) {
    if (char === 'b') {
      return waitForC
    }
    return waitForA
  }

  function waitForC(char) {
    if (char === 'c' || char === 'd') {
      endIndex = i // ✅ 
      return end
    }
    return waitForA
  }

  function end() {
    return end
  }

  let currentState = waitForA
  for (i = 0; i < string.length; i++) {
    let nextState = currentState(string[i])
    currentState = nextState
    if(currentState === end) { // ✅
      console.log(startIndex, 'startIndex');  // ✅
      console.log(endIndex, 'endIndex'); // ✅
      result.push({ // ✅
        start: startIndex,
        end: endIndex
      })
      currentState = waitForA   // ✅  相当于结束回到初始状态, 这样能够下次循环继续走流程检验，否则会一直处在 end 状态
      // return true // ✅
    }
  }
  // return false
}
// console.log(test('abc')); // true
    
// console.log(test('acc')); // false

console.log(test('labcfabcdds')); // true

实现 /ab $cd$ /

js 复制代码

function waitForC(char) {
  if (char === 'c' || char === 'd') {
    endIndex = i 
    return end
  }
  return waitForA
}

有限状态机配图