概率图模型(PGM)
含义：用图来表示变量概率依赖关系
三步曲：
- 表示 representation（建模为图结构）
- 推断 inference（计算概率）
- 学习 learning（估计模型参数）
有向图
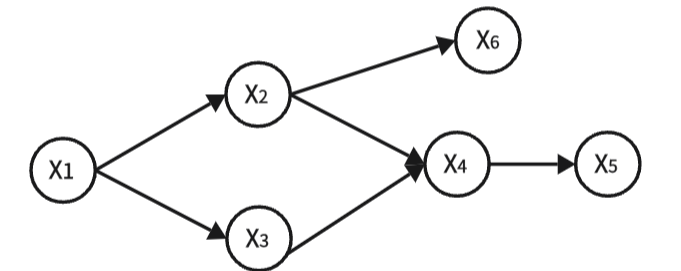
- 节点对应连续或离散随机变量
- 有向边连接父节点
- 有向边表示条件概率分布
- 不存在回路，又称为有向无环图模型（DAG）
公式：
-
：节点
-
每一项都是一个条件概率分布（CPD）
无向图
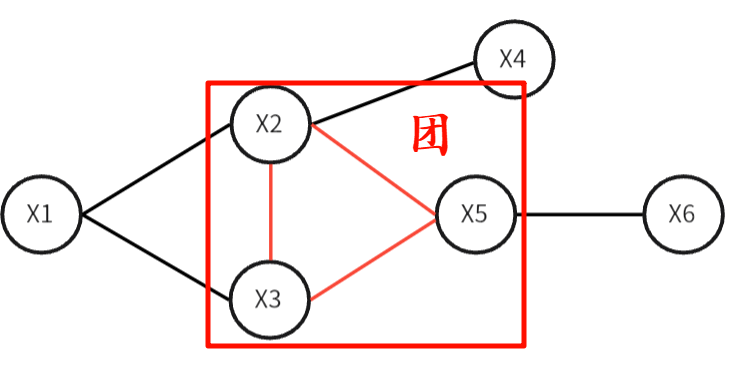
- 节点对应连续或离散随机变量
- 边表示依赖关系
- 任意两节点都有连接，则该节点子集为团(clique)
- 联合概率分布能够基于团分解（实现简化）
公式：
-
-
-
相互转换
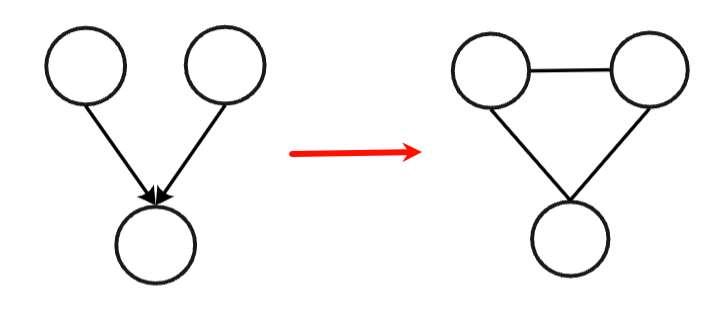
有向图转换为无向图
- 对"共同子节点"的父节点连边（道德化）
- 去掉所有箭头方向
- 得到无向图（MRF）
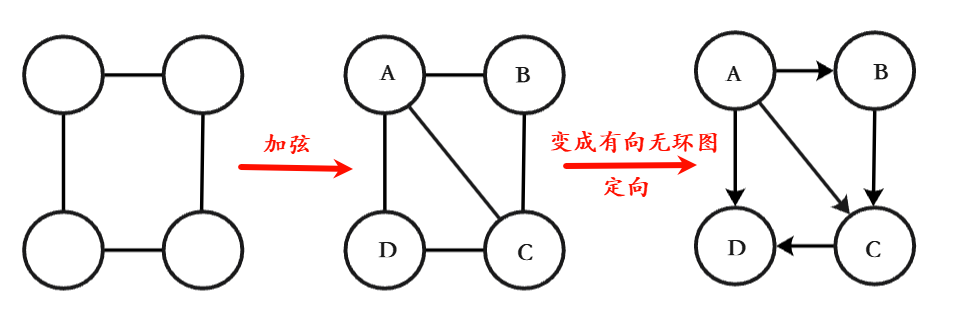
无向图转换为有向图
弦： 在一个环 里，连接两个不相邻节点的那条边，就叫弦
- 检查无向图是否为弦图，任意长度 ≥ 4 的简单环，都必须存在一条"弦"
- 给节点设定一个序号（方便后续定向）
- 节点连线并给边定向（也可以按照**所有边都从"后出现的节点"指向"先出现的节点"**的规则）
推断方法
- 精确推断：变量消去法、信念传播法
- 近似推断：MCMC采样法、变分推断(Variational inference)
隐马尔可夫模型(HMM)
HMM 用一个"看不见的状态序列"来生成"看得见的观测序列"，并假设状态满足马尔可夫性、观测只依赖当前状态。
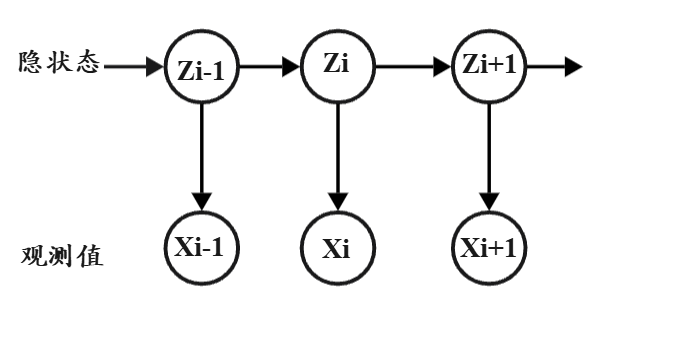
存在隐状态序列
- 数据是由不可直接观测的状态生成的
- 我们只能看到状态的"外在表现"
例子：
- 真实天气（隐）→ 是否下雨/带伞（观测）
- 人的行为意图（隐）→ 传感器数据（观测）
近似推断----EM算法参数估计
期望最大化算法（Expectation Maximization）
目标：估计模型参数 θ，使观测数据的似然最大
Jensen不等式（函数的期望与期望的函数的关系）：
算法思想：
EM 算法使用Jenson不等式 ，将难以直接优化的对数似然函数转化为一个可优化的下界 ，并通过交替最大化该下界实现参数估计
先"猜"隐变量的分布(公式中的
E步骤：估计隐变量
- q分布不变
- 最大化Z
M步骤：更新参数
- Z不变
- q最大化寻优
隐马尔可夫模型代码实现
基本假设
观测独立性假设
当前观测只由当前隐状态决定，与其他状态和观测无关。
齐次马尔科夫假设
当前隐状态只依赖于前一个隐状态，与更早的状态无关。
简单的隐马尔可夫模型
问题：已知小明连续五次考试成绩：A+,B,A-,C+,A，求小明每次考试的状态
存在三种状态(隐状态)：认真复习(S1)，简单复习(S2)，没有复习(S3)
考试成绩--->观测数据：A+:o1,A:o2,A-:o3,B+:o4,B:o5,B-:o6,C+:o7,C:o7,C-:o9
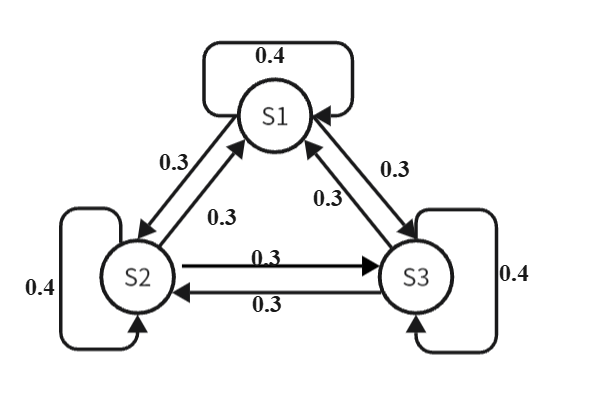隐状态转移概率 
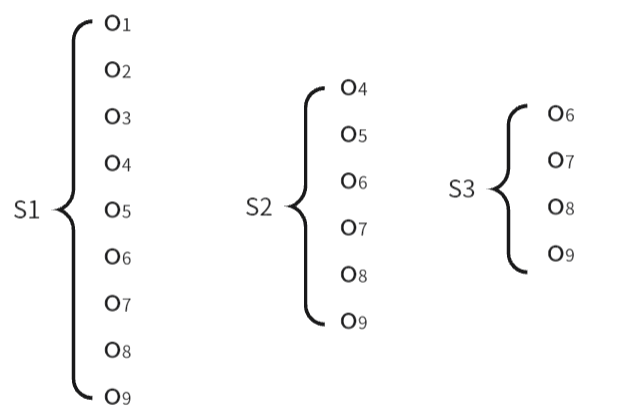隐状态对应观测结果
状态初始概率：
状态转移矩阵：
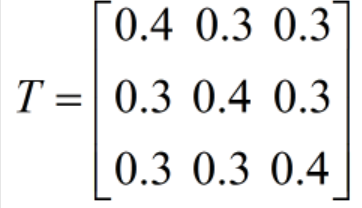
发射概率矩阵（在某个隐状态下，产生各个观测值的概率分布）：
隐马尔可夫模型推理
|---------|---------------------------------------|---------------------------------------|---------------------------------------|---------------------------------------|---------------------------------------|
| 时间 | |
|
|
|
|
| 成绩 | A+ | B | A- | C+ | A |
| 观测 | |
|
|
|
|
| 隐状态 | |
|
|
|
|
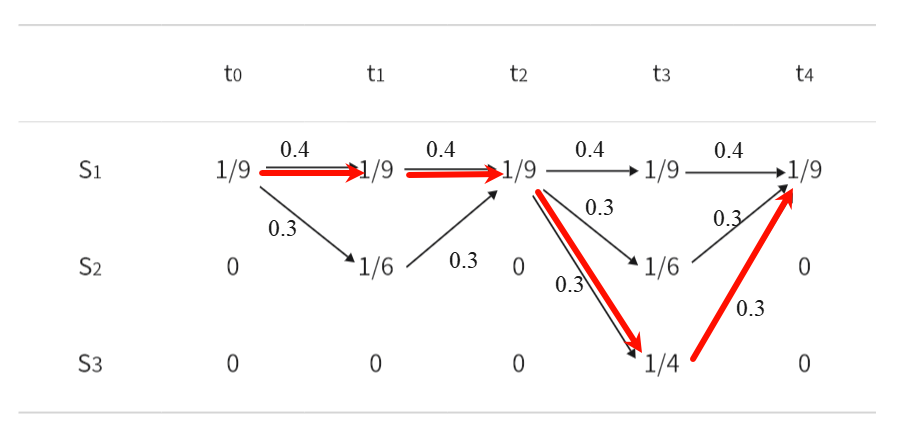
- t0,t2,t4时刻产生的观测数据只能由状态S1产生所以此时三个时刻对应的状态为S1
- t1时刻观测值为o5，可能由S1，S2产生,分析t0->t2时刻：
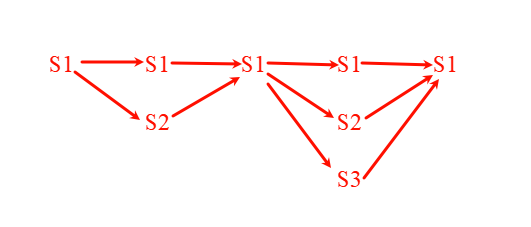
①S1->S1->S1概率：
②S1->S2->S1概率：
对比分析①的概率大于②的概率，则选择①
- 同理，继续分析下面的状态
- 最终状态：
代码实现
python
import numpy as np
state = np.array(['认真复习','简单复习','没有复习'])
grade = np.array(['A+','A','A-','B+','B','B-','C+','C','C-'])
n_state = len(state)
m_grade = len(grade)
pi = np.ones(n_state)/n_state
t = np.array([
[0.4,0.3,0.3],
[0.3,0.4,0.3],
[0.3,0.3,0.4]
])
e = np.zeros([3,9])
e[0,:9]=1/9
e[1,3:9]=1/6
e[2,5:9]=1/4
from hmmlearn.hmm import CategoricalHMM
hmm = CategoricalHMM(n_state)
hmm.startprob_ = pi
hmm.transmat_ = t
hmm.emissionprob_ = e
hmm.n_features = 9
datas = np.array([0,4,2,6,1])
datas = np.expand_dims(datas,axis=1)
states = hmm.predict(datas)优缺点和适用条件
|---------|----------------------------|--------------------|-------------------------|
| 方法 | 优点 | 缺点 | 应用 |
| HMM | 很多场景下可以大大简化条件概率计算 | 应用范围比较窄，主要用于时序数据建模 | 语音识别 故障检测 行为识别 |
| 概率图 | 思路清晰：建模表示+推断学习 可解释性强，白盒子模型 | 推断和学习复杂，高维数据处理困难 | 动态化结构学习 非参数化建模 深度学习+概率图 |