【人工智能引论期末复习】第4章机器学习3-无监督学习

一、无监督学习概述（填空题高频）

两类任务：
1. 化繁为简：聚类、降维
2. 无中生有：生成模型
聚类：将相似样本划分为同一类
降维：将高维数据映射到低维空间，保留主要信息
分布式表示：用向量描述对象，每一维代表某种属性

二、K均值聚类（重点）

1. 算法流程（简答题高频）

初始化聚类质心（随机选择K个）
将每个样本分配到最近的质心（欧氏距离）
根据聚类结果更新质心（取类内均值）
重复步骤2-3直到质心不变或达到迭代上限

2. 目标函数

最小化类内方差（类内距离最小）
最大化类间距离（类间距离最大）

3. 优缺点

优点：简单、高效、适用于大样本
缺点：
- 需预设K值
- 对初始质心敏感
- 对离群点敏感
- 假设各维度重要性相同（欧氏距离）

4. K-means vs KNN

K-means：无监督聚类算法
KNN：监督分类算法，基于最近邻投票

三、主成分分析（PCA）（重点）

1. 目标

最大化投影后方差，保留最多信息
降维后保持原始数据结构

2. 步骤（填空题/简答题）

中心化（零均值化）
计算协方差矩阵
特征值分解，排序特征值
取前L个最大特征值对应的特征向量组成投影矩阵

3. 协方差与相关系数

协方差：衡量两个变量的总体误差
相关系数：标准化后的协方差，范围[-1,1]

4. PCA vs LDA

PCA：无监督，最大化方差
LDA：有监督，最大化类间距离、最小化类内距离

四、其他降维方法（选择题/填空题）

1. 非负矩阵分解（NMF）

将非负矩阵分解为两个非负矩阵乘积
适用于图像、文本等非负数据

2. 多维尺度法（MDS）

保持样本间距离不变
适用于距离已知的数据

3. 局部线性嵌入（LLE）

保持局部邻域关系
适用于非线性流形数据

五、特征人脸方法（Eigenface）

本质：PCA在人脸识别中的应用
步骤：
1. 人脸图像向量化
2. 中心化
3. PCA降维
4. 用特征脸表示新人脸
特点：子空间算法，用于人脸检测与识别

六、潜在语义分析（LSA）

目标：挖掘单词-文档之间的语义关系
方法：对"单词-文档"矩阵进行SVD分解
作用：消除同义词、多义词影响，提取语义特征

七、期望最大化算法（EM）（重点）

1. 适用问题

含有隐变量的参数估计问题
例如：混合高斯模型、隐马尔可夫模型

2. 算法步骤（填空题/简答题）

E步：基于当前参数估计隐变量分布
M步：基于隐变量分布更新参数
交替迭代直到收敛

3. K-means是EM的特例

E步：分配样本到最近质心
M步：更新质心

八、高频考点总结

考点	出题形式	复习重点
K均值流程	简答题、填空	四步流程、终止条件
PCA步骤	填空、简答	中心化、协方差、特征值分解
聚类 vs 分类	选择题	K-means vs KNN
降维方法比较	选择题、填空	PCA、LDA、MDS、LLE
EM算法思想	填空、简答	E步、M步、隐变量
特征人脸方法	填空	基于PCA、用于人脸识别

九、可能出题方向

填空题示例：

K均值聚类使用________距离进行样本分配。
PCA的目标是最大化投影后的________。
EM算法中，E步用于估计________。

选择题示例：

下列哪种降维方法是有监督的？
K-means对什么敏感？
潜在语义分析使用什么分解方法？

简答题示例：

简述K均值聚类算法的流程。
说明PCA与LDA的区别。
解释EM算法的基本思想与步骤。

🔢 典型计算题（附解答）

📘 综合题（跨章节）

题目4：聚类与降维比较

说明：

假设有一个高维数据集，你希望将其可视化到二维平面。

请回答：

你会选择PCA还是t-SNE？为什么？
如果你希望保持局部结构，应选择哪种方法？
K均值能否用于降维？为什么？

📄 模拟试题（第5章专项）

一、填空题（每空1分，共10分）

K均值聚类使用________距离进行样本分配。
PCA的目标是最大化投影后的________。
EM算法中，E步用于估计________。
特征人脸方法是________在人脸识别中的应用。
潜在语义分析使用________分解方法。
聚类属于无监督学习中的________任务。
降维后保持样本间距离不变的方法是________。
非负矩阵分解要求矩阵元素________。
K-means对________敏感。
LDA是有监督的降维方法，目标是最大化________。

二、选择题（每题2分，共10分）

下列哪种降维方法是有监督的？
- A. PCA
- B. LDA
- C. MDS
- D. LLE
K-means聚类算法对什么最敏感？
- A. 数据量大小
- B. 初始聚类中心
- C. 数据维度
- D. 迭代次数
潜在语义分析主要用于：
- A. 图像分类
- B. 文本语义提取
- C. 语音识别
- D. 推荐系统
EM算法适用于：
- A. 含有隐变量的参数估计
- B. 线性回归
- C. 决策树构建
- D. 支持向量机
下列哪个不是PCA的步骤？
- A. 中心化
- B. 计算协方差矩阵
- C. 梯度下降优化
- D. 特征值分解

三、简答题（每题5分，共10分）

简述K均值聚类算法的流程，并说明其优缺点。
说明PCA与LDA的区别。

✅ 参考答案

典型计算题答案

题目4：

选择t-SNE，因为更适合可视化，能保持局部结构。
保持局部结构选LLE或t-SNE。
K均值不能降维，它只聚类，不改变维度。

模拟试题答案

一、填空题

欧氏
方差
隐变量分布
PCA
SVD
聚类
MDS
非负
初始聚类中心
类间距离/类内距离比值

二、选择题

三、简答题

流程：初始化中心 → 分配样本 → 更新中心 → 迭代至收敛。
优点：简单、高效。
缺点：需预设K、对初始中心敏感、假设各维同等重要。
PCA ：无监督，最大化方差，保留全局结构。
LDA：有监督，最大化类间距离、最小化类内距离，适用于分类。

🤖 人工智能导论期末模拟卷（含答案）

一、填空题（每空1分，共20分）

在机器学习中，如果模型在训练集上表现很好但在测试集上表现差，这种现象称为________。
逻辑回归使用________函数将输出映射到(0,1)区间。
决策树划分时，C4.5算法使用________作为划分指标。
SVM中用于处理线性不可分问题的技术是________。
AdaBoost中，错分样本的权重会________。
生成模型学习的是________概率分布。
K均值聚类使用________距离进行样本分配。
PCA的目标是最大化投影后的________。
EM算法中，E步用于估计________。
特征人脸方法是________在人脸识别中的应用。
潜在语义分析使用________分解方法。
在强化学习中，Q学习是基于________的算法。
神经网络通过激活函数实现________映射。
MiniMax算法的时间复杂度为________。
蒙特卡洛树搜索中，UCB算法选择________大的动作。
根据大数定律，可以用样本均值估计总体，要求变量独立________分布。
贝叶斯网络用________图表示概率依赖关系。
Transformer引入了________机制。
安全子博弈得到的结果一定不差于全局的________。
在分组比较时每组表现都更好但在总体上表现更差，这是________。

二、选择题（每题2分，共20分）

下列哪个是判别模型？
- A. 朴素贝叶斯
- B. 隐马尔可夫模型
- C. 逻辑回归
- D. 高斯混合模型
决策树划分时，CART算法使用哪个指标？
- A. 信息增益
- B. 信息增益率
- C. 基尼系数
- D. 交叉熵
在SVM中，支持向量是指：
- A. 所有训练样本
- B. 被错误分类的样本
- C. 距离超平面最近的样本
- D. 随机选择的样本
AdaBoost属于哪种集成学习策略？
- A. Bagging
- B. Boosting
- C. Stacking
- D. Blending
下列哪种降维方法是有监督的？
- A. PCA
- B. LDA
- C. MDS
- D. LLE
K-means聚类算法对什么最敏感？
- A. 数据量大小
- B. 初始聚类中心
- C. 数据维度
- D. 迭代次数
潜在语义分析主要用于：
- A. 图像分类
- B. 文本语义提取
- C. 语音识别
- D. 推荐系统
EM算法适用于：
- A. 含有隐变量的参数估计
- B. 线性回归
- C. 决策树构建
- D. 支持向量机
逻辑回归的损失函数是：
- A. 均方误差
- B. 交叉熵
- C. 绝对值误差
- D. 铰链损失
下列哪个不是PCA的步骤？
- A. 中心化
- B. 计算协方差矩阵
- C. 梯度下降优化
- D. 特征值分解

三、简答题（每题6分，共30分）

简述逻辑回归与线性回归的区别。
说明生成模型与判别模型的区别，并各举一个例子。
简述K均值聚类算法的流程。
解释SVM中"最大间隔"的含义及其优势。
说明PCA与LDA的区别。

四、计算题（每题10分，共20分）

题目1：决策树信息增益计算

已知数据集：

天气	温度	湿度	风力	是否打球
晴	高	高	弱	否
晴	高	高	强	否
阴	高	高	弱	是
雨	中	高	弱	是
雨	低	中	弱	是
雨	低	中	强	否
阴	低	中	强	是
晴	中	高	弱	否

计算"天气"属性的信息增益（使用熵公式）。

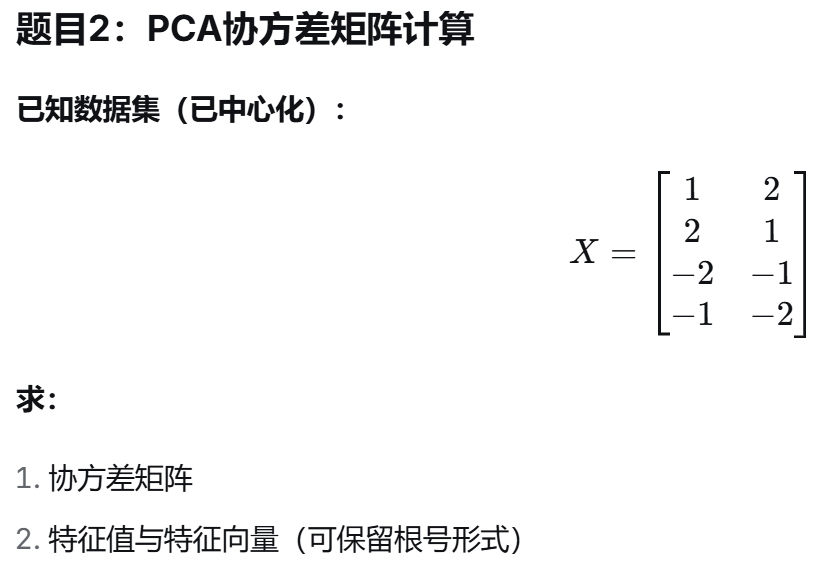
题目2：PCA计算

已知数据集（已中心化）：

X=[2112−1−2−2−1]X=21−1−212−2−1

求：

协方差矩阵
第一主成分方向（单位向量）

五、论述题（10分）

题目：

结合机器学习理论，论述"过拟合"与"欠拟合"的产生原因、表现特征及常用解决方法，并说明在模型选择中如何平衡二者。

✅ 参考答案

一、填空题

过拟合
Sigmoid
信息增益率
核函数
增加
联合
欧氏
方差
隐变量分布
PCA
SVD
价值
非线性
O(b^d)
置信上限
同
有向无环
自注意力
近似解
辛普森悖论

二、选择题

C 2. C 3. C 4. B 5. B
B 7. B 8. A 9. B 10. C

三、简答题（要点）

逻辑回归 vs 线性回归
- 逻辑回归：分类任务，输出概率，使用Sigmoid函数
- 线性回归：回归任务，输出连续值
生成模型 vs 判别模型
- 生成模型：学习联合概率分布P(X,Y)，如朴素贝叶斯
- 判别模型：学习条件概率P(Y|X)或决策函数，如SVM
K均值流程

初始化中心 → 分配样本 → 更新中心 → 迭代至收敛
SVM最大间隔

使两类样本到超平面的最小距离最大，提高泛化能力，减少过拟合
PCA vs LDA
- PCA：无监督，最大化方差，保留全局结构
- LDA：有监督，最大化类间距离、最小化类内距离，用于分类

四、计算题

题目1：

总熵 H(D) = 1（正负样本各4个）
按天气划分：
- 晴：3个否 → 熵=0
- 阴：2个是 → 熵=0
- 雨：2是1否 → 熵≈0.918
信息增益 IG = 1 - (3/8×0 + 2/8×0 + 3/8×0.918) ≈ 0.311

题目2：

协方差矩阵：

C=13[108810]C=31[108810]

最大特征值 λ₁ = 6，特征向量 v₁ = [1,1]^T

单位化：u₁ = [√2/2, √2/2]^T

五、论述题（要点）

过拟合：

原因：模型复杂、训练数据少、噪声多
表现：训练误差小、测试误差大
解决：正则化、增加数据、简化模型、早停、交叉验证

欠拟合：

原因：模型简单、特征不足、训练不充分
表现：训练误差大、测试误差大
解决：增加特征、使用更复杂模型、延长训练时间

平衡策略：

使用验证集调参
采用偏差-方差权衡
选择合适复杂度模型
集成学习方法

备注： 本模拟卷基于《2025回忆卷》风格与第4-5章内容设计，可作为考前冲刺使用。如需更多章节覆盖或专项练习，可继续提出需求。

题目4：聚类与降维比较说明：假设有一个高维数据集，你希望将其可视化到二维平面。请回答：你会选择PCA还是t-SNE？为什么？如果你希望保持局部结构，应选择哪种方法？ K均值能否用于降维？为什么？

题目4：聚类与降维比较参考答案

问题1：你会选择PCA还是t-SNE？为什么？

答案：

我会选择t-SNE，因为：

可视化效果更优：
- t-SNE专为高维数据可视化设计，能更好地保持数据点之间的局部相似性关系
- PCA主要保留全局方差结构，对于复杂的流形结构可视化效果有限
保持局部结构能力：
- t-SNE通过概率分布建模，强调保持近邻点的相对位置
- PCA是线性方法，无法捕捉非线性关系
聚类模式显现：
- t-SNE通常能产生更清晰的聚类分离
- PCA可能将不同类别混在一起，尤其是当类别差异不是数据主要方差来源时
适用场景：
- 对于探索性数据分析和发现潜在模式，t-SNE更适合
- 如果需要可解释的主成分方向或快速降维，PCA更合适

问题2：如果你希望保持局部结构，应选择哪种方法？

答案：

应选择t-SNE，原因如下：

设计目标不同：
- t-SNE：专门设计为保持局部邻域关系，最小化高维和低维空间中概率分布的KL散度
- PCA：设计为最大化全局方差，可能牺牲局部结构
流形学习能力：
- t-SNE属于非线性降维方法，能处理复杂的流形结构
- PCA是线性方法，假设数据位于线性子空间
替代方案：
- 如果需要保持局部结构，还可考虑LLE（局部线性嵌入） 或Isomap
- 这些方法都是专门为保持局部或全局拓扑结构设计的
权衡考虑：
- t-SNE计算成本较高，对超参数（困惑度perplexity）敏感
- 但对于可视化，通常值得付出这些代价

问题3：K均值能否用于降维？为什么？

答案：
K均值不能直接用于降维，原因如下：

本质不同：
- K均值是聚类算法：将数据划分为K个簇，输出是簇标签
- 降维算法：将高维数据映射到低维空间，输出是低维坐标
维度不变性：
- K均值处理后，数据维度不变（仍是原始维度）
- 只是多了个簇标签，但特征空间维度未减少
信息损失方式不同：
- 聚类：用簇质心代表所有成员，损失了类内差异信息
- 降维：保留了主要变异方向，损失的是次要成分
间接使用方式 ：

虽然K均值不能直接降维，但可以：
- 聚类后可视化：用簇标签作为一维离散特征，但这会丢失大量信息
- 与降维结合：先降维再聚类，或先用聚类提取特征再可视化
对比PCA：
- PCA：将d维数据投影到k维子空间（k<d），维度降低
- K均值：将n个样本分配到k个簇，样本数不变，维度不变

结论：

K均值是聚类方法，不是降维方法。对于降维任务，应使用专门的降维算法如PCA、t-SNE、LLE等。

天气	温度	湿度	风力	是否打球
晴	高	高	弱	否
晴	高	高	强	否
阴	高	高	弱	是
雨	中	高	弱	是
雨	低	中	弱	是
雨	低	中	强	否
阴	低	中	强	是
晴	中	高	弱	否

天气	温度	湿度	风力	是否打球
晴	高	高	弱	否
晴	高	高	强	否
阴	高	高	弱	是
雨	中	高	弱	是
雨	低	中	弱	是
雨	低	中	强	否
阴	低	中	强	是
晴	中	高	弱	否

【人工智能引论期末复习】第4章 机器学习3-无监督学习

一、无监督学习概述（填空题高频）

二、K均值聚类（重点）

1. 算法流程（简答题高频）

2. 目标函数

3. 优缺点

4. K-means vs KNN

三、主成分分析（PCA）（重点）

1. 目标

2. 步骤（填空题/简答题）

3. 协方差与相关系数

4. PCA vs LDA

四、其他降维方法（选择题/填空题）

1. 非负矩阵分解（NMF）

2. 多维尺度法（MDS）

3. 局部线性嵌入（LLE）

五、特征人脸方法（Eigenface）

六、潜在语义分析（LSA）

七、期望最大化算法（EM）（重点）

1. 适用问题

2. 算法步骤（填空题/简答题）

3. K-means是EM的特例

八、高频考点总结

九、可能出题方向

填空题示例：

选择题示例：

简答题示例：

🔢 典型计算题（附解答）

📘 综合题（跨章节）

题目4：聚类与降维比较

📄 模拟试题（第5章专项）

一、填空题（每空1分，共10分）

二、选择题（每题2分，共10分）

三、简答题（每题5分，共10分）

✅ 参考答案

典型计算题答案

模拟试题答案

🤖 人工智能导论期末模拟卷（含答案）

一、填空题（每空1分，共20分）

二、选择题（每题2分，共20分）

三、简答题（每题6分，共30分）

四、计算题（每题10分，共20分）

五、论述题（10分）

✅ 参考答案

一、填空题

二、选择题

三、简答题（要点）

四、计算题

五、论述题（要点）

题目4：聚类与降维比较 参考答案

问题1：你会选择PCA还是t-SNE？为什么？

问题2：如果你希望保持局部结构，应选择哪种方法？

问题3：K均值能否用于降维？为什么？

【人工智能引论期末复习】第4章机器学习3-无监督学习

题目4：聚类与降维比较参考答案

天气	温度	湿度	风力	是否打球
晴	高	高	弱	否
晴	高	高	强	否
阴	高	高	弱	是
雨	中	高	弱	是
雨	低	中	弱	是
雨	低	中	强	否
阴	低	中	强	是
晴	中	高	弱	否