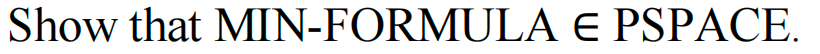✅西电计算复杂性理论期末笔记

cur oh4的重点；助教的回答；所有题再过一遍；笔记；其他课件；标记🍑的点和同学讨论，看看大家怎么认为这个点对应什么；第七次作业题；lecture 5

✅：lecture4

计复期末划重点

规约过程的关键可以总结为：给出构造方式，证明构造过程的开销符合预期，证明规约前后二者等价

规约：核心思想：构造&变形，使得二者，你有解，则我有解，反之亦然

题目不超过10道（1选择，其余是大题）

⚠️：选择题是单选还是多选需要自己分析；

⚠️：大题是问答题（Q&A）形式（一般是概念结合实际例子）；英文作答（关键概念词必须写对）；

⚠️：不允许携带相关资料&词典；考试没那么难。

主要考点

？✅1.P，NP，PSPACE，coNL/NL；概念之间是什么关系，为什么**（大题的原因分析很重要）**

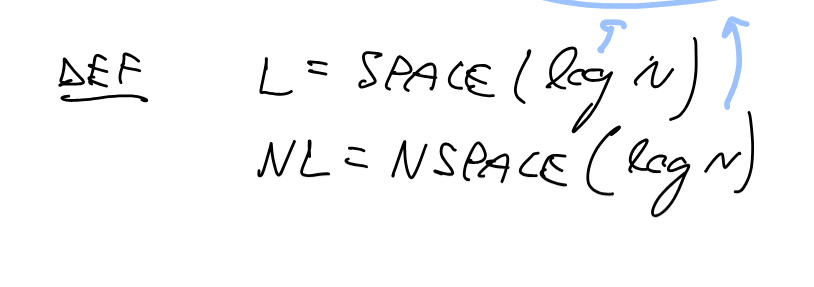
NL = coNL（immerman-szelepcsenyi THM）教授只提到这个fact，没有细讲

：只需要证明coPATH问题（两个节点之间没有路径）属于NL

证明从s到t没有可达路径，遍历所有节点，讨论是否从s可达，问题就变成了n个PATH问题，但是利用空间复用规则，求解使用的空间也是log级别的，只需要存下可达节点的索引

**NL包含于P：✅**消耗空间是S(n)的图灵机最多消耗的时间是2^O(f(n))，因此对数空间消耗的时间是多项式级别的。

⚠️❌不可以反过来说，消耗的时间是T的TM所消耗的空间至多是log(T)

P包含于NP： If you can directly calculate the answer (P), you can certainly verify a given answer (NP)

NP包含于NPSPACE： 为了模拟 NP 中的++非确定性猜测++ ，你可以用确定性算法尝试所有可能的赋值或路径 。虽然这需要指数级的 时间，但只要你一次只尝试一种情况，用完后释放空间再试下一种，总空间消耗依然是多项式级别的 。To simulate nondeterministic guessing in NP, you can use a deterministic algorithm to try all possible assignments or paths. Although this requires exponential time, as long as you only try one case at a time and release the space before trying the next, the total space consumption remainsat a polynomial level.【空间复用规则Spatial reuse rules】

🍑✅2.图灵机的空间/时间复杂度关联推导（作业中有）

TM功能：指针在纸带上移动 和修改某一个位置的内容

**描述：**进行什么操作，如果怎么样就accept，怎么样就reject

✅图灵机：

读写头，纸带，有限控制器

PS：单带图灵机一共只有一个带子，承担所有功能

✅多带图灵机

多带の基本结构：

• 拥有 k条带子（k≥1），每条带子无限长，划分为单元格
• 每条带子有一个独立的读写头，可以左右移动
• 一个有限状态控制器，根据当前状态和各读写头读取的符号决定下一步动作
• 通常约定第一条带子为输入带 （只读），最后一条带子为输出带（只写），中间为工作带（读写）

性质：若多带机在 T(n) 时间内解决问题，
则存在单带机在 O(T(n)²) 时间内解决同一问题。

证明：为了在一条带子上存放 k 条带子的信息，单带图灵机通常会将这 k 条带子的内容"分段"存放，并用特殊的定界符（如 #）隔开。同时，为了记住多带机每个头的位置，单带机需要在对应的字符上做特殊标记（比如把 a 标记为 \\dot{a}）。【虚拟读写头】

多带机运行t步，每一步单带机都要扫描全带，找齐 k 个虚拟头的位置来模拟，每次扫描的耗时是O(t)，所以总时间 t*O(t) = O(t^2)

与NTM和DTM的关系：正交

✅3.SAT问题，逻辑公式可满足性（作业）

考试题估计很接近这种

assignment是一种赋值，由赋予变量的真值组成，literal是带符号的变量，二者的取值都依赖于变量本身的赋值（也就是assignment）

⚠️注意上面第二问（b），证明规约，那么正向和反向都要证明成立，也即也要证明!=SAT车成立可以使得3SAT成立；而证明c，要先说明b的规约方法是多项式规约

NP: give an algorithm for NTM: 先解决一个SAT问题，然后将原来的式子析取上一个子句（这个子句要否定原来找到的那个赋值，比如原来a=1，b=1的赋值可行，那么就析取上一个（-a合取-b的子句））然后对新的formula再求一个SAT问题即可。没那么复杂！

algorithm：随机给出两组赋值A1，A2；先验证A1！=A2，然后再分别验证是否赋值就行。NP基本上都是要

**NP-hard:**规约，增加一个变量以及对应的子句得到\phi1=（x V -x）合取 \phi，如果SAT的表达式\phi有解，那么\phi1有解（在\phi的assignment的基础上加上x为0或1）反过来也是如此；

**规约时间分析：**遍历已有的所有变量，从而找到一个没用过的变量（如果之前用过，那么不能保证x取反的时候，原来的x所在子句依然为true），因此时间是O(n)级别的

证明SAT∈NP-hard

对于一个语言A∈NP，我们构造他的NTM的配置图（起始是输入状态，中间是过程，最终必须是accept）

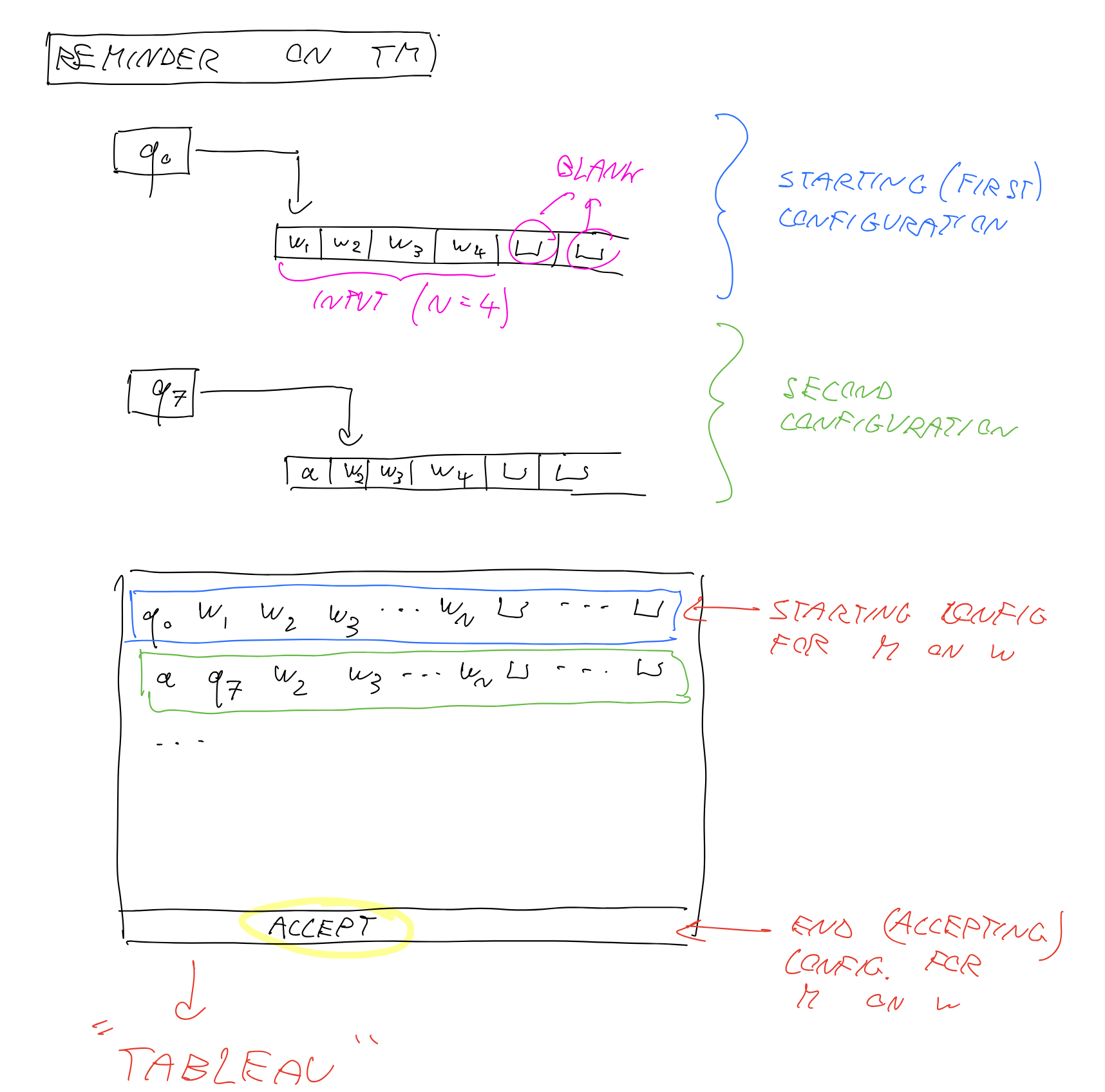
**构造布尔公式：**起始，终止，单元格，转移

3SAT规约到clique

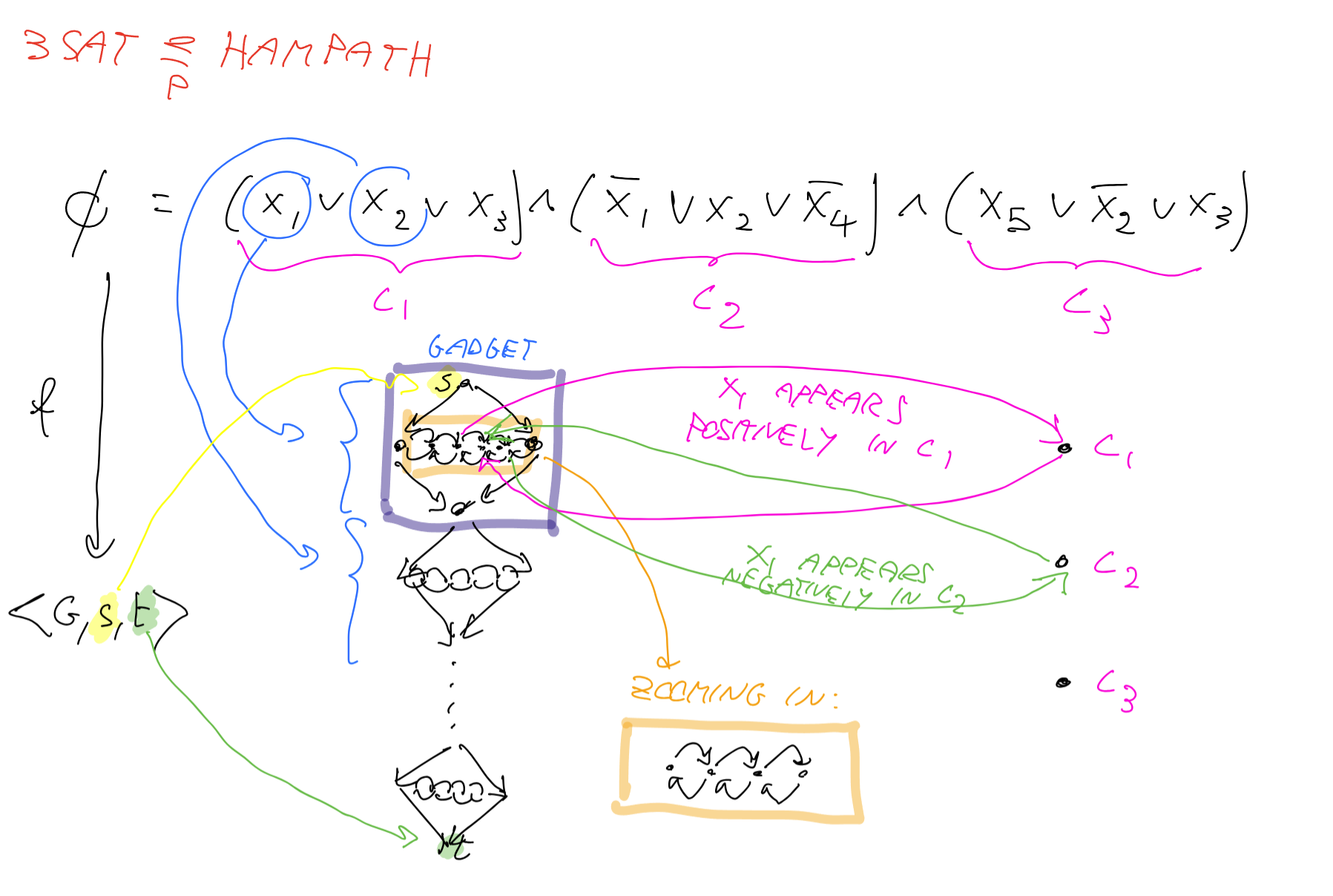
3SAT规约到Hampath

• 每个子句额外多加一个节点c_i
• 每个变量多加一个菱形结构（上节点，中间层和下结点）：中间层的遍历放向对应变量的赋值（如果从左向右遍历，那么对应true，反之对应false）
• 如果一个变量在子句中文字为真，那么就从一个节点连线到c，再从c连回这个节点的右边的下一个节点。

规约的等价性：如果存在赋值，那么就存在一条遍历的路径，能够访问所有的节点一次且仅一次

✅4.NP类问题的证明方法

给出一个NTM的算法

定义证书

如果存在一个结果（证书），那么就猜出来这个结果，并且能在poly时间内验证（给出NTM的操作算法，并进行时间复杂度分析）

SAT∈NP

！✅代入赋值并计算公式真值是一个"简单（Easy）"的过程，可以在多项式时间内完成。

证书：一组赋值

验证：代入这组赋值，验证器检查在该赋值下，公式中的每个子句是否至少有一个文字为真。

效率分析：

• 证书长度：对于 n 个变量，证书长度为 n，是输入规模的多项式级别。

• 验证时间 ：代入赋值并计算公式真值是一个"简单（Easy）"的过程，可以在多项式时间内完成。

✅5.PSPACE类的证明思路

一般

给出一个NTM/DTM的算法，这个算法可以穷举，消耗很多时间；只是不能存下所有，消耗超过多项式级别的空间

• 对于叶子节点，xx
• 对于非叶节点，xx

spacial analysis：apply space-reuse rules，最多只需要存储xx，是多项式空间的

**特别：**规约到已知NP的语言上

oh4的第一题

✅6.二分图（定义+充要条件）（office4中例题）

对于一个连通图connected graph：

重要方法：从某个节点开始进行2-color着色

• 是二分图：等价于着色后，没有任何一条边的两个端点是同颜色的
• 不是二分图：等价于存在一个边，其两个端点是同颜色的

是二分图也等价于不存在奇数环

拓展：二分图规约到2SAT：

抓住二分图等价于可二着色 ，也就是2color着色后，同一条边的两个端点颜色不同，所以只需要对每一个节点生成一个变量，例如a/b，每一条边对应a异或b就可以了，而a异或b又可以等价为两个子句的合取：(a V b)合取 - (a 合取 b)，即(a V b)合取(-a V -b)

✅ 7.（难点）NL-complete问题的分析证明

lecture10中介绍了证明PATH属于NL-complete的方法【回放的45:45】

证明PATH是NL-complete

**证明是NL：**给出一个NTM的算法

✅：只存储当前节点的索引，和走过的步数

证明 PATH 问题∈NL ：先给出一个证书：s 到 t 的一条路径，然后我们可以在对数空间内内验证这个路径：存储当前节点索引和步数计数器（上限为 n），其消耗空间是对数级别的，

NTM算法：【这个算法不对，这个算法要poly空间了，是PSPACE证明才用的】

• 从起始节点出发
• 如果当前节点是目标节点，停机，accept
• 否则，如果节点有未探索过的后继结点，继续探索
• 否则，返回上一节点
• 如果结束遍历，还没有accept，那么就reject

spcial analysis：apply spacial-reuse-rule, 最多同时存储一条路径的节点，每个节点存储对应节点的索引

**证明NL-hard：**证明一个NL问题可以规约到PATH问题

一个NL问题A，求解这个问题的NTM是M，因为A∈NL，所以M使用的空间空间是log-SPACE（也就是说他的一个配置是log-SPACE级别的）

构造过程（规约使用空间的分析）：对每个配置赋予一个节点，遍历每一个配置对，如果这是一个合法的转换，那么就输出对应的两个节点之间的一条边；由于工作纸带只处理配置对，而配置是log-SPACE级别，所以规约过程是对数空间规约

于是构造了这样的图：每个节点存储M的一个配置，如果起点和终点这两个节点之间有合法路径，等价于A为真。

悟!证明2SAT补是NL-complete

证明∈NL： a析取b等价于-a->b和-b->a，每个变量对应一个节点，所以就转换成了节点之间边的关系，2SAT补有解，也就是原来的2SAT无解，等价于存在一个变量x，同时存在节点x到-x的路径以及-x到x的路径，所以2SAT补就规约到了PATH问题，而PATH∈NL，所以2SAT补是NL

**证明∈NL-hard：**从PATH对数空间规约到co2SAT

PATH的图中，每个节点赋予一个变量，每一条边对应一个蕴含关系，一个蕴含关系自然能够转化成一个二元析取式。

**目标：**s到t有路径 <=> 2SAT无解

需要增加额外的约束：

• 对PATH中的s节点，加入子句（xs V- xs），意味着s为true
• 对PATH中的t节点，加入约束t -> -s，也就是加入子句**（-t V -s）**

**悟：**一般从PATH（从s到t有路径）规约到一个新的语言，一把都是要选出唯一的s和t，并赋予他们独特的约束或构造

验证:悟!s为true,不存在路径,那么t为false,所以

解释:

---

估计类似这种

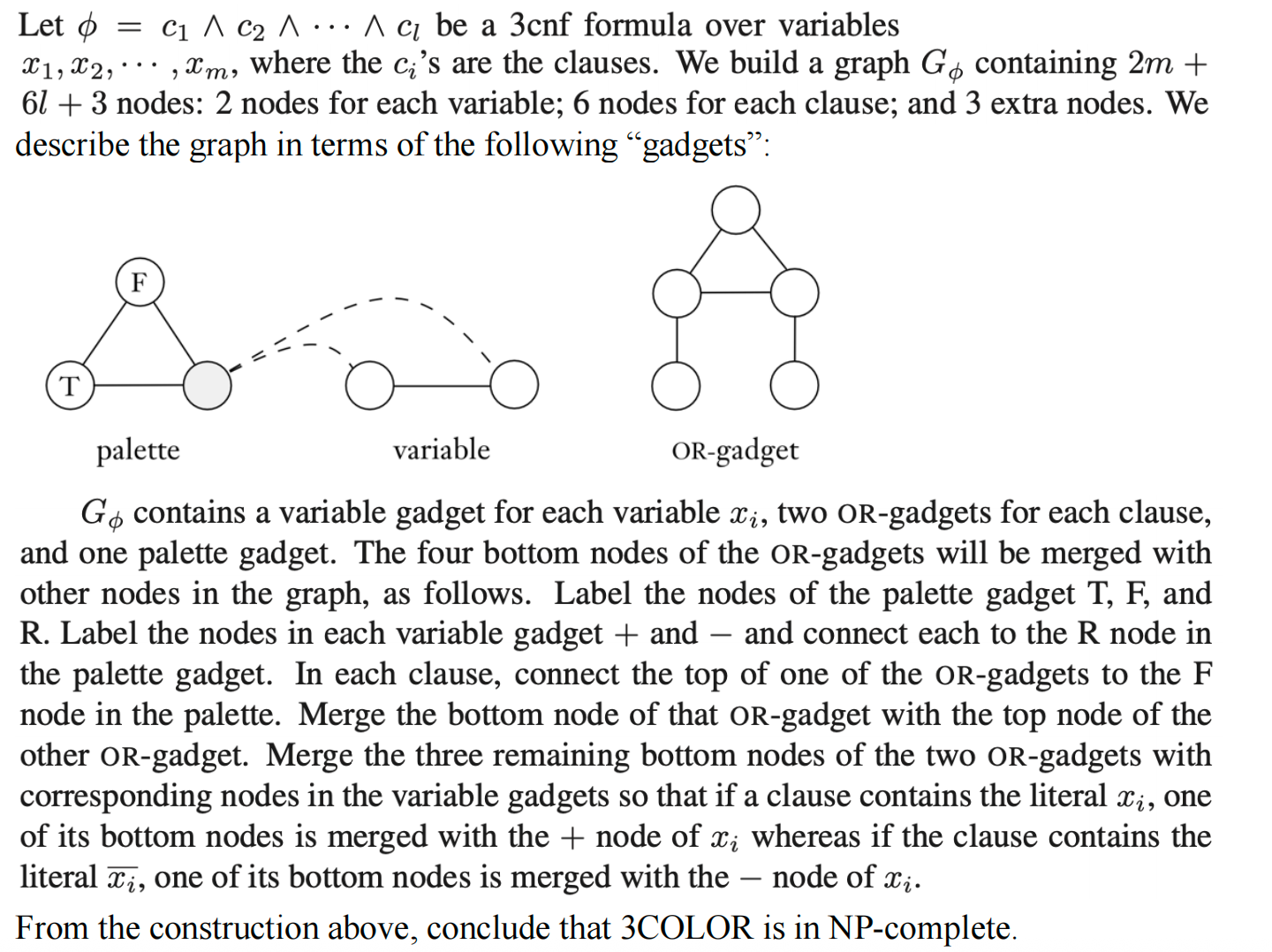
🍑8.NP完备性的性质？（P和NP是否相等）（作业题，如果二者相等，那么有xx？）

✅P=NP的重要推论：NP对补集closed！因为这时coNP=coP（所以有coNP=coP=P=NP）

• 
• 

第一问

• P=NP可以推出NP对补集closed，那么问题从证明"是最短的"变成了证明"不是最短的"，所以假设存在一个更短的，那么我就能用NTM非确定性地给出这个更短的公式并验证
• **通过异或转换成NP问题【语句相等等价于做异或为0（无解）】：**我们有一个verifier（一个更短的布尔公式，我们假设是a），假设原来的式子是b，那么我们需要验证（a异或b）是非SAT问题，这个问题是coNP问题，由于NP=P，所以coP问题也是P问题，即可以在多项式内求解（验证）

第二问

其实暴力枚举所有情况就可以，只是每次枚举所消耗的空间是多项式级别的就行

输入是一个长为n的公式 l，构造一个同样长为n-1的字符串s，其中的每一位既可以是l中的某个变量，也可以是一个运算符号（析取/合取）

NTM算法：

• 非确定性地构造一个字串s
• 首先判断这个构造的字串是否合法，以及是包含l的所有变量，如果不是，直接舍去这个s
• 接着，验证s和l是否等价（遍历所有的赋值情况，这里的时间开销可能较大，但是消耗的空间始终是m个变量赋值所占用的空间m），如果等价，那么就reject
• 如果遍历了所有的s，都没有reject，那么就accept

spacial analysis：显然，这样的字串有n的指数级个，但是每次只需要存储当前的s，长度为n-1，所以是多项式空间的

误区：

1. 更短的不一定是长度少1的，可能是长度少很多的【离散的长度跳跃：布尔公式的等价变换往往不是"连续"的。通过逻辑代数规则（如吸收律、分配律），一个复杂的公式可能直接简化为一个极简的公式，中间可能不存在任何"过渡长度"的等价形式。】
2. 仔细审题：题目是要在"same set of assignments"，是所有的赋值下都要成立

❌对每个literal，删除，然后验证相应的子句是不是在原来的赋值下仍然true，如果是，那么说明不是最短的，如果每个literal都尝试过了，那么就是最短的，整个验证过程只是验证子句是否为true，可以在poly时间内完成。所以是NP。

✅证明min-formula是NP：如果存在更短的公式，那么我们可以在多项式时间内验证这个结果，非确定性地选择一个赋值，然后验证两个公式是否等价，这个时间消耗是poly-time的，所以是NP问题

枚举所有have the same set of variables and 长度比原公式段的formula，verify whether they are true on the same set of assignments.

对PSPACE问题，一般是要给出一个递归算法，(如果是叶子节点那么xx，如果是中间那节点xx，什么时候停机）；采用SPACIAL-reuse-rules；spacial analysis：节点*最大递归深度+节点之外存的

2. 空间复用规则，对每个子句进行分析，删除一个文字，然后判断是否为true

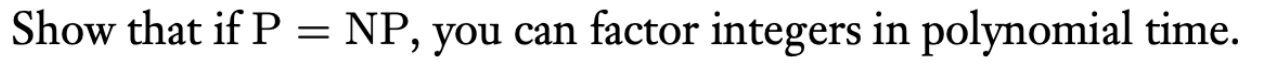
不熟！悟！

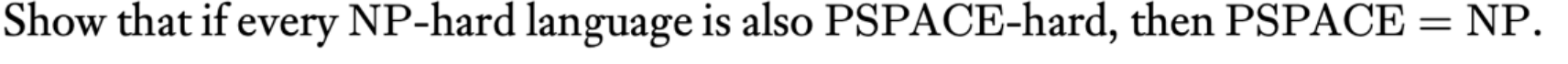
证明相等，一般就是要正/反地证明规约关系，关键是要证明PSPACE包含于NP

重要性质：NP对多项式规约closed，所以只要能多项式规约到NP问题，那么就是NP问题

关键是，PSPACE可以规约到PSPACE-hard，现在根据题目设定PSPACE可以规约到NP-hard，找一个NP-complete 中的类SAT（他也是NP类中的），所有PSPACE可以规约到SAT，加上NP对多项式规约closed，所以PSPACE都是NP。【用complete联系X和X-hard】

✅9.Savitch定理

Savitch定理

定理本身的证明逻辑：

基本定义

✅也就是说，NPSPACE中的语言，需要NSPCAE（f（n））空间来求解，根据savitch定理，也就是需要DSPCAE（f（n）^2）空间来求解。

关键推论：PSPACE = NPSPACE

因为多项式的平方，依然是多项式。具体证明如下：

相关概念

区别NSPACE和NPSPACE，前者是空间描述，后者是问题类

⚠️ 10.coNP问题的定义与扩展

//建议去看课件

**复习作业关注：**NL-complete，P=NP的设定，coNP，空间与时间关系等

典型"大哥"定义（NX-complete）

NL-complete

PATH (又称 ST-CONN, 有向图可达性) ：特定两点之间的可达性

• 定义 ：给定有向图，是否存在从特定两点之间 s 到 t 的路径。

2-SAT：（SAT的一个子类）

• 注意：虽然 SAT 是 NP-hard，但每个子句只有 2 个文字的 2-SAT 是 NL-complete 的。

NP-complete

SAT / 3-SAT (布尔可满足性问题)：

Hamiltonian Path (哈密顿路径)：

NPSPACE-complete（包括两类游戏）

TQBF

公式游戏（Formula Game）= TQBF

公式游戏与TQBF问题等价

GG

---

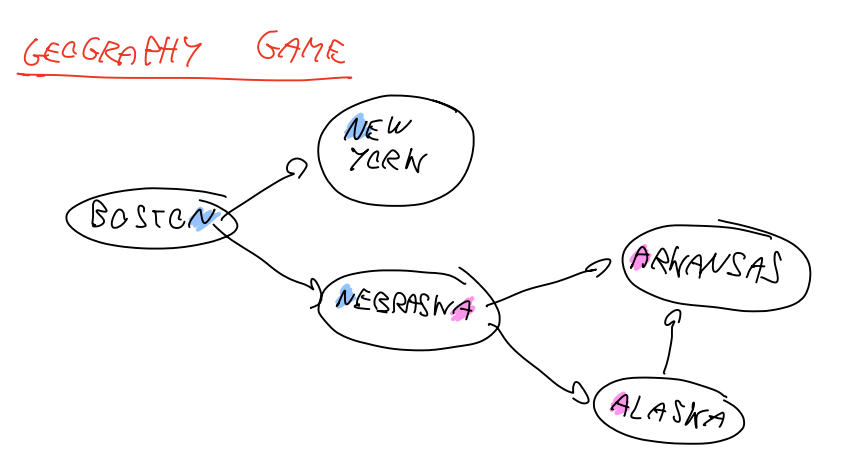
各类别之间的关系

重要认识：

1. X对补集closed就是X = coX（P = coP）
2. L∈P，就是存在一个算法A，能够在多项式时间内判定L

NPSPACE 与 PSPACE 是相等的，即NPSPACE=PSPACE

tip：NP-complete 是NP-hard和NP的交集**，在证明题中可以用来沟通二者。**

这五大类中，只有NP不知道是否对补集closed，其他都是：X和X-complete都是对补集closed！

✅要证明属于X，可以用A规约到已知是X的B的方法

✅但是要证明A属于X-hard的话，那就需要一个已知X-hard的B来规约到A

包含关系

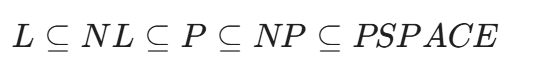
complete的规约关系

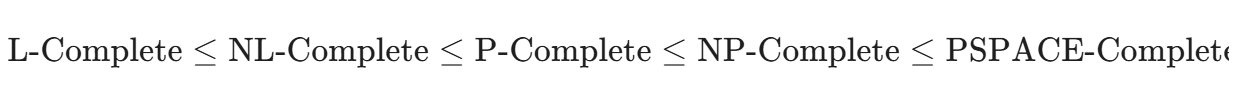
其中L/NL使用多项式空间规约的方法

规约要求双箭头！

对规约closed的类，包括NP！

对数空间规约：所有

poly时间规约：P右边

X-complete，X-hard和X

【X-complete都是X-hard和X的交集】

【如果 X 中的每一个 问题都能在多项式时间内规约到问题 H，那么问题 H 就是 X-hard。】

注意 ：X-hard 不一定在 X 里面！ 它可以在 X 外面，甚至难到不可解。

L和NL【详见Gemini对话】

L 和 NL 都是很"弱"的类（它们包含于 P）

NL就是认为如果存在一个解，那么我们就可以直接找到这个解，于是空间消耗就是这一次查找的消耗

单词积累

运算符号 operator

异或 XOR

• 并运算 (Union)：两个多项式时间可解问题的"或"组合仍然可以被高效解决。

• 连接运算 (Concatenation)：将字符串拆分为两部分并分别验证，由于拆分方式有限（线性个），总时间仍为多项式。

• 补运算 (Complement)：只需将判定机器的"接受"和"拒绝"状态对调即可。

更新 update

模拟 simulate

遍历 traverse

递归 recursion

虚拟读写头 virtual read/write head

单元格 cell

转移函数 transfer function

有限状态控制器 finite controller

遍历每一个配置对 iterate each configurationpair

分治算法 divide and conquer algorithm

proof for xx

suppose xx，Let n = xx

algorithm：算法：

• interation：迭代/循环 //后面写算法，ifxx，accept/reject
• termination：终止 //后面写停机条件

Time/spacial complexity analysis：polynomial bound

PS：exponential 指数级

conclusion:

clique：小圈子，团

3-clique：有三个顶点的小团

triangle：三角形

cnf：合取范式【子句之间用合取连接】

3cnf: 三维合取范式【每个子句各有三个变量，变量之间用析取连接】

3SAT：判断一个3cnf是否有解（赋值方法使整个句子为True）

literal:文字，即一个变量或者它的非

clause：子句

negation:否定，取反

assignment：赋值，即对公式中所有变量分配具体的值（T or F）

✅literal 是带符号的 variable ；就比如 A 和非 A 是同样的 variable，但是是不同的 literal 是吗，是~

证明

证明一个问题 A 是 X-Complete（比如 NP-Complete），你永远只需要做两步"广播体操"：

1. 证明 A 属于 X (Membership)：确立上限（它没那么难，属于这个圈子。【按照定义：NP是"假设猜出结果，能够在poly时间内验证"； P和PSPACE是写出一个TM的算法，说明能够在poly时间/空间内解决】

2. 证明 A 是 X-Hard (Hardness)：确立下限（它很难，所有 X 问题都能规约给它）。【一般就是选一个已知的X-hard问题，找到一个变换f，使得这个问题能够多项式时间内规约到A】【X-hard语言能够在多项式时间内规约到A，就说明A是X-hard语言】

​

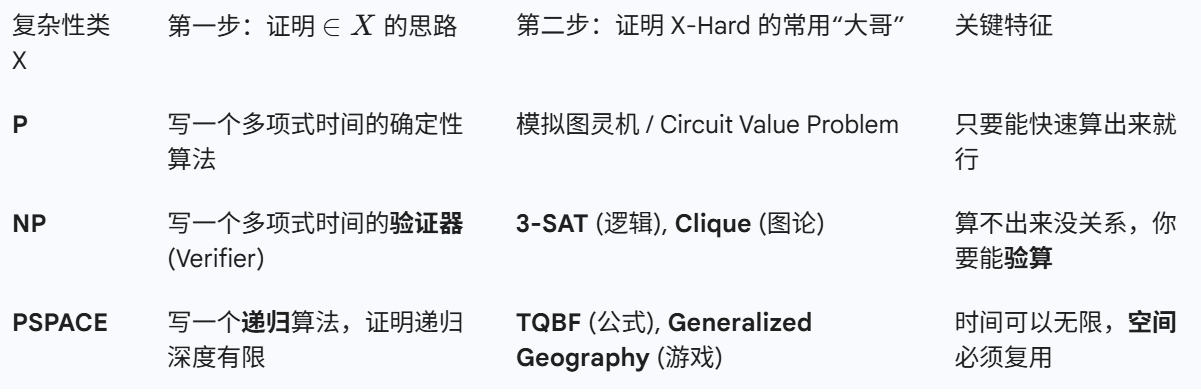
证明NL-complete

典型例题

证明是NL

方法：证明补集是NL的

【✅对数空间规约】证明NL-hard

多项式空间规约：区别"输入方/接收方"和**"转换器（中间使用）"**

多项式空间规约，要求的是这个转换器使用的空间是多项式空间的（比如维护几个指针/索引/数值等），而不关心输入输出的空间需求

​

证明 NP**-Complete**

步骤一：证明 A \\in NP

• 核心思路 ："猜+验证" (Certificate & Verifier)。

• 怎么做：不要试图去解这个问题（解太慢了）。

  • 告诉老师："如果我凭空猜一个答案（Certificate），能不能在多项式时间内检查这个答案是对的？"

步骤二：证明 A 是 NP-Hard

• 核心思路 ：从 3-SAT （万物起源）或 Clique 等已知 NPC 问题出发。

• 怎么做：构造一个函数 f，把 3-SAT 的公式转化成你的问题实例。

证明 P**-Complete**

步骤一：证明 A \\in P（TM可以在多项式时间内求解）

• 核心思路 ："直接算"。

• 怎么做 ：直接写出一个确定性算法，证明它能在 O(n\^k) 时间内跑完。

步骤二：证明 A 是 P-Hard

• 核心思路 ："模拟图灵机"。

• 怎么做：通常需要证明你的问题 A 能够模拟任何多项式时间图灵机的运行过程。

• 例子：

  • 选大哥：任意 P 问题。

  • 规约：我们要证明任何 P 问题都能在多项式时间内转化成 A。

证明 PSPACE-Complete。

证明问题 A 是 PSPACE-Complete。

步骤一：证明 A \\in PSPACE

• 核心思路 ："递归与复用"。

• 怎么做 ：证明你可以写出一个算法 ，虽然它可能跑得慢（指数时间），但它占用的内存深度必须只有多项式级别。

• 例子 (TQBF - 真量词布尔公式)：

​

步骤二：证明 A 是 PSPACE-Hard

• 核心思路 ：规约自 TQBF 或 Geography (接龙游戏)。

• 怎么做：PSPACE-complete 问题通常都带有"博弈"或"全称量词"性质。

• 例子 (证明 Go 围棋残局是 PSPACE-hard)：

  • 选大哥 ：Generalized Geography (图上的接龙游戏)。

  • 规约：试图把图上的节点移动，映射成围棋棋盘上的落子。

  • 论证：如果你能算出围棋必胜策略，你就能算出 Geography 的必胜策略。