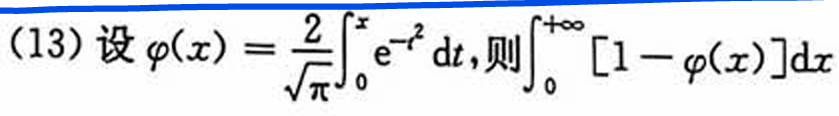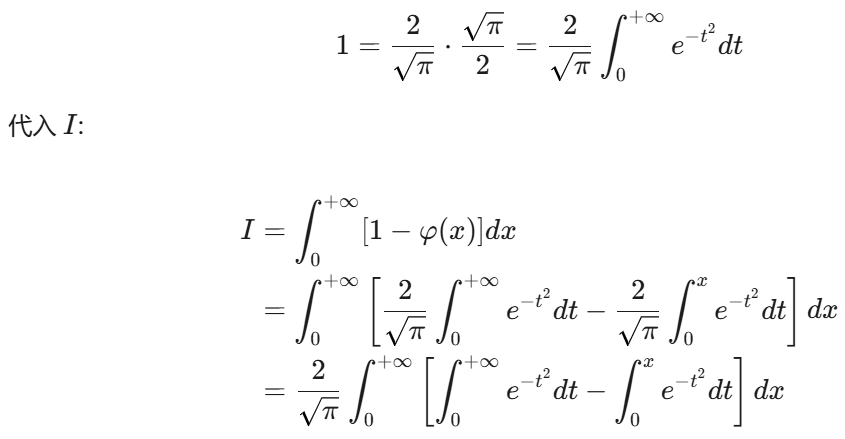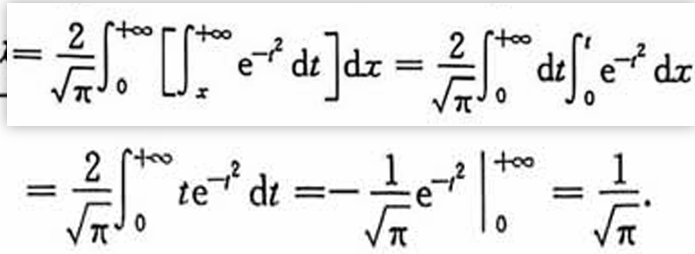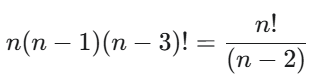多元微分
概念
偏导数表示形式2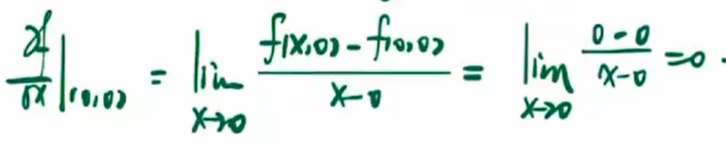




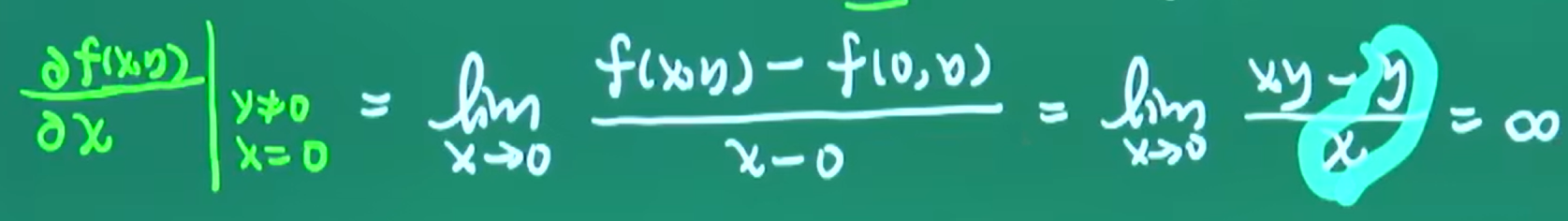
y当为常数处理,不是趋近于0。


常数函数在任何点都可微,特别是在 (0,0) 处也可微。

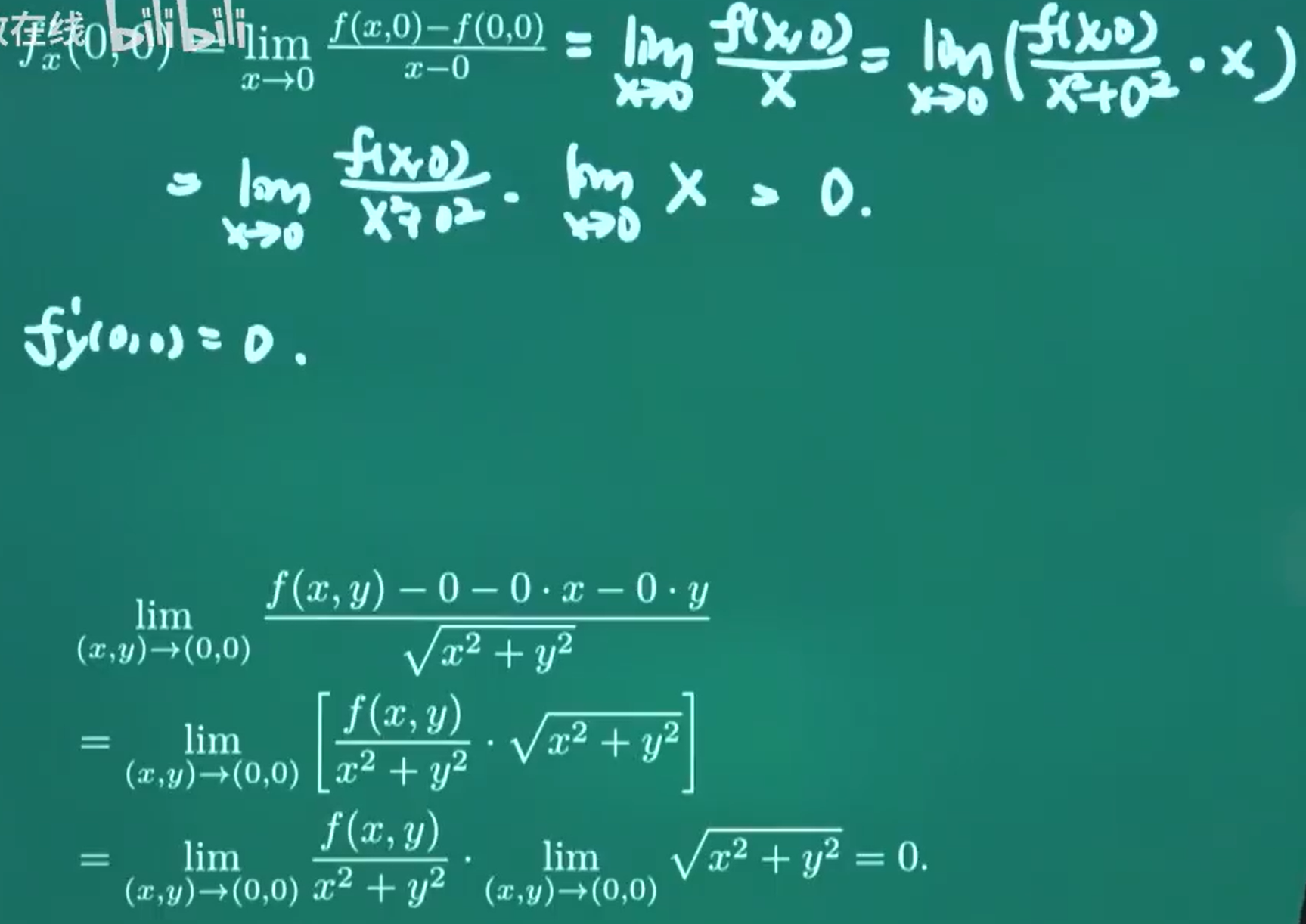
gehttps://www.bilibili.com/video/BV1Ut411p7k3?spm_id_from=333.788.videopod.episodes&vd_source=57591a306a32819eb0018018acdc4ccc&p=13

3、4证明:



1、2证明:


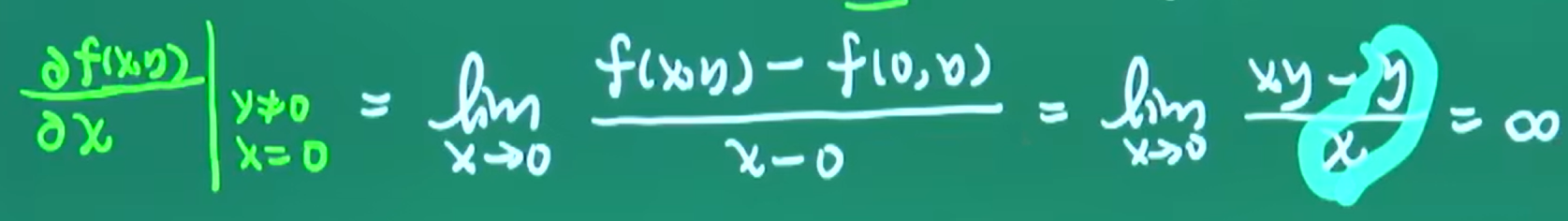
y当为常数处理,不是趋近于0。

偏导数
如果一个二元函数的混合二阶偏导数是连续的,那么混合偏导数与求导次序无关,即:
f''_{ij} = f''_{ji}
混淆了常数求导和函数求导原则:除求导变量外,其余自变量皆视为常数。就是y(x)总有关系,实际不是
原则:除求导变量外,其余自变量皆视为常数。
符号规范: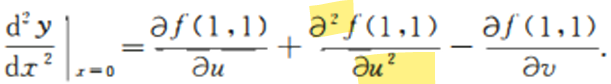

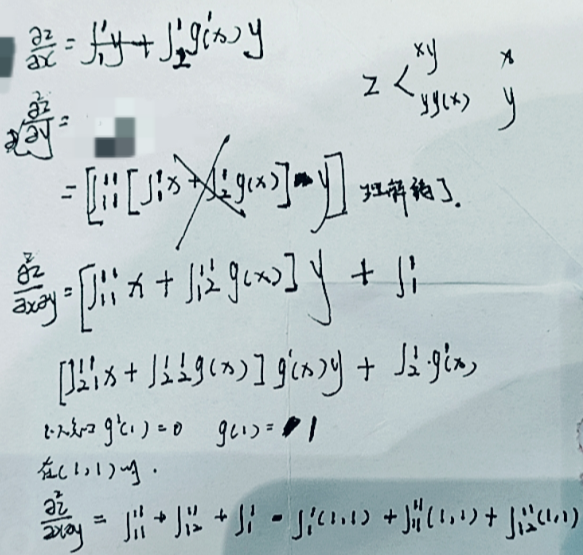
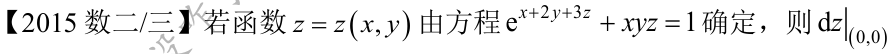



感觉就是这题要分析下,感觉复杂里面嵌套了一个Z。我都是用的隐函数解决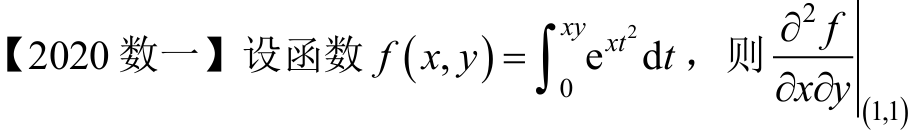


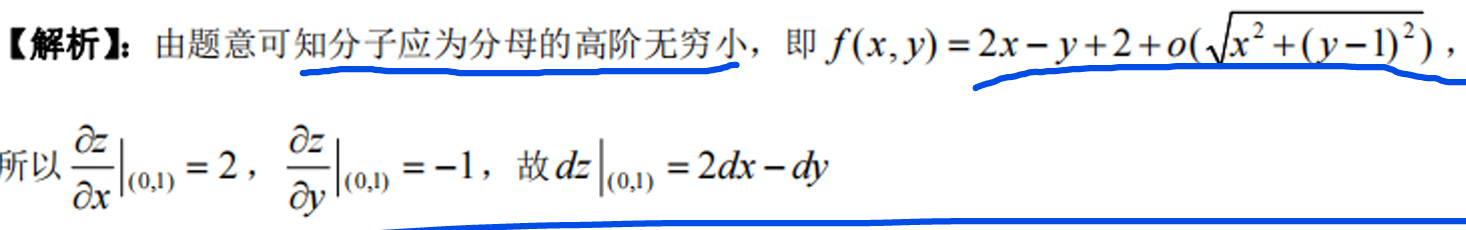

直接求导




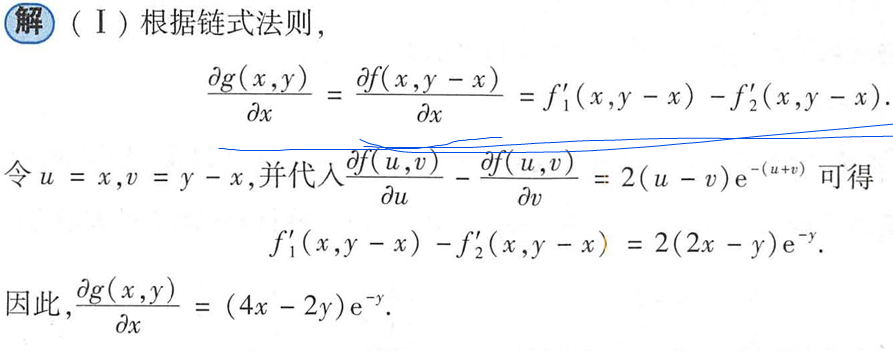



多元极值
无条件多元极值
1.求 f`x f`y 联立求解点
2.求f`xy f`xx f`yy
3.AC-B²
md 忘了AC-B²,不自信第一步联立 为解
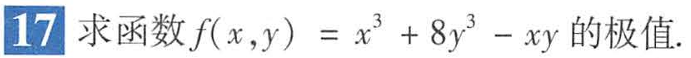
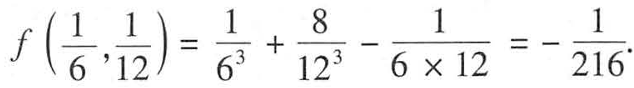

做到这就不会了。连x= 都不知道,认为要联立求。
 if遇到要多元二阶求导不要用隐函数求导,隐函数求导二阶很复杂。
if遇到要多元二阶求导不要用隐函数求导,隐函数求导二阶很复杂。
**何为偏导:**y、x互相独立,太蠢了13章


看错题目了,已知f`x但是未知f`y 。就不可以用那个fy来消∫dy的C。必须求原来的fxy,不可直接求f`y。

算是一个技巧,观察题目f1=0,避免我原本还要计算极小值f0.5。c了


不要忽略边界


全微分形式的不变性


全微分

我想错了,我不是求对应的导,我是求积分

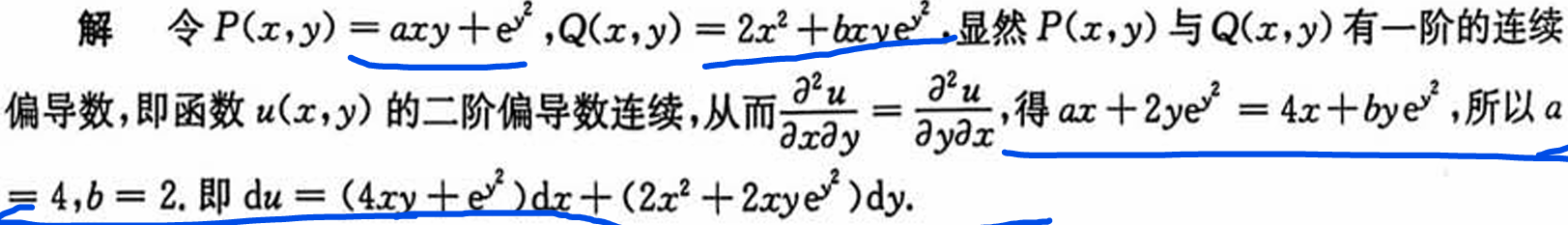


极限
等价无穷小

要使极限存在且不为0,分子的最低次幂必须与分母的最低次幂相同。 



错1,inx 的洛必达我背错了。2、忘记同阶和等价为1。3、直接进行洛必达,得到a=3k这个无用结论;做快了中间这个过程多出来了常数,但是我错误的使用了洛必达,比如这个C1就是a+1,只有a+1=0才可以继续洛必达下去。自然求出来了a==-1.



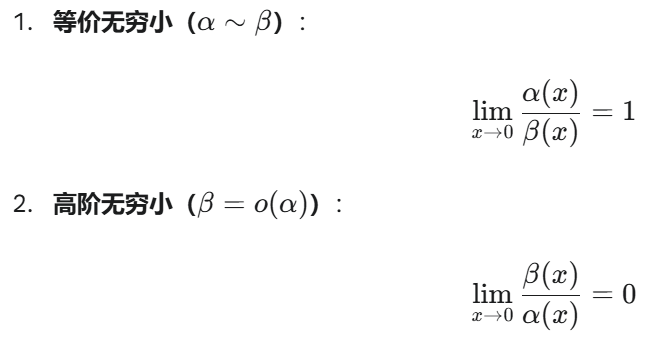





间断点







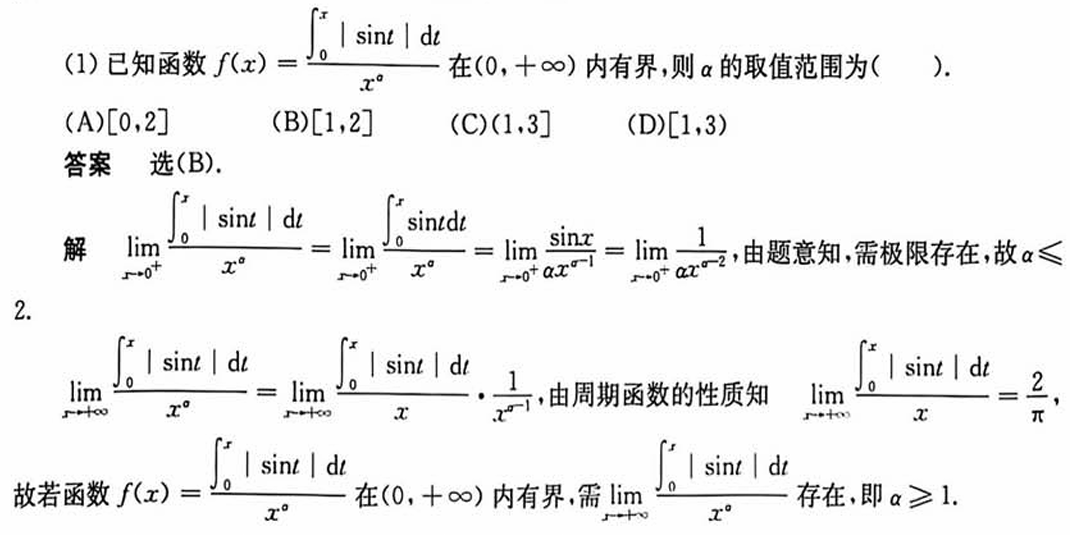
有界
使用性质3:将问题转化为两端极限
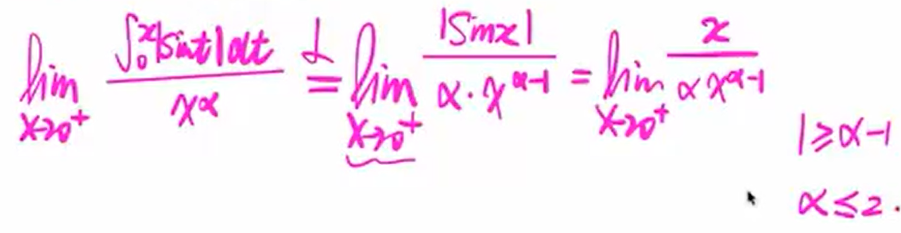

如果分母的x的次方小于1必然整体无穷大。
我如何错的·只考虑了第二种情况,未考虑到0的情况。
渐近线
忘了无定义点:就是if是看+∞,然后到 ∞/x,只用看+了不用考虑-
无定义、分段点、端点------>lim+∞------>lim+∞/x
------>lim-∞------>lim-∞/x


方法2:
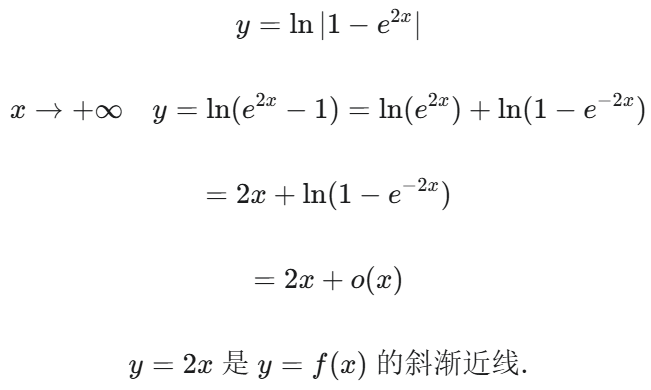
数列极限
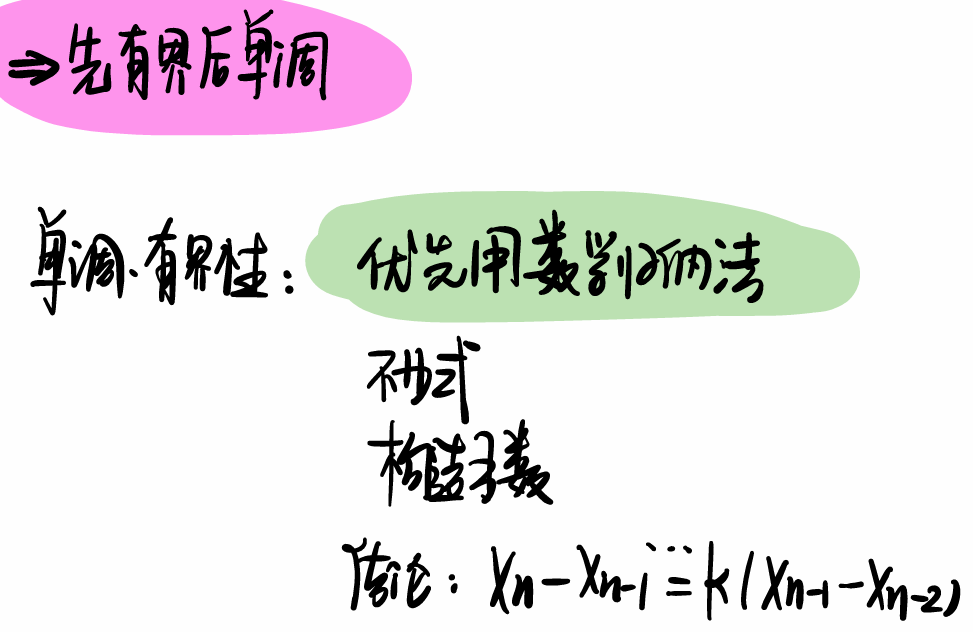

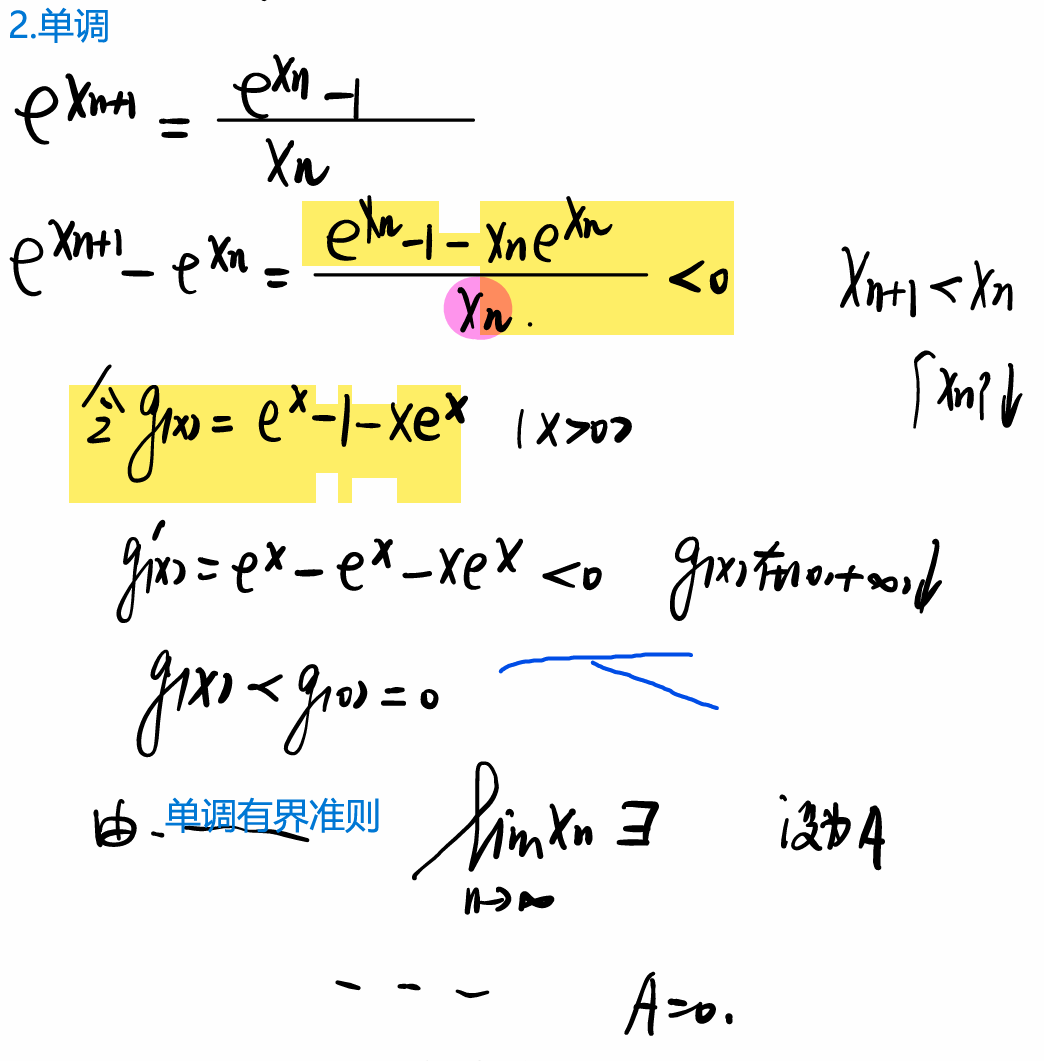

方法之2证明数列{x}单调减少。联想到了上面的拉格朗日极限:

补充练习:
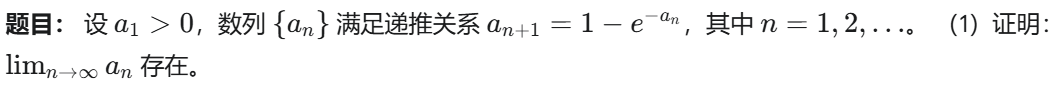


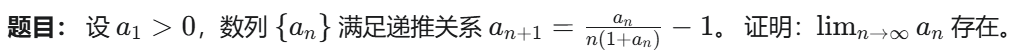





# 拉格朗日极限

对应情况1233


函数连续


极限计算

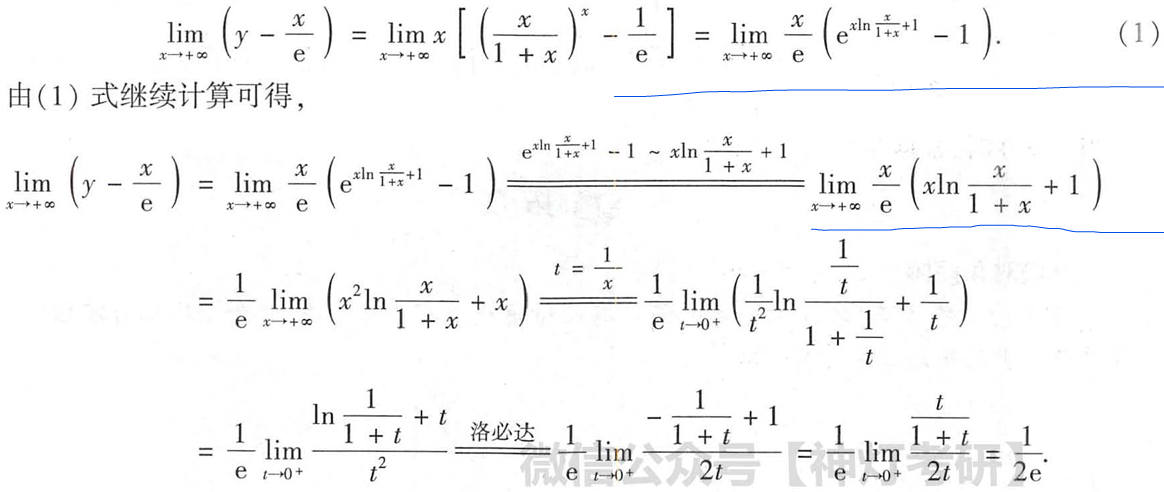
第一步等价是key?

积分
定积分的性质
(1)连续函数f(x)必有原函数F(x)
(2)含有第一类间断点 和无穷间断点 的函数f(x)在包含该间断点的区间内必没有原函数F(x).
++速记:只有震荡可能有,其他一律没有,联想到了f`也是没有第一类间断点。++
就是F(X)可导必连续,但是不能保证F`(X)就是f(X)必然连续,还能震荡,两种情况。

积分周期



第三个
第四个
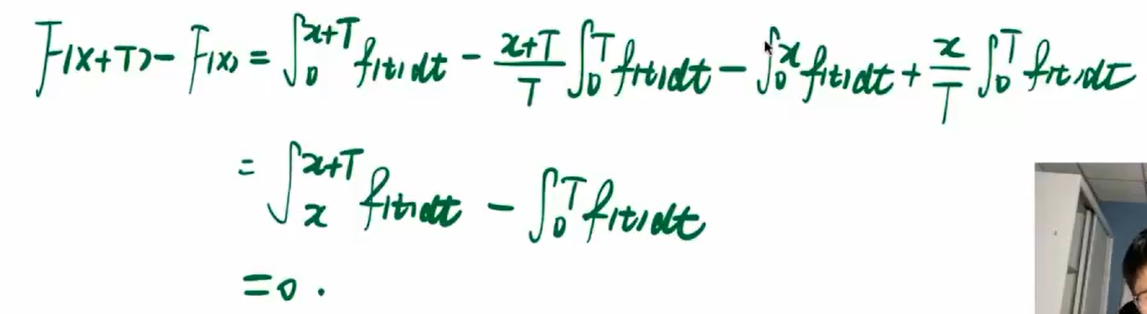
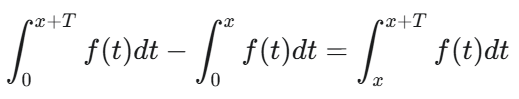
#反常积分的审敛
如果简单可找原函数。
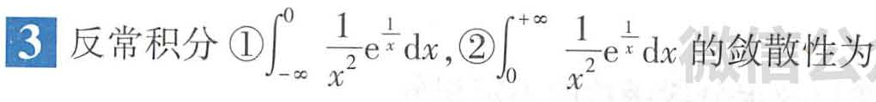





定积分的求和
我以为是夹b

定积分拆分求导型
我是严重混淆了,做的时候是背了当时的一个答案,就是区间相等的时候。

 先检查连续性,如果不连续,则立即结束判断,得出不可导的结论。
先检查连续性,如果不连续,则立即结束判断,得出不可导的结论。

一般来说,可能的极值点包括:
-
给定区间内部的驻点(f'(x)=0 的点)。
-
给定区间内部的不可导点(f'(x) 不存在的点)。
-
区间端点。
-
若函数 f(x) 在无穷区间 上仅有一驻点 ,且该点为极值点 ,则该极值点必为最值点
细节多旋转V

当时想的f1-f2一步到位的算(但是不会曲线方程转换,同时也错了),答案是分开算体积相减法V1-V2。

未能识别为一个球体: 
**让我想到了参数方程算面积,换元的感觉了:**用x=t(t)来换元。

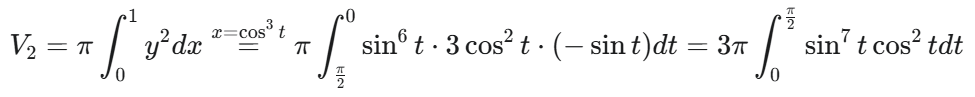
用x=t(t)来换元。
这是另一种处理方法:这是星星线。记住。
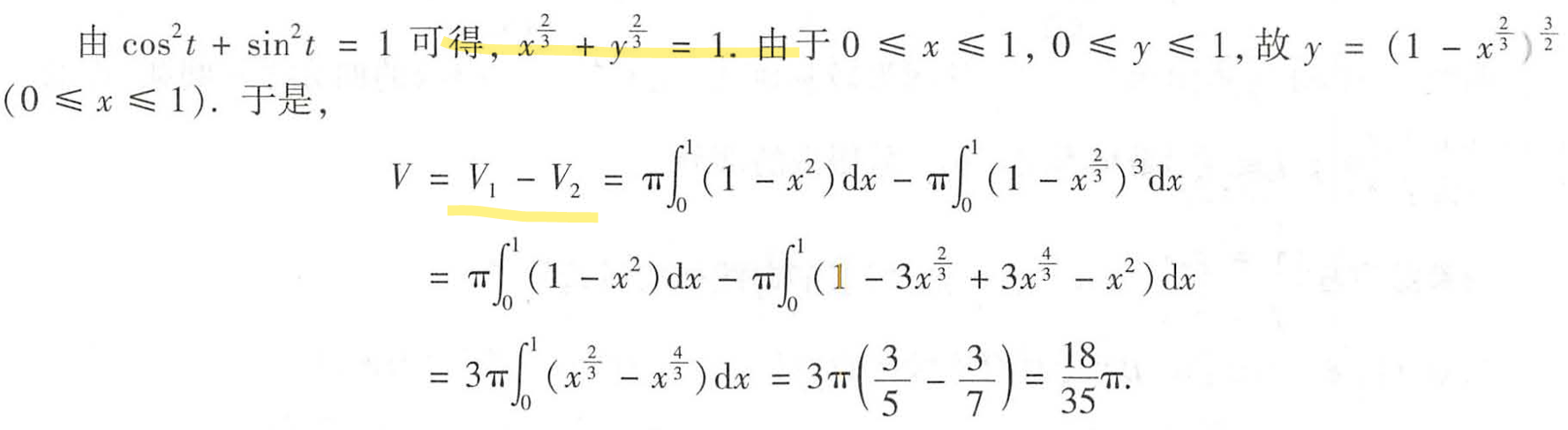
(2)表面积 S1+S2
这里直接ds就是不用什么dx换位dt、ds之类的
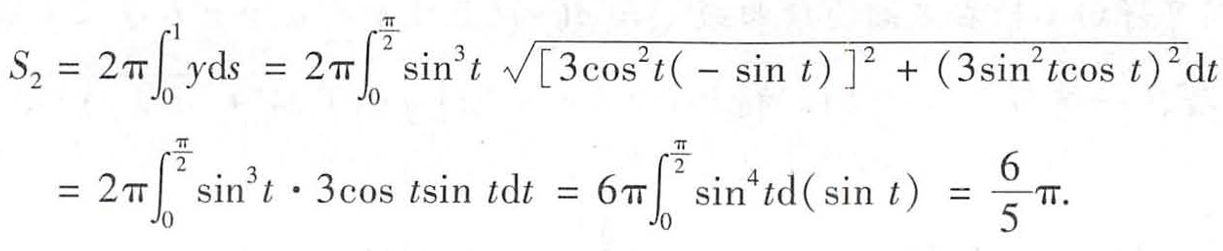

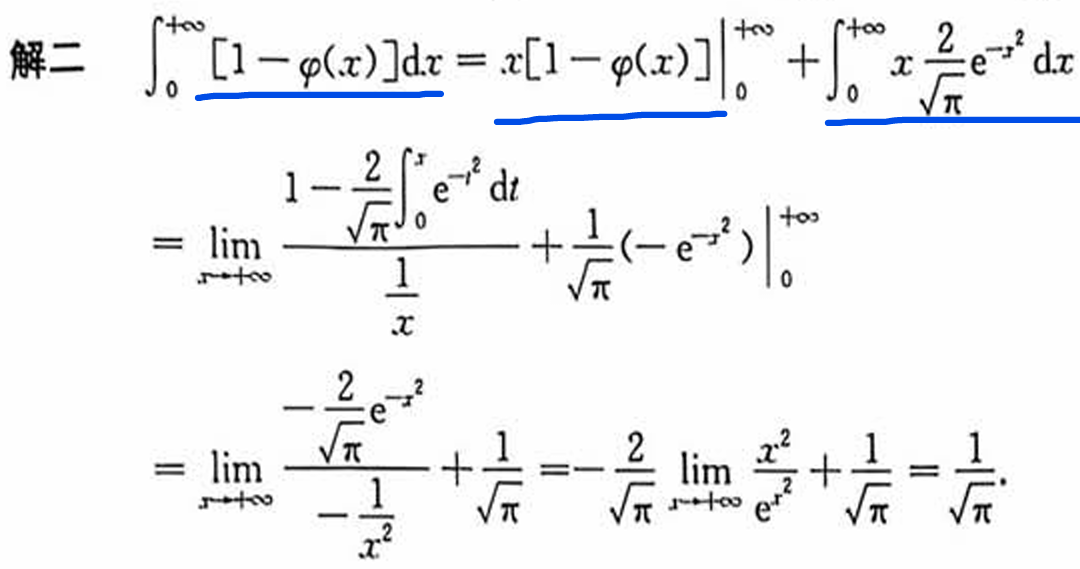
变限积分



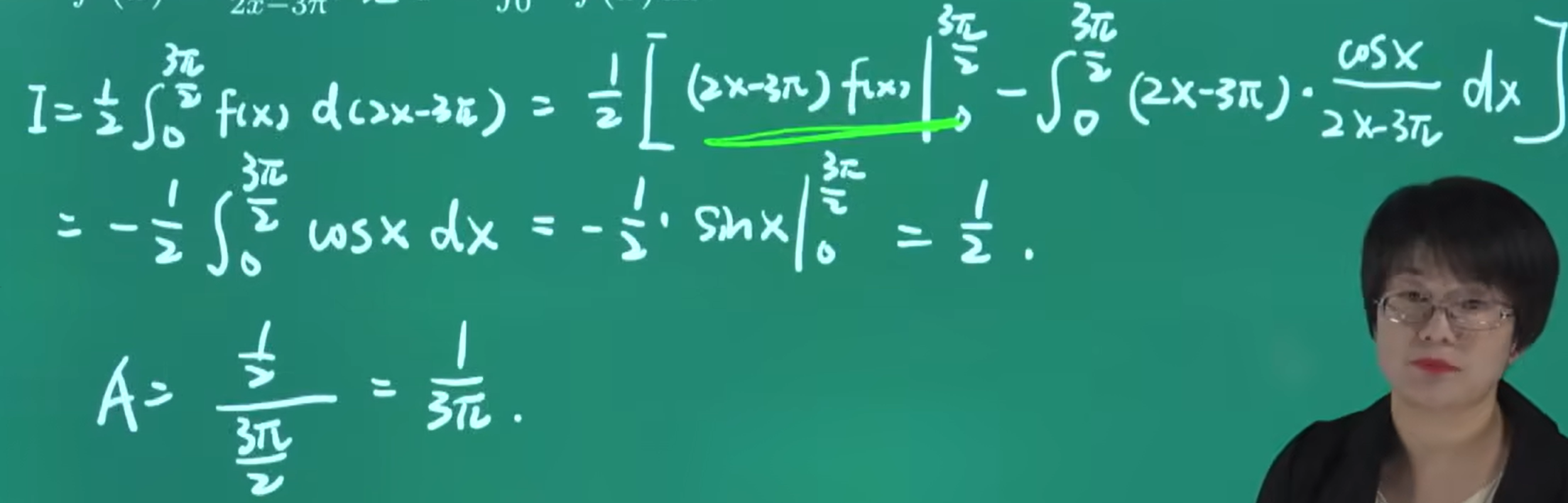
 注第(I)问中的法一使用了分部积分法,比较巧妙.法二用到了交换二次积分的次序.这个想法也是比较自然的,符合我们简化计算的思想.一般地,对一个关于x,的二次积分来说,若被积函数是仅关于t的函数,则先对x积分,再对t积分能使计算简化。
注第(I)问中的法一使用了分部积分法,比较巧妙.法二用到了交换二次积分的次序.这个想法也是比较自然的,符合我们简化计算的思想.一般地,对一个关于x,的二次积分来说,若被积函数是仅关于t的函数,则先对x积分,再对t积分能使计算简化。



#积分比较
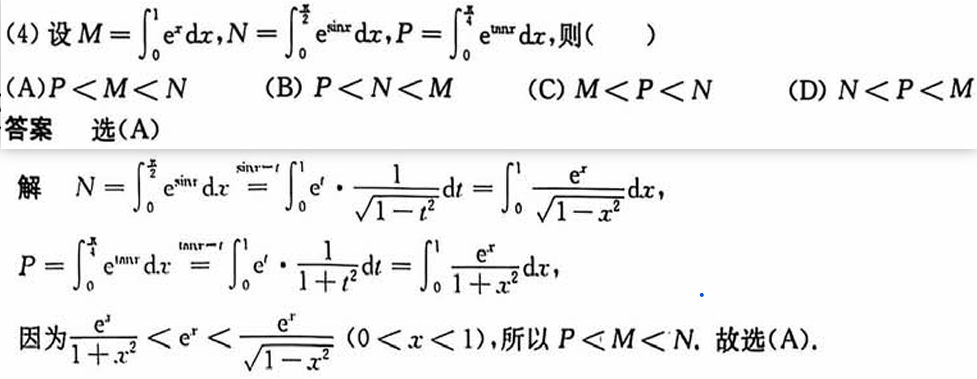
比较方法是化为同一个积分区域。
用1为标准来判断

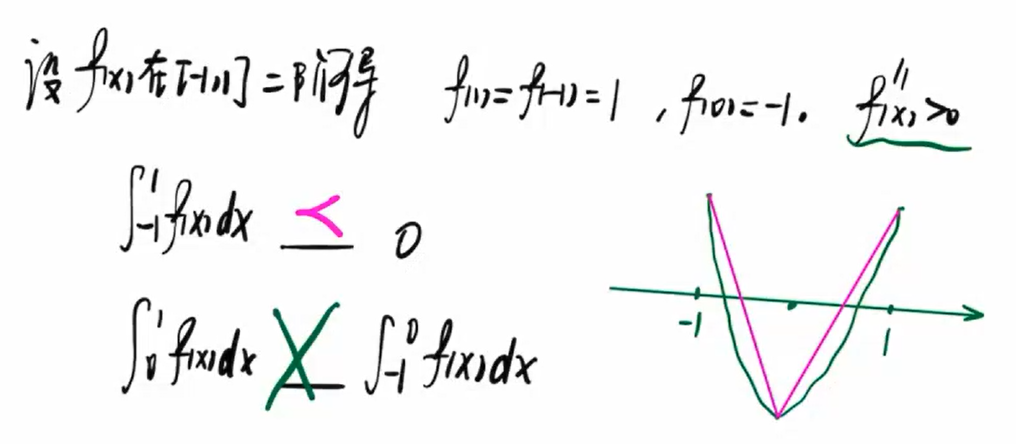




我是把cos等价了与根号下x方y方比较复杂了
积分比阶数


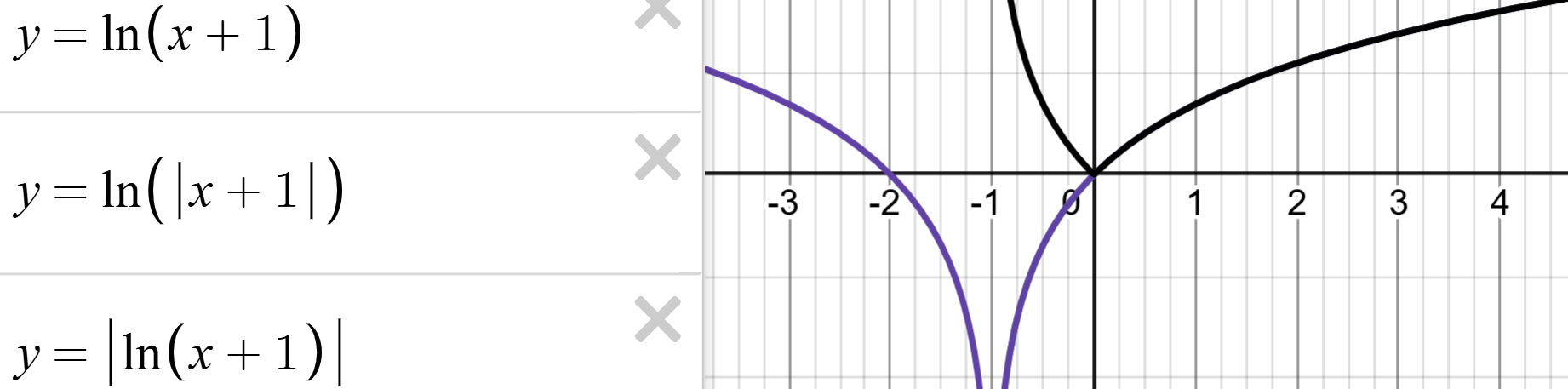
分步积分
计算
18年
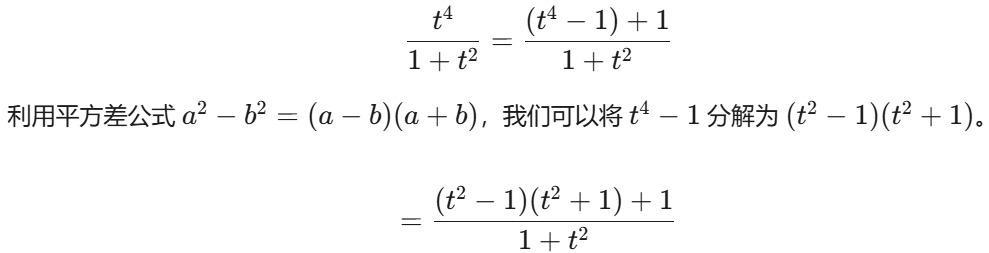
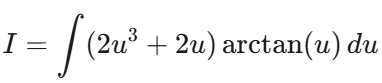 整体分步积分不要拆分
整体分步积分不要拆分 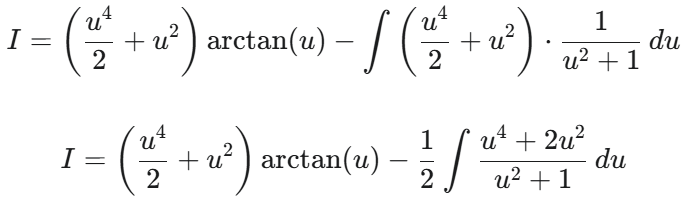
16

求导当作常数了


 两边同时积分
两边同时积分

我换元后直接洛必达死了,分母多化简几次再洛必达就对了




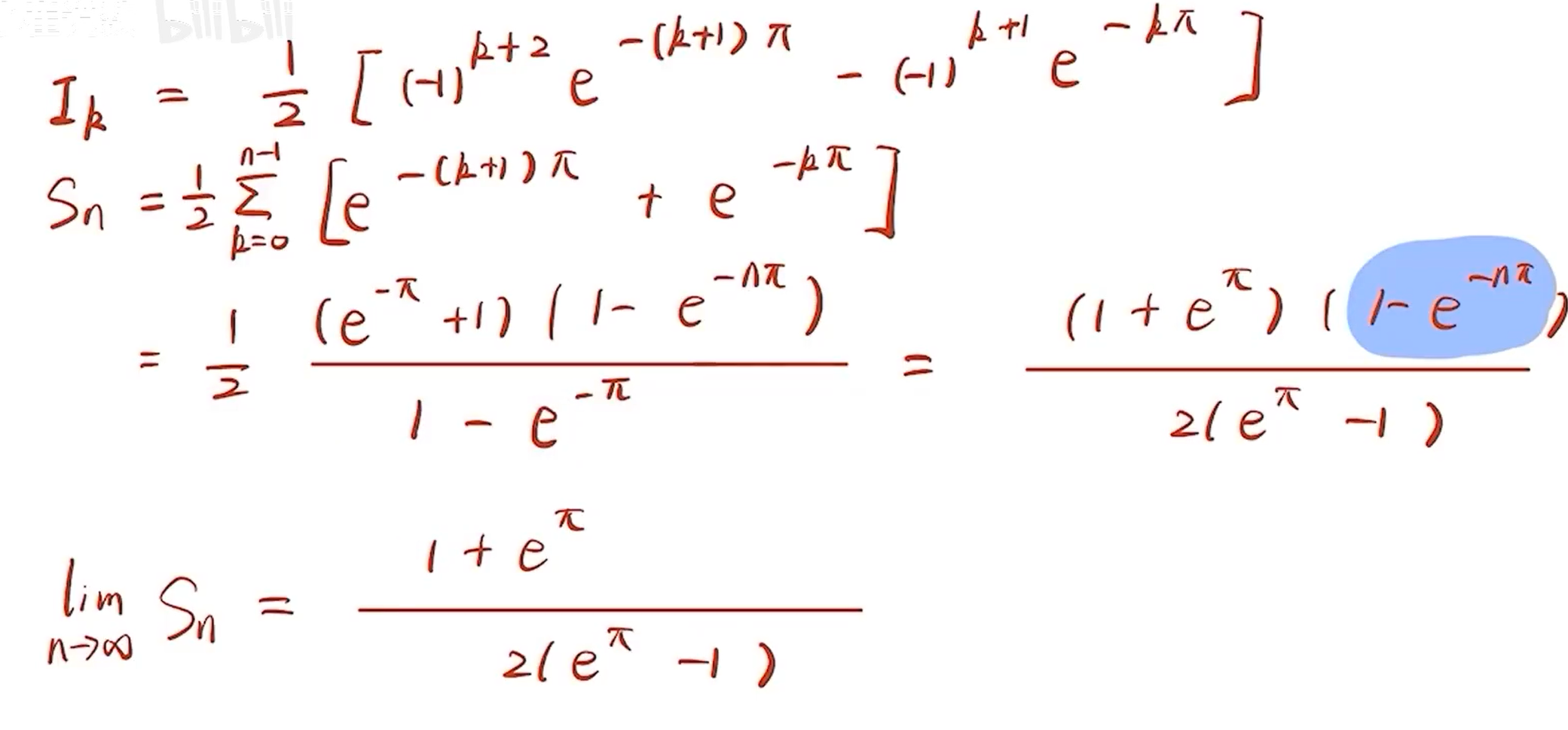
不要区分奇数偶数区间,
物理应用
静水压力


积分面积

导数
概念
未分情况,忽略了题目暗示,根源:未能明显区分导数的连续和存在关系。我只写了导师两边极限相等,说明极限存在,未指出 limfx=fx0。



这个小坑,当时做的时候用了题目条件反而避免了。
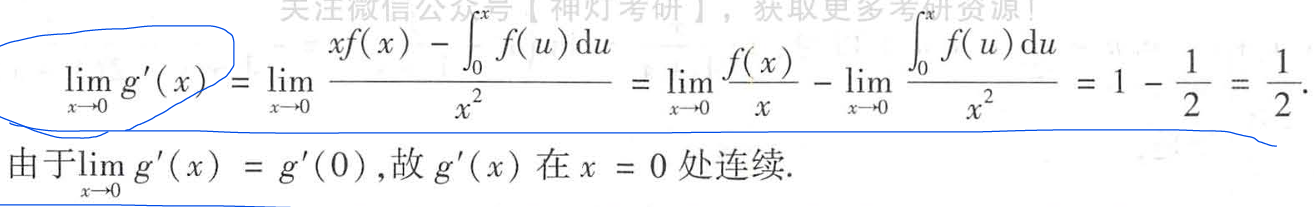




定义

我是如何错的?这个凑得方法没有乘以分母消掉,我直接用x方硬来。
忽略了不可导点,最后的注:是必要的,因为我们默认是一大一小,这个是两小一大。如果是连续便于判断。最好写出表格判断。 

构造函数


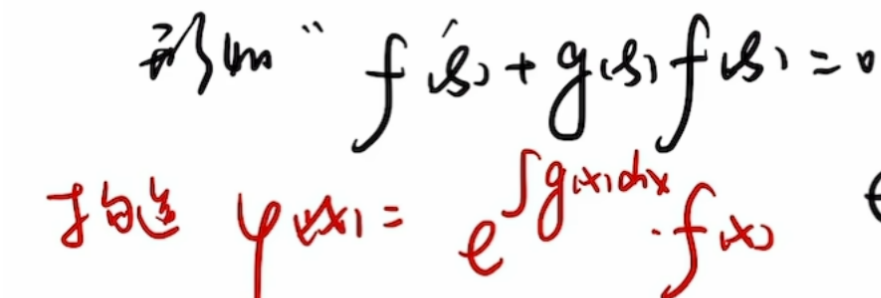

连续*不可导性质

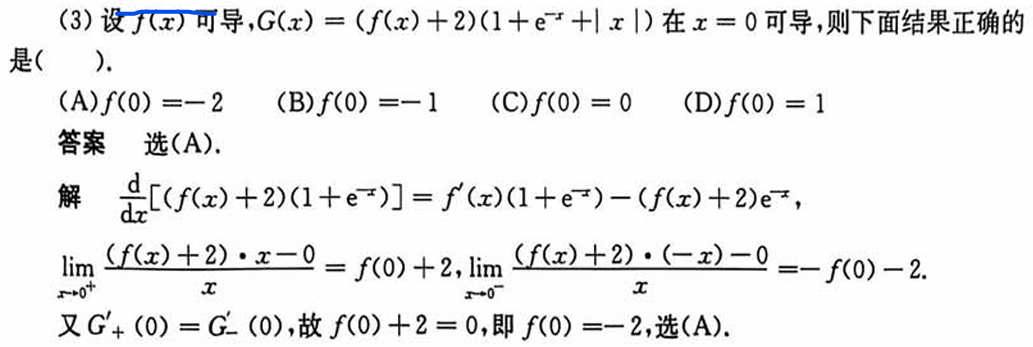
|x|(f(x)+2)这个导数,在这里为0.
曲率
条件未能利用充分f``的含义,当时是找到画图法。






#高阶导数
方法1:莱布,需要归纳法
方法2:泰勒,只用对齐x^n


 所以實際上,這個要調整n=0->2 才可以。爲了便於計算,我們可以用m代替,比如
所以實際上,這個要調整n=0->2 才可以。爲了便於計算,我們可以用m代替,比如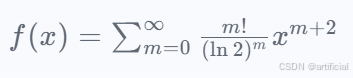 爲了一一對應,x^n自然 m+2=n,不會引起衝突。简单来说就是不建议一开始用n来写
爲了一一對應,x^n自然 m+2=n,不會引起衝突。简单来说就是不建议一开始用n来写
(拉格朗日、凹凸)
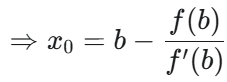 ,证明:a<x0
,证明:a<x0 







参数方程求导

核心:同时/dt
物理应用

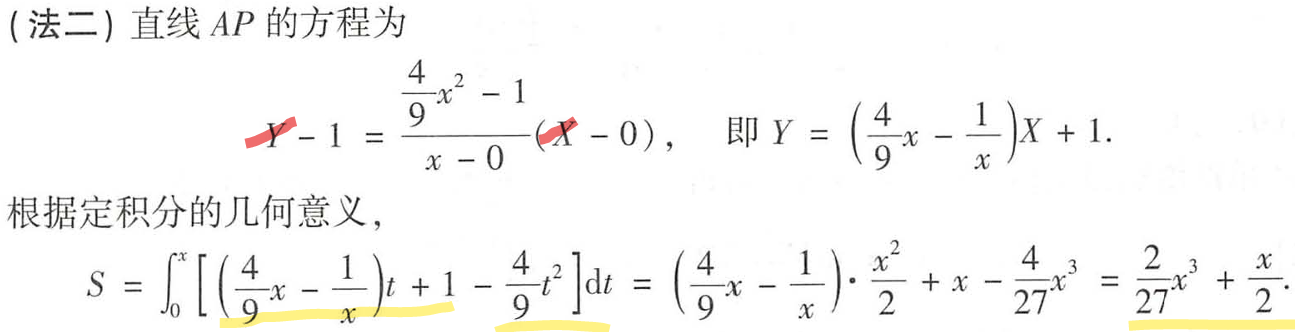
我这里直接求导错了∫f(x,t)dx,直接求导必错。这里是化简求导。还犯了一个错,大小写不分,Y,X,和x,y直接混用,导致AP方程写不出来


二阶导数性质







拐点性质:
拐点
忘记了变号才是拐点。 
偶数次导不等于0就是极值,否则是拐点。 
微分方程
微分方程解的结构
撞大运气了。不知道怎么来的


【解法二】(待定系数法)
- **设方程形式:**设一阶非齐次线性微分方程为 y'+p(x)y=q(x)。

方法三:🚀 从通解公式反推的步骤,太麻烦了。错误直觉。
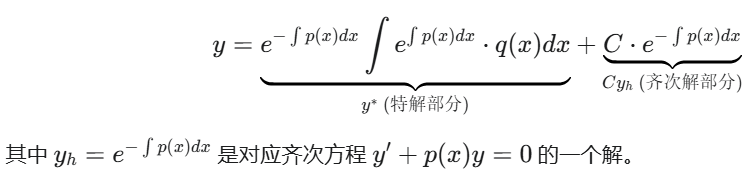
微分方程
原则错误:一阶段和二阶,一阶全是px、qx,但是这个二阶是pq常数。 




二阶齐次
二阶可降阶微分方程的求解\二阶常系数齐次线性微分方程 无法区别
 #偏导数
#偏导数
#物理微分方程

物理应用中,各种变化率是常见物理量,例如温度变化率、体积变化率、速度等 。 找出变化率与其他物理量之间的等量关系,是建立微分方程的关键。本题中, "任一时刻该物体温度对时间的变化率与该时刻物体和介质的温差成正比"这一条件为变化率所满足的等量关系。此外,利用物理学定律建立微分方程也较常见,例如牛顿第二定律。
对于物理应用题,当没有现成的公式可套用的时候,我们常微用微元法来分析自变量的微小变化量所引起的因变量的微小变化量,找出两者之间的等量关系,并建立方程。15.






看错条件,把T当作已知了,理解错题了,感觉就是参数太多了。
难算

绝对值细节,我直接抹去了,未面对虽然没有错

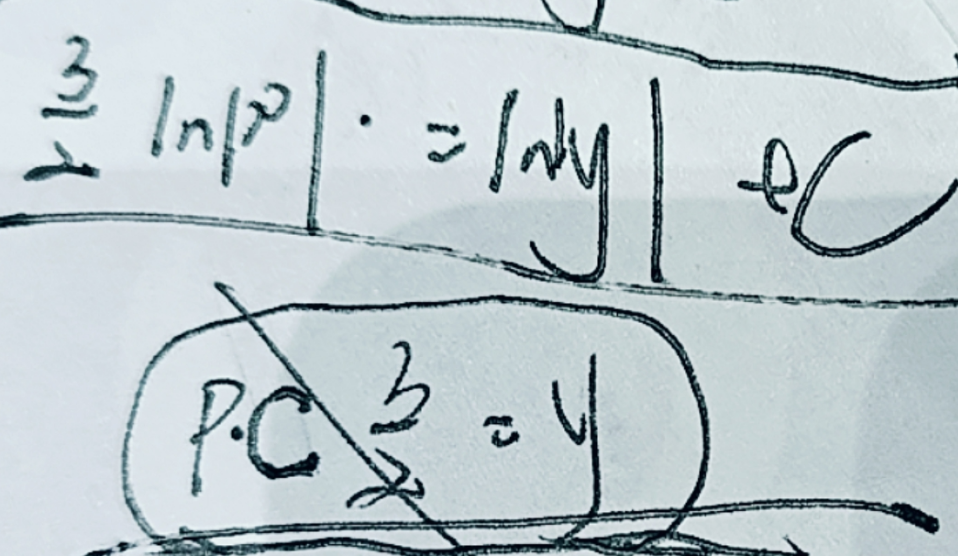 错误
错误
n(n>2)阶常系数齐次线性微分方程

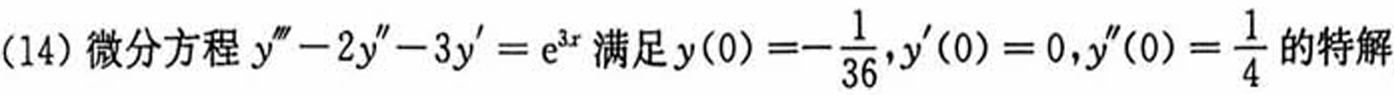

这里回代3导蛮烦,换元试试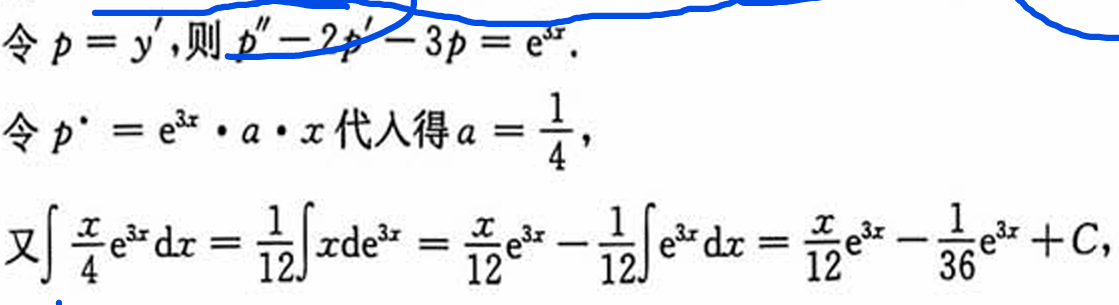
一般解法:

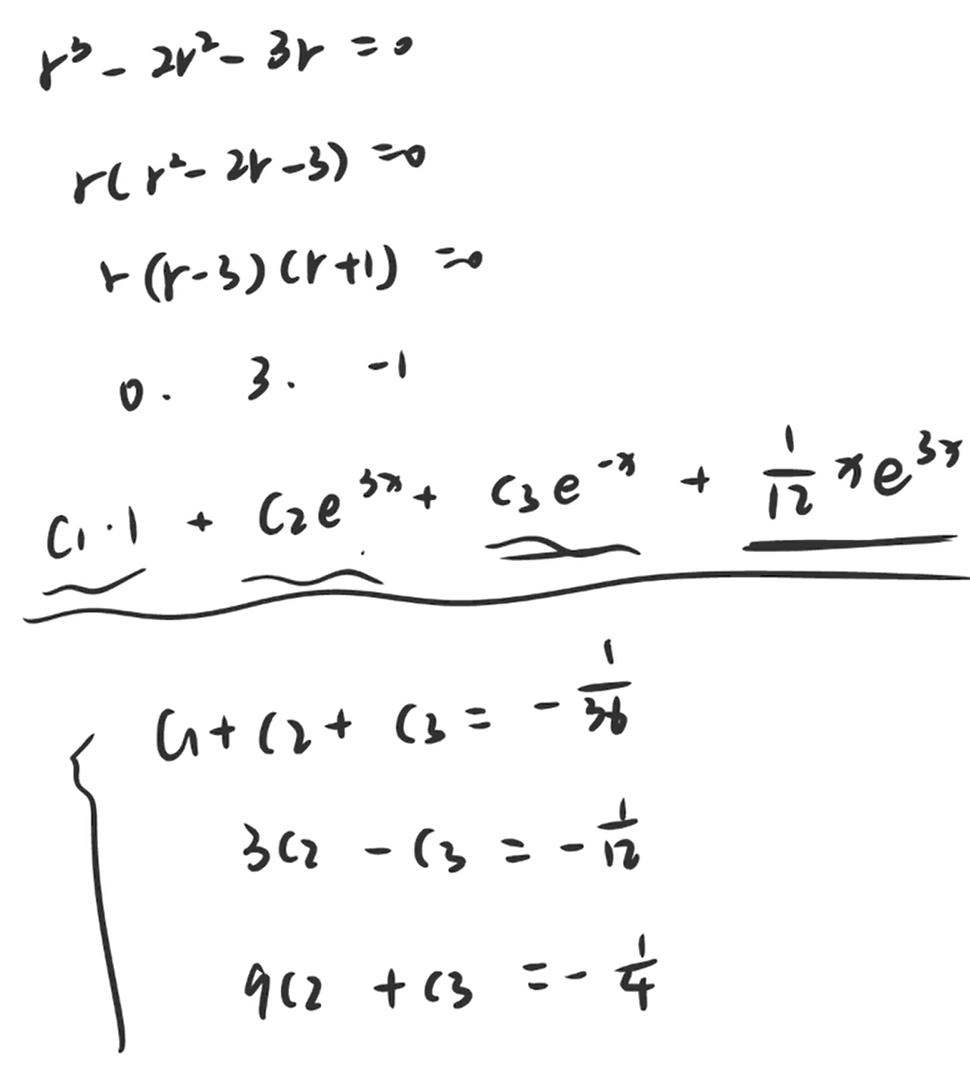
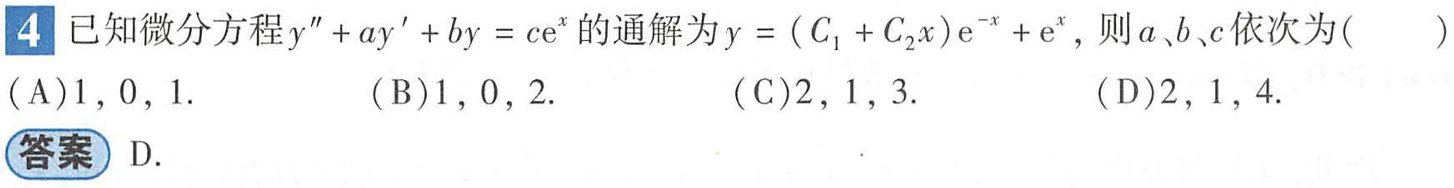



高阶

二重积分
二重积分的计算


最好不要用正弦定理 复杂了r
整体看,消掉一个dy再换元。

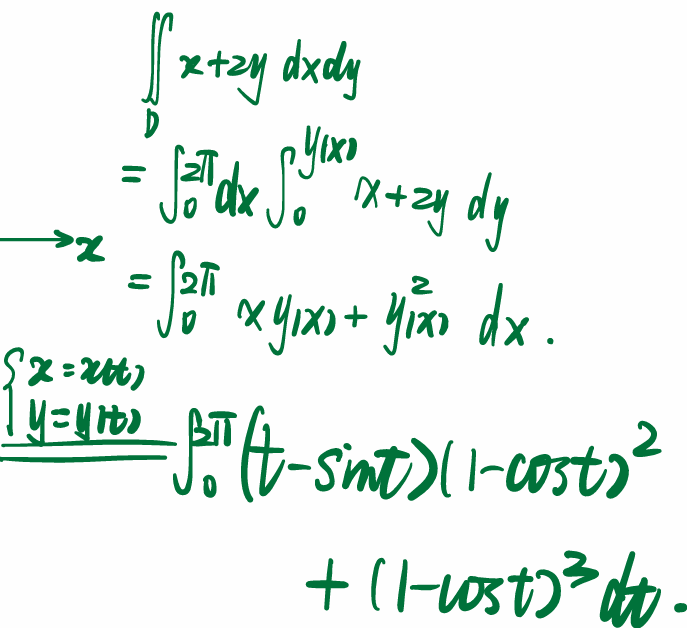
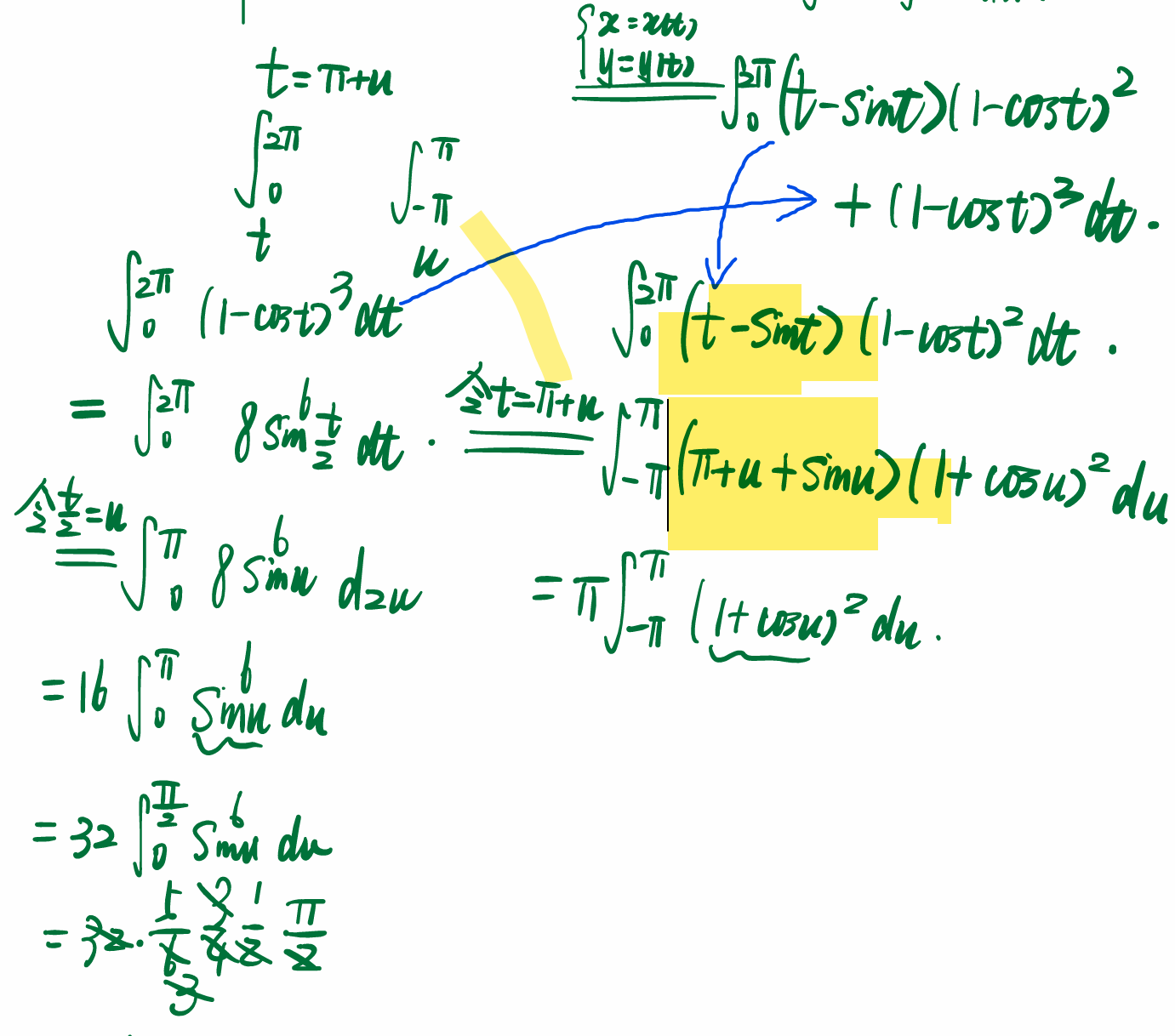
错误做法 但是可以单独来计算,这个答案方法感觉还是很类似: 整体看,消掉一个dy再换元。
但是可以单独来计算,这个答案方法感觉还是很类似: 整体看,消掉一个dy再换元。 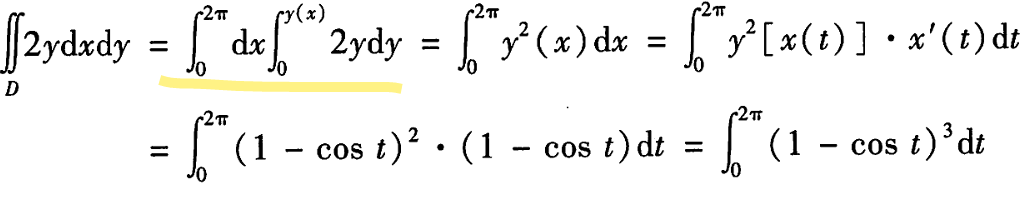
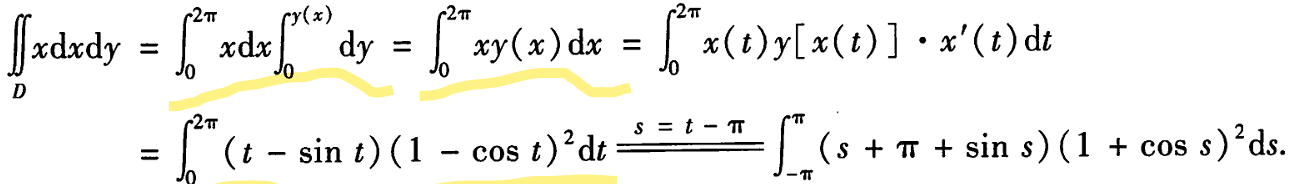
计算问题
绕x轴的旋转V
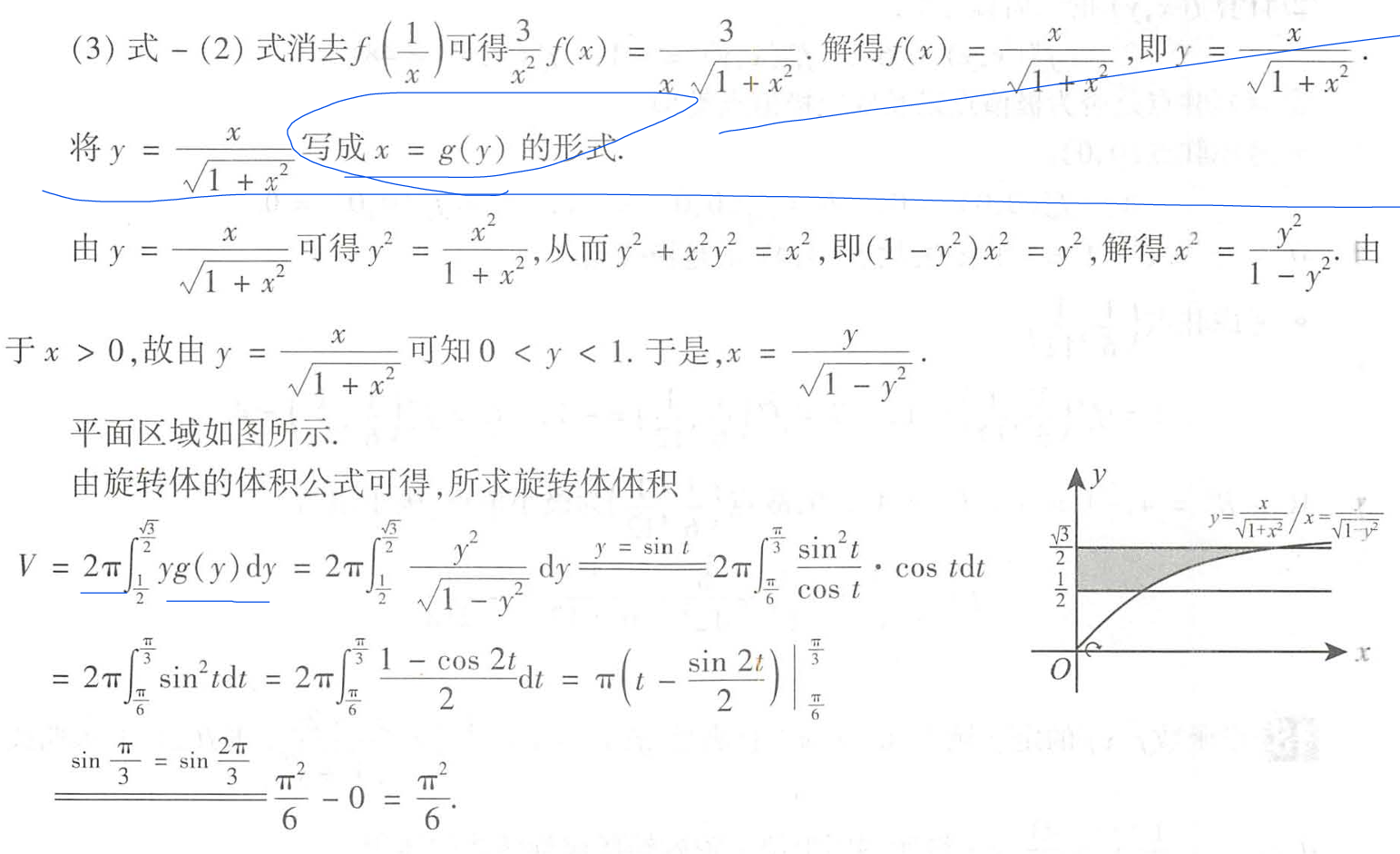

#二重积分-三角积分
难算
∫sec ∫sec^3 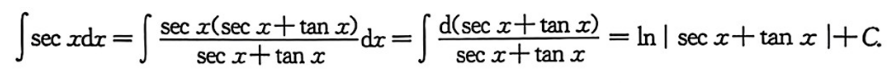
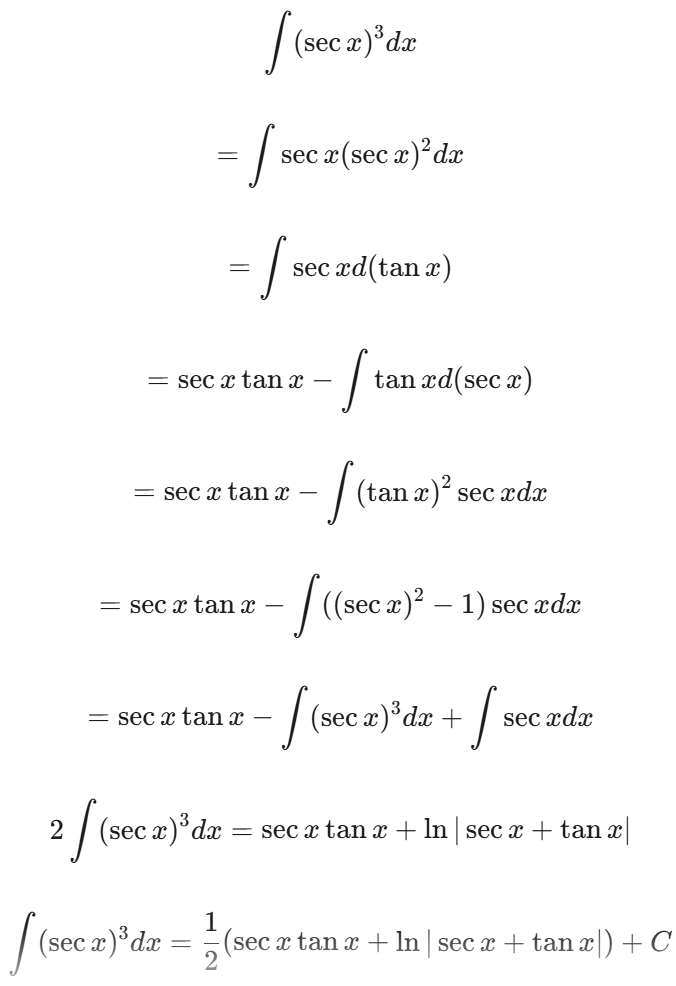

线代
向量组


可逆
六充要:
-
行列式∣A∣≠0
-
秩r(A)=n(满秩)
-
行(列)向量组线性无关。 A 的 行向量组 或 列向量组 线性无关。
-
**齐次方程组:**AX=0只有零解(即 ker(A)={0})
-
**特征值:**0 不是 A 的特征值(即所有特征值均非零)
-
可表示为初等矩阵的乘积
A 可表示为 有限个初等矩阵 的乘积。
7.加个:A-A=AA-=E,交换用法:





范德蒙




要满足 相等但是<3

齐次线性方程组解的结构
行列式按行(列)展开定理: 行列式 D 等于它任意一行(或一列)的元素与它们各自对应的代数余子式乘积之和。错位展开定理: 某一行(或一列)的元素与**另一行(或另一列)**元素的代数余子式乘积之和等于 0。

完全忘了
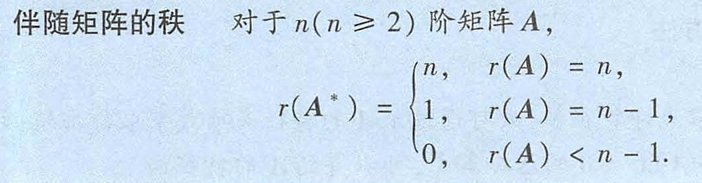 所以rA*=1
所以rA*=1
✅ 第三步:确定解空间的维数
方程组:A∗x=0
是一个齐次线性方程组,系数矩阵是 A∗,秩为 1,变量个数为 4。
根据基础解系维数公式:dim(ker)=n−rank(A∗)=4−1=3
所以,通解是3 个线性无关的解向量的线性组合。
✅ 第四步:找出这 3 个解向量
我们回到关键等式:A∗A=0
将 A 按列分块:A=[α1,α2,α3,α4]
那么:A∗A=A∗[α1,α2,α3,α4]=[A∗α1,A∗α2,A∗α3,A∗α4]=[0,0,0,0]
所以:A∗αi=0对于所有 i=1,2,3,4
结论 A 的每一个列向量 αi 都是 A∗x=0 的解!我们需要从这 4 个解中找出 3 个线性无关的向量作为基础解系。
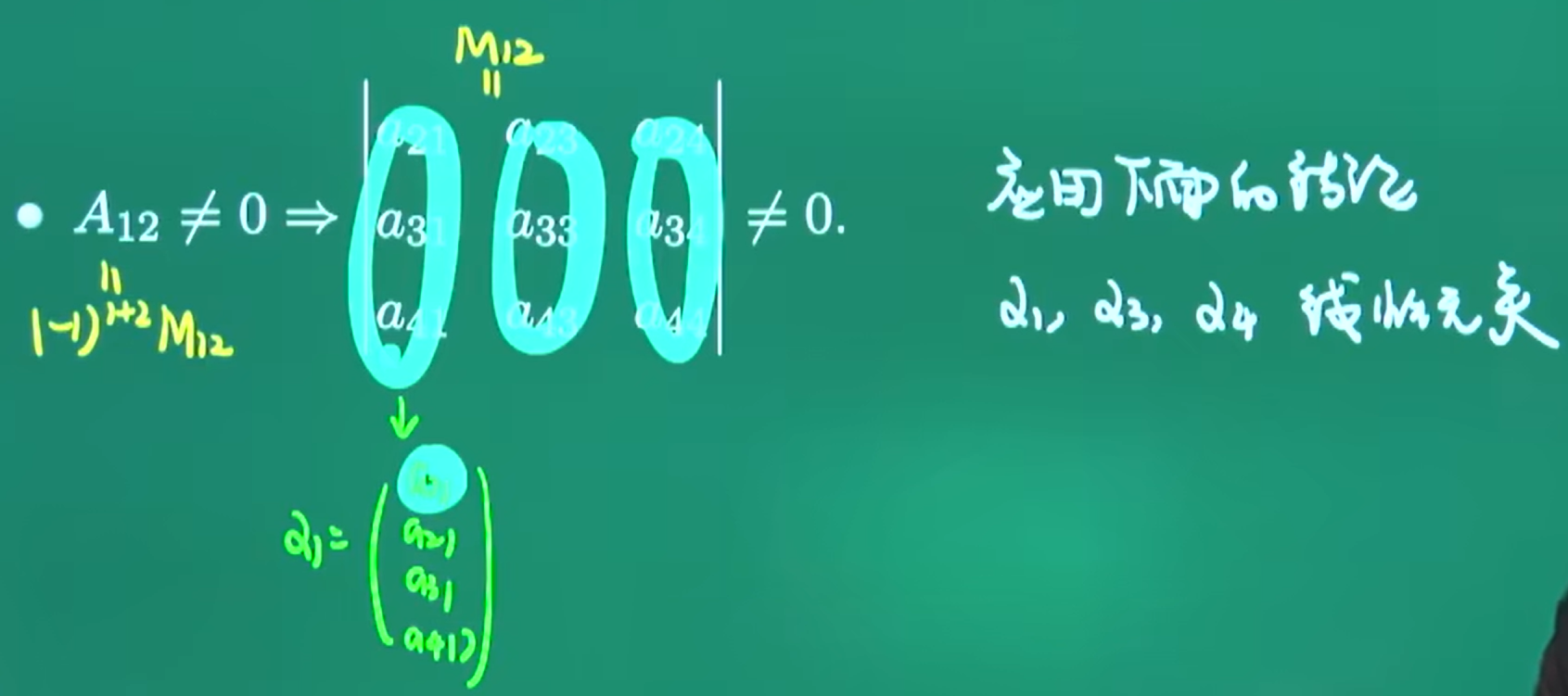



相似


必要条件:
| 性质 | 是否相同 | 理由 |
|---|---|---|
| 行列式 | ✅ 相同 | 相似矩阵的行列式相等: |
| 秩 | ✅ 相同 | 相似变换是线性同构,保持秩不变 |
| 特征方程 | ✅ 相同 | 特征方程定义为 det(λI−A)=0 |
| 特征值 | ✅ 相同(包括重数) | 由特征方程相同直接推出 |
| 迹(trace) | ✅ 相同 | 相似矩阵的迹相等 |
| r(λI − A) | ✅ 相同 | 相似变换下,rλI − A=rλI − B 相似,秩不变 |


| 性质 | 是否相同 | 理由 |
| 行列式 | ✅ 相同 | 相似矩阵的行列式相等: |
| 秩 | ✅ 相同 | 相似变换是线性同构,保持秩不变 |
| 特征方程 | ✅ 相同 | 特征方程定义为 |λI − A| = 0 和 |λI − B| = 0 |
| 特征值 | ✅ 相同(包括重数) | 由特征方程相同直接推出 |
| 迹(trace) | ✅ 相同 | 相似矩阵的迹相等 |
| r(λI − A) | ✅ 相同 | 相似变换下,rλI − A=rλI − B 相似,秩不变 |
|---|

二次型


了解下,这个东西不用算入更快!





方法2
本题的两大陷阱
①a是参数,需要讨论
②平方式之和一定就是标准形吗? 


配两个
算两个P^-1
最后A~对角~B




方法2:



等价
(A|B) 中rA=rB,这个只是等价只有分开处理,不是公共解,公共解才3秩相等


# 线性方程组有解无解

总的来说就是忘了 背为了 rA不等于rB 这是错了
如何求特解:将自由变量为0,然后计算x和b对应上,齐次是自由变量为1、10-01、这些



#数学归纳A^n





思路感觉就是套上第一问结论,无论如何!
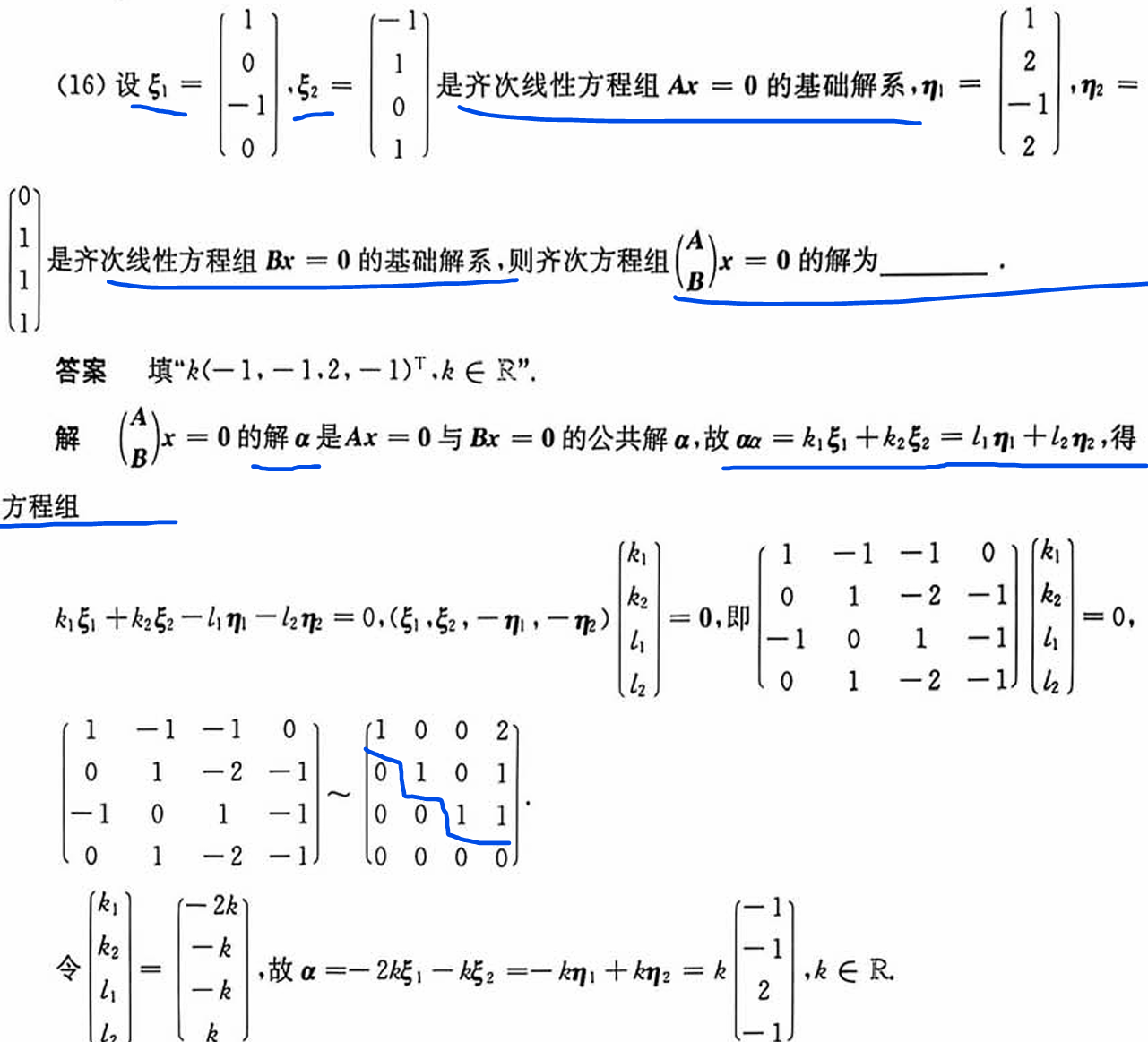
同解
分块矩阵


广义初等变换与初等矩阵:
针对分块矩阵
- 一行(列)左(右)乘矩阵加到另一行(列) 。列子:第一行左乘C为 CA CB 加到第二行
,如果是右边乘只能列变换。一句话:对于分块矩阵,列变换只能右乘,行变换只能左乘
- 2行(列)互换
- 一行(列)左(右)乘可逆矩阵 。类比(3):一个非零常数乘矩阵的某一行(列);例如:将第一行左乘一个可逆矩阵 E
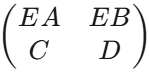
初等变换:
(1)将矩阵的某一行(列)的k倍加到另一行(列)。
(2)互换矩阵中某两行(列)的位置;
(3)一个非零常数乘矩阵的某一行(列);
等价合同相似


合同
-
实对称矩阵 的合同矩阵仍是实对称矩阵。
-
实对称矩阵 一定可以被正交相似 于一个对角矩阵/\ (即由其特征值组成的对角矩阵)。QTAQ=/\,注意这里QT=Q-,所以这里也是相似合同。
-
(充要条件): 两个实对称矩阵(或二次型)合同的充要条件是它们具有相同的正、负惯性指数(即相同的正特征值个数和负特征值个数)。
-
秩与相似: 相似矩阵的秩相等,合同矩阵的秩也相等。

AP=B求P

第一题我错了-用的行列式相等错了。使用秩相等 r(A) = r(B)
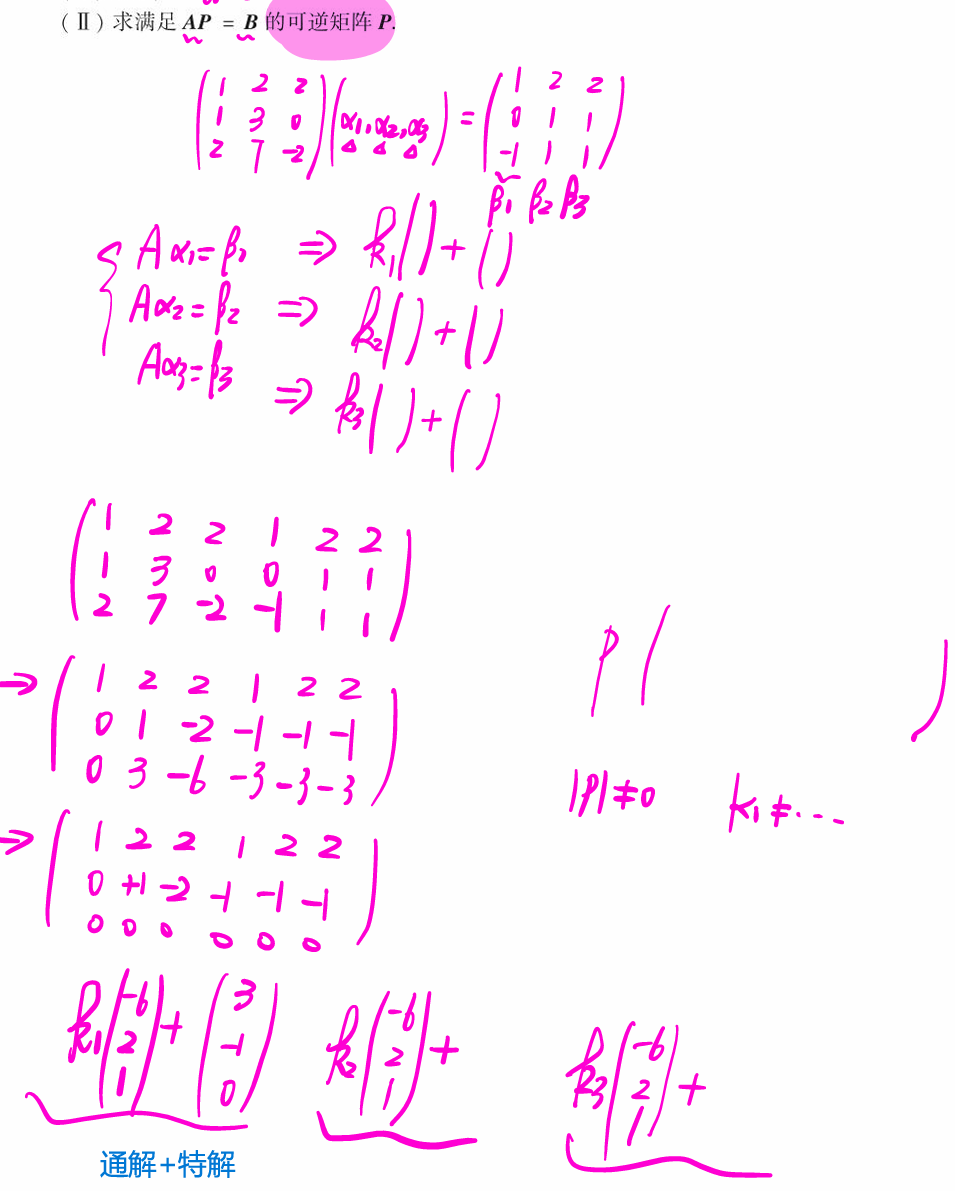


线代








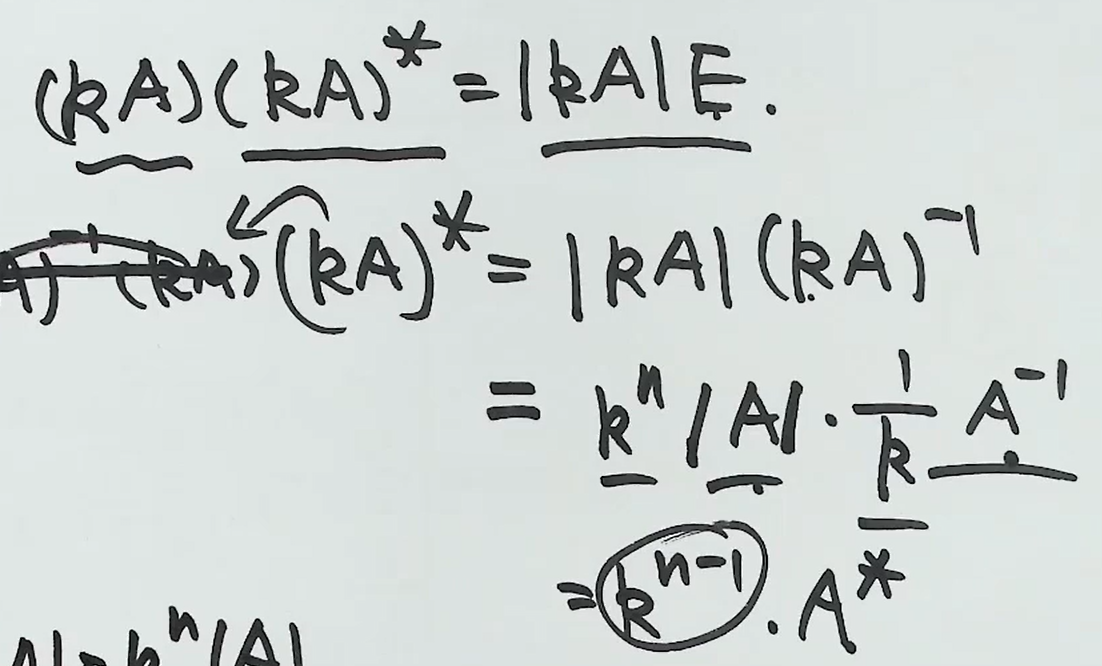




已知条件:
A 是 3 \\times 3 实对称矩阵。
A X_1 = \\beta, A X_2 = \\beta,其中 X_1 = (a, b, c)\^T, X_2 = (a, b+1, c-1)\^T,且 a \\neq 0。
\\operatorname{tr}(A\^\*) = 2
目标:
求 A\^\* (伴随矩阵) 及 (A\^\*)\^n。
- 1.对于AX=b的所有解向量,其中线性无关的解向量个数一定为n-r+1
- 2.对于AX=b的任意个解向量,其中线性无关的解向量个数至多为n-r+1



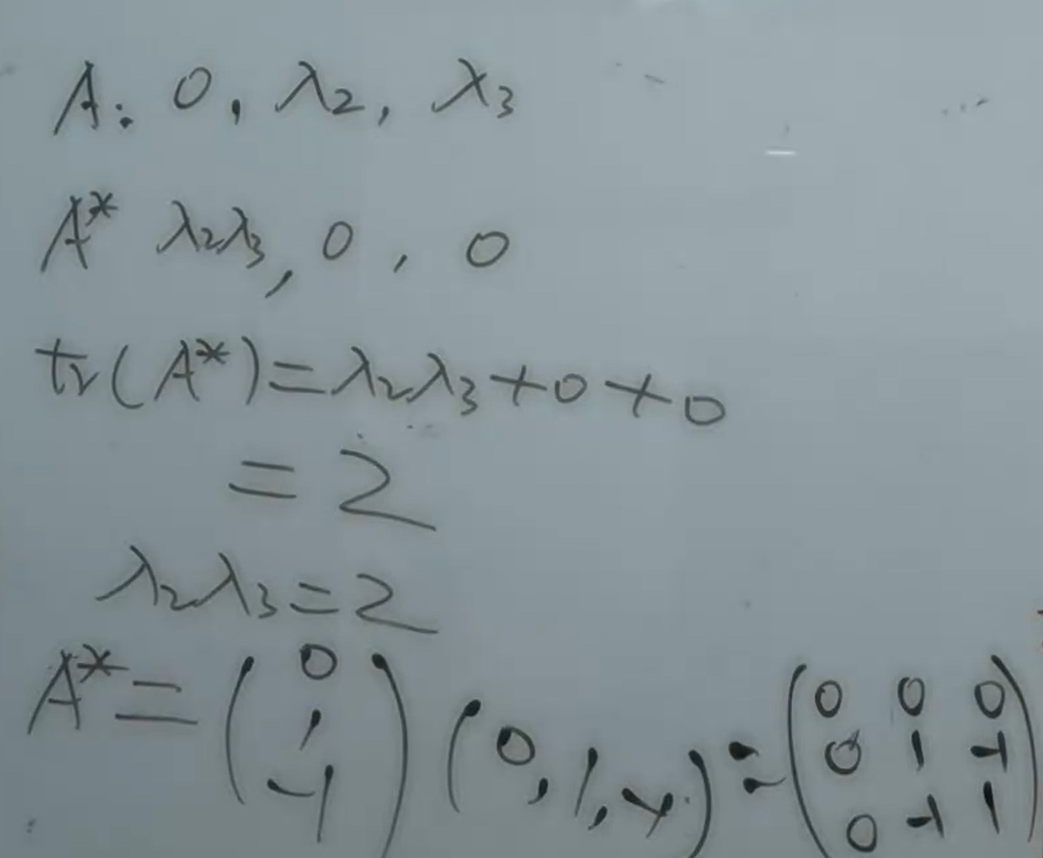




证明题