文章目录
- 一、LLaMA架构
-
- [1. 基本介绍](#1. 基本介绍)
- [2. 技术路线图:对比Transformer](#2. 技术路线图:对比Transformer)
- [3. 思考](#3. 思考)
-
- [3.1 为什么LLaMA使用的是Transformer中的Decoder解码器?](#3.1 为什么LLaMA使用的是Transformer中的Decoder解码器?)
- [3.2 为什么RoPE只给Q和K做位置编码?](#3.2 为什么RoPE只给Q和K做位置编码?)
- 二、重要组成部分
-
- [1. Embedding](#1. Embedding)
- [2. RMSNorm均方根层归一化](#2. RMSNorm均方根层归一化)
-
- [2.1 Layer Normalization 和 Batch Normalization 的区别](#2.1 Layer Normalization 和 Batch Normalization 的区别)
- [2.2 LN与RMSNorm的区别](#2.2 LN与RMSNorm的区别)
- [3. 旋转位置编码Rotary Positional Encodings](#3. 旋转位置编码Rotary Positional Encodings)
- [4. Self-Attention(Grouped Multi-Query Attetion with KV cache)](#4. Self-Attention(Grouped Multi-Query Attetion with KV cache))
-
- [4.1 基本概念](#4.1 基本概念)
- [4.2 工作原理](#4.2 工作原理)
- [4.3 模型代码](#4.3 模型代码)
- [4.3.1 分组查询注意力](#4.3.1 分组查询注意力)
- [4.3.2 注意力机制](#4.3.2 注意力机制)
- [5. 门控前馈神经网络FFN with SwiGLU](#5. 门控前馈神经网络FFN with SwiGLU)
-
- [5.1 门控FFN](#5.1 门控FFN)
- [5.2 SwiGLU激活函数](#5.2 SwiGLU激活函数)
- [5.3 SiLU激活函数](#5.3 SiLU激活函数)
- [5.4 LLaMA架构的门控FFN代码](#5.4 LLaMA架构的门控FFN代码)
- [6. 混合专家网络用于FFN层](#6. 混合专家网络用于FFN层)
-
- [6.1 MoE原理](#6.1 MoE原理)
- [6.2 MoE与Transformer或LLaMA架构是什么关系?MoE的优势](#6.2 MoE与Transformer或LLaMA架构是什么关系?MoE的优势)
- [6.3 MoE训练流程](#6.3 MoE训练流程)
- [6.4 MoE训练阶段和推理阶段的不同](#6.4 MoE训练阶段和推理阶段的不同)
- [6.5 MoE模型代码](#6.5 MoE模型代码)
一、LLaMA架构
1. 基本介绍
《LLaMA: Open and Efficient Foundation Language Models》论文地址:https://arxiv.org/abs/2302.13971
LLaMA并非一个全新的、从零开始设计的架构。它巧妙整合并验证了多个当时业界公认的最高效的Transformer改进方案。例如:
- 预归一化:使用RMSNorm层进行归一化,提高训练稳定性。
- SwiGLU激活函数:替代传统的Relu,提升模型表达能力。
- 旋转位置编码:使用RoPE,能更好地处理长序列。
2. 技术路线图:对比Transformer
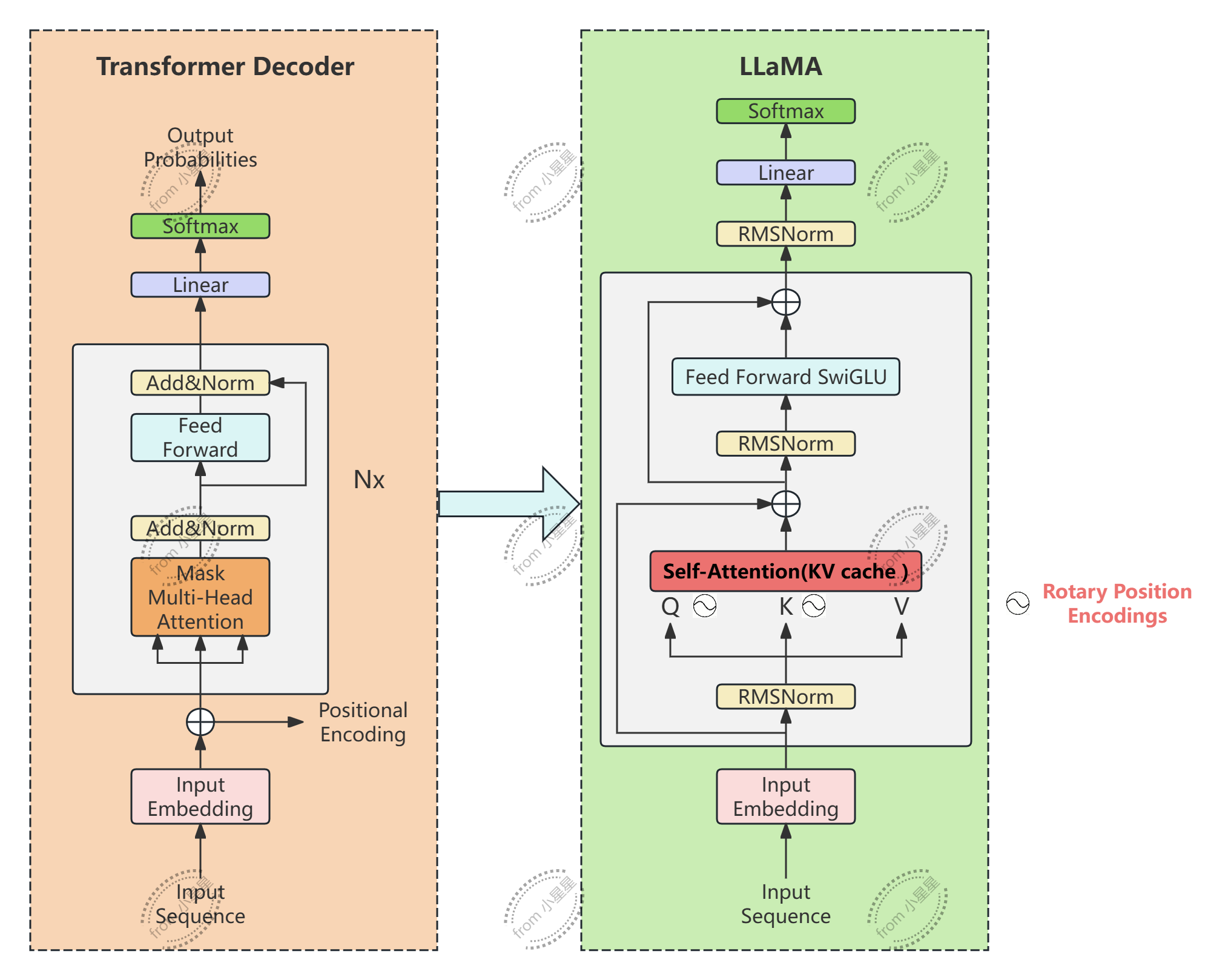
从对比图可以看出,LLaMA架构在位置编码和自注意力机制上做了较大的调整。Transformer-Decoder中的位置编码不再是给input embedding做改进,而是给经过QK做编码。为了提升计算效率,LLaMA的自注意机制采用的是KV缓存:加入多头为8个头,此时我们要求将KV分别生成两个矩阵并将这两个矩阵保存,针对不同的Q,都是使用缓存的这两个KV来计算。
3. 思考
3.1 为什么LLaMA使用的是Transformer中的Decoder解码器?
- 任务需求的匹配:自回归生成。Decoder的在训练时使用因果注意力掩码(Causal Attention Mask) ,也称为前瞻掩码(Look-ahead Mask),在计算注意力权重矩阵时,会做一个时间窗静止当前单词对后续单词进行询问,在预测下一个单词的时候,只利用之前的所有词。这本是就是一个天然、高效的文本生成器结构。Encoder模型(BERT)主要擅长理解型任务(eg. 文本分类、文本匹配、语义相似度),而不是生成类任务。这个
- 架构效率:在先沟通的计算预算下,一个巨型纯Decoder模型可能比一个同等规模的Encoder-Decoder模型在生成任务上表现更好,因为所有参数都聚焦于同一个目标。

Bert是Encoder-only模型,GPT是Decoder-only模型,上图是具体的对比。
3.2 为什么RoPE只给Q和K做位置编码?
- 注意力分数的计算原理: 注意力机制的核心是"注意力分数"矩阵(Q·K T)计算的是查询与键的匹配度或相关性。这个相关性必须包含位置信息,因为一个词与另一个词的相关性高度依赖于它们之间的相对位置(例如,"apple"在"eat"前面和后面含义完全不同)。因此,位置编码的核心目的是为了让模型在计算"谁应该关注谁"(Q·K^T)时,能够感知到位置关系。
- 注意力分数的计算原理:RoPE是一种相对位置编码,它通过旋转矩阵将位置信息注入到Q和K中,得到的点积(Q_i· K_ j ^ T)结果只依赖于相对位置 i - j,而不是绝对位置 i 或 j 。如果我们将RoPE也应用到V上,可能会扭曲V本身所携带的语义信息,且是没必要的,因为softmax分数已经包含了位置感知,这个分数决定了V的权重,旋转V并不会改变"该关注哪个token的决策"。
二、重要组成部分
1. Embedding
在PyTorch,nn.Embedding层是用于处理离散数据的关键组件,主要功能是将输入的整数索引映射到连续的高维向量空间中,即将索引转化为嵌入向量。
python
import torch
import torch.nn as nn
# 定义Embedding层
embedding = nn.Embedding(10, 3) # num_embeddings=10, embedding_dim=3
# 输入索引
input_indices = torch.tensor([1, 2, 3])
# 获取嵌入向量
output = embedding(input_indices)
print(output)2. RMSNorm均方根层归一化
2.1 Layer Normalization 和 Batch Normalization 的区别
最重要的区别在于计算均值和方差的方向不同,LN在一次更新迭代中统计同一层内的所有神经元节点的输出分布(同一个样本下);BN是在一个Batch内统计某特定神经元的输出分布(跨样本)。
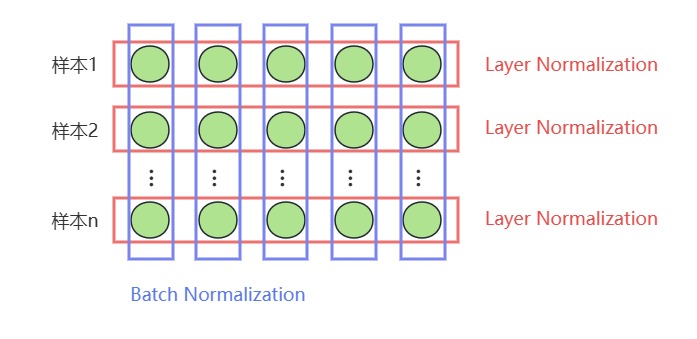
在NLP任务中会经常处理长度不同的句子,使用LN时可以不需要考虑其他样本的长度是否,如果按照Batch维度进行统计的话,会存在一定问题:为了让样本均衡,一般会对样本进行裁剪或者填补,里面一定有大量为0的特征值,因此在计算特征均值和方差肯定会受到影响。
2.2 LN与RMSNorm的区别

那么问题来了,为什么通过RMSNorm可以起到归一化的作用?
首先,要先回顾下归一化层的作用。归一化层是为了防止梯度爆炸/消失,实现手段是控制尺度,而非严格的中心化。RMS(x) 衡量的是向量的"典型幅度",类似于向量的L2范数(相差一个根号n因子)。经过RMSNorm后,输出向量的RMS值为1:RMS(RMSNorm(x))=1,这就强制输出的尺寸保有一致性。
python
import torch
import torch.nn as nn
class RMSNorm(nn.Module):
def __init__(self, dim: int, eps: float = 1e-8):
super().__init__()
self.eps = eps
self.weight = nn.Parameter(torch.ones(dim))
def _norm(self, x):
# 计算 RMS 归一化因子
rms = torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)
return x * rms
def forward(self, x):
# 保持计算精度为float,然后转换回输入类型
output = self._norm(x.float()).type_as(x)
return output * self.weight
# 正确使用方式
x = torch.randn(2, 3, 768)
rmsnorm = RMSNorm(dim=768, eps=1e-6) # 创建实例
norm = rmsnorm(x) # 通过实例调用
print("输出形状:", norm.shape)
#输出: torch.Size([2, 3, 768])3. 旋转位置编码Rotary Positional Encodings

这段代码不用记了,记不住的···,知道旋转位置编码的原理即可。
python
#定义频率计算
def precompute_pos_cis(dim: int, max_position: int, theta: float = 10000.0):
#频率
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
#位置编码m
m = torch.arange(max_position, device=freqs.device)
#频率乘以位置编码、外积
freqs = torch.outer(m, freqs).float()
#
pos_cis = torch.polar(torch.ones_like(freqs), freqs)
return pos_cis
#将频率用于q、k矩阵
def apply_rotary_emb(xq, xk, pos_cis):
def unite_shape(pos_cis, x):
ndim = x.ndim
assert 0 <= 1 < ndim
print(pos_cis.shape)
print(x.shape[1])
print(x.shape[-1])
assert pos_cis.shape == (x.shape[1], x.shape[-1])
shape = [d if i == 1 or i == ndim - 1 else 1 for i, d in enumerate(x.shape)]
return pos_cis.view(*shape)
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
pos_cis = unite_shape(pos_cis, xq_)
xq_out = torch.view_as_real(xq_ * pos_cis).flatten(3)
xk_out = torch.view_as_real(xk_ * pos_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk)4. Self-Attention(Grouped Multi-Query Attetion with KV cache)
4.1 基本概念
KV缓存(Key-Value Cache)是Transformer模型自回归生成任务中的一个重要加速技术。在文本生成任务中,每一步生成一个新的token,这个新的token跟之前所有的tokens一起重新输入到模型中,预测下一个token。对于每一步的生成,模型会重新计算所有tokens的注意力分数,这个过程是非常耗时的,因此,为了避免重复计算注意力层中的K和V,在生成后续token时,模型只需要计算token的Query,直接调用缓存中的Key和Vaule。
4.2 工作原理
KV缓存大部分时候适用于推理过程中。
-
初始化:
当模型开始时,模型计算输入序列的Key和Value,并将这些计算结果缓存起来,保存在内存中。大部分时候,每个注意力层都会有一对Key-Value缓存,这个缓存是自回归的每次循环中共用的。还有一种做法是:在多头注意力机制中,只保留一个头或者两个头以上的KV值,并共享给所有头使用。
-
生成过程:
当生成下一个token时,模型不需要重新计算前面已经生成的token的Key和Value始终保持更新,包含所有已生成的tokens。最终会包含所有生成序列的Key和Value。
-
更新缓存:
对于每一个生成步骤,模型还会将当前生成的token的Key和Value加入缓存,确保缓存中的Key和Value始终保持更新,能够包含所有已经生成的tokens。
-
加速效果:
由于每个生成步骤只需要计算当前token的Query,而不需要重新计算整个序列的Key和Value,这大大减少了计算量。随着序列长度增加,缓存的使用能够显著减少时间复杂度,使生成过程更快。
4.3 模型代码
4.3.1 分组查询注意力
多个查询头共享一组K、V头。
场景:假设有
- 查询头数(n_q_heads):8
- KV缓存头数量(n_kv_heads):2
- 每个头的维度(head_dim):64
那么我们需要让:
- 这里每个KV需要被8/2=4个查询头共享
python
def repeat_kv(x:torch.Tensor, n_rep:int):
'''
:param x: tensor , shape (bs, slen, n_kv_heads, head_dim)
:param n_rep: 重复次数
:return:
'''
bs, slen, n_kv_heads, head_dim = x.shape
#bs: 批次大小 (batch size)
# slen: 序列长度 (sequence length)
# n_kv_heads: KV 头的数量 (number of key-value heads)
# head_dim: 每个头的维度大小 (dimension size of each head)
if n_rep == 1:
return x
return (
x[:, :, :, None, :]
.expand(bs, slen, n_kv_heads, n_rep, head_dim)
.reshape(bs, slen, n_kv_heads * n_rep, head_dim)
)4.3.2 注意力机制
python
import torch
import torch.nn as nn
from Config import LMConfig
import torch.nn.functional as F
import math
from typing import Optional, Tuple
from dataclasses import dataclass
@dataclass
class LMConfig:
dim: int = 4096
n_heads: int = 32
n_kv_heads: Optional[int] = None
max_seq_len: int = 2048
dropout: float = 0.1
flash_attn: bool = True
def __post_init__(self):
if self.n_kv_heads is None:
self.n_kv_heads = self.n_heads
#旋转位置编码
def apply_rotary_emb(
xq: torch.Tensor,
xk: torch.Tensor,
freqs_cis: torch.Tensor
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
应用旋转位置编码到查询和键上
"""
# 将复数转换为实数和虚数部分
xq_complex = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_complex = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
# 应用旋转
freqs_cis = freqs_cis.unsqueeze(0).unsqueeze(2) # 添加batch和head维度
xq_out = torch.view_as_real(xq_complex * freqs_cis).flatten(3)
xk_out = torch.view_as_real(xk_complex * freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk)
#分组查询注意力
def repeat_kv(x: torch.Tensor, n_rep: int) -> torch.Tensor:
"""
重复KV张量以匹配查询头的数量
"""
batch_size, seq_len, n_kv_heads, head_dim = x.shape
if n_rep == 1:
return x
# 扩展维度并重复
x = x[:, :, :, None, :] # 添加一个维度用于重复
x = x.expand(batch_size, seq_len, n_kv_heads, n_rep, head_dim)
# 重新塑形
x = x.reshape(batch_size, seq_len, n_kv_heads * n_rep, head_dim)
return x
# 最后定义Attention类
class Attention(nn.Module):
def __init__(self, args: LMConfig):
super().__init__()
# 先确定n_kv_heads的值,如果设置了单独的n_kv_heads,就执行多头共享机制
# 如果没设置kv_heads,就意味着全部的头都要执行kv缓存,此时n_kv_heads = n_heads
self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads
# 检验,n_heads能否被n_kv_heads除尽
assert args.n_heads % self.n_kv_heads == 0
# 设置头数、kv缓存头数和重复次数
self.n_local_heads = args.n_heads
self.n_local_kv_heads = self.n_kv_heads
self.n_rep = self.n_local_heads // self.n_local_kv_heads
# 设置每个头上的特征维度
self.head_dim = args.dim // args.n_heads
# 设置权重层,当 x 的结构为 (seq_len, d_model)时
# 常规的Q、K、V矩阵的结构应该与 X 一致,也是 (seq_len, d_model)
# 因此常规的 w 应该是 (d_model,d_model)结构
# 在多头注意力中,w 应该是 (d_model, d_model/n_heads)
# 在具有kv缓存的情况下,我们是对所有头上的注意力并行计算
# 因此Q的权重应该是(d_model, d_model)
# K和V的权重应该是(d_model, d_model/n_heads * n_kv_heads)
self.wq = nn.Linear(args.dim, args.n_heads * self.head_dim, bias=False)
self.wk = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)
self.wv = nn.Linear(args.dim, self.n_kv_heads * self.head_dim, bias=False)
# 输出层上的O的权重不受影响,是(d_model, d_model)
self.wo = nn.Linear(args.n_heads * self.head_dim, args.dim, bias=False)
# 设置kv缓存初始值
self.k_cache, self.v_cache = None, None
# 设置注意力和残差连接上的dropout层和dropout比例
self.attn_dropout = nn.Dropout(args.dropout)
self.resid_dropout = nn.Dropout(args.dropout)
self.dropout = args.dropout
# flash attention
# print("WARNING: using slow attention. Flash Attention requires PyTorch >= 2.0")
self.flash = hasattr(torch.nn.functional, 'scaled_dot_product_attention') and args.flash_attn
# 设置decoder专用前瞻掩码
# 注意,前瞻掩码是用于QK.T矩阵的
mask = torch.full((1, 1, args.max_seq_len, args.max_seq_len), float("-inf"))
mask = torch.triu(mask, diagonal=1)
# buffer用于保存神经网络中除了权重之外、需要被保存的静态数据们
# 比如掩码矩阵、比如位置编码中的频率等等编码表
# "mask"我们指定的buffer名称,我们可以通过self.mask来调出掩码矩阵
self.register_buffer("mask", mask, persistent=False)
# 设置旋转位置编码中的频率计算
def _precompute_pos_cis(self, dim: int, max_position=10000, theta: float = 10000.0):
freqs = 1.0 / (theta ** (torch.arange(0, dim, 2)[: (dim // 2)].float() / dim))
m = torch.arange(max_position, device=freqs.device)
freqs = torch.outer(m, freqs).float()
pos_cis = torch.polar(torch.ones_like(freqs), freqs)
return pos_cis
def forward(self, x: torch.Tensor, kv_cache=False):
# 作为注意力机制,被输入的x就是原始数据x
# 结构为 (bs, seq_len, d_model)
bsz, seqlen, _ = x.shape
# 无论是否执行KV缓存,Q的求解是不变的
xq = self.wq(x)
# 如果是训练模式下,K和V照常求解
if self.train():
# 将x输入线性层、转换为初始的K和V
# 但是只需要n_kv_heads个头的部分
xk, xv = self.wk(x), self.wv(x)
# 如果是推理模式,且kv_cache设置是打开的
# 那要判断现在是否是初次预测
if kv_cache and self.eval():
# kv缓存是否还是None?已经存在了吗?
if all(cache is not None for cache in (self.k_cache, self.v_cache)):
# 如果不是None,说明不是初次预测了,此时需要的是缓存更新
xk_new_token = self.wk(x[:, -1, :]).unsqueeze(1)
xv_new_token = self.wv(x[:, -1, :]).unsqueeze(1)
xk = torch.cat((self.k_cache, xk_new_token), dim=1)
xv = torch.cat((self.v_cache, xv_new_token), dim=1)
else:
# 如果k和v缓存中有一个为None,说明是初次预测
xk, xv = self.wk(x), self.wv(x)
# 生成xk和xv后,把结果保存到缓存中
self.k_cache, self.v_cache = xk, xv
# 为了更省内存,我们要将数据结构重新整理后适应位置编码的结构
# 可以将该流程命名为"多头旋转位置编码"
xq = xq.view(bsz, seqlen, self.n_local_heads, self.head_dim)
xk = xk.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
xv = xv.view(bsz, seqlen, self.n_local_kv_heads, self.head_dim)
# 在Q和K上执行旋转位置编码
pos_cis = self._precompute_pos_cis(self.head_dim, seqlen)
xq, xk = apply_rotary_emb(xq, xk, pos_cis)
# 将k矩阵和v矩阵进行重复
xk = repeat_kv(xk, self.n_rep) # (bs, seqlen, n_local_heads, head_dim)
xv = repeat_kv(xv, self.n_rep) # (bs, seqlen, n_local_heads, head_dim)
# 矩阵乘法计算注意力分数时,要将n_heads作为第二维度
# 因为实际要进行乘法的应该时 (seqlen, head_dim) 这样的二维表
# transpose交换维度,结构变为(bs, n_local_heads, seqlen, head_dim)
xq = xq.transpose(1, 2)
xk = xk.transpose(1, 2)
xv = xv.transpose(1, 2)
# 如果使用flash attention的话
# 就调用nn.functional下面的点乘注意力计算方法
if self.flash and seqlen != 1:
output = torch.nn.functional.scaled_dot_product_attention(xq, xk, xv
, attn_mask=None # 这里是padding掩码
, dropout_p=self.dropout if self.training else 0.0
, is_causal=True # 这里是自动化的前瞻掩码
)
else:
# 不使用flash attention,就自己计算
# 这里的transpose是对最后两个维度的转置
scores = torch.matmul(xq, xk.transpose(2, 3)) / math.sqrt(self.head_dim)
# 在注意力分数上放上掩码
# 如果有kv缓存的话,现在我们的kv矩阵可能会比掩码矩阵要大了
# 获取缓存的长度
cache_len = self.k_cache.shape[1] if self.k_cache is not None else 0
total_len = cache_len + 1 # 当前总长度,等于历史缓存长度 + 当前序列长度
# 检查是否需要扩展掩码矩阵
if total_len > self.mask.shape[-1]:
# 动态生成新的掩码,大小为 (seq_len + cache_len, seq_len + cache_len)
new_mask = torch.full((1, 1, total_len, total_len), float("-inf")).to(x.device)
new_mask = torch.triu(new_mask, diagonal=1) # 生成前瞻掩码
self.mask = new_mask # 更新掩码矩阵
scores = scores + self.mask[:, :, :seqlen, :seqlen]
# 对最后一个维度求解softmax
scores = F.softmax(scores.float(), dim=-1).type_as(xq)
scores = self.attn_dropout(scores)
output = torch.matmul(scores, xv) # (bs, n_local_heads, seqlen, head_dim)
# 最后再将结构转回来,并且将n_heads中的所有信息合并
# contiguous() 用于确保张量在内存中的存储是连续的
# 特别是在经过某些操作(如 transpose)后,这对后续的 view() 等操作至关重要,以避免错误
output = output.transpose(1, 2).contiguous().view(bsz, seqlen, -1)
# 注意力机制的输出
output = self.wo(output)
output = self.resid_dropout(output)
return output
# 测试
config = LMConfig(dim=768, n_heads=12, n_kv_heads=4, max_seq_len=512)
attention = Attention(config)
x = torch.randn(2, 16, config.dim) # batch_size=2, seq_len=16
output = attention(x)
print(f"输出形状: {output.shape}")
# 应该输出: torch.Size([2, 16, 768])5. 门控前馈神经网络FFN with SwiGLU
5.1 门控FFN
与常见的前馈神经网络相比,LLaMA架构中的前馈神经网络有一些独特的设计。
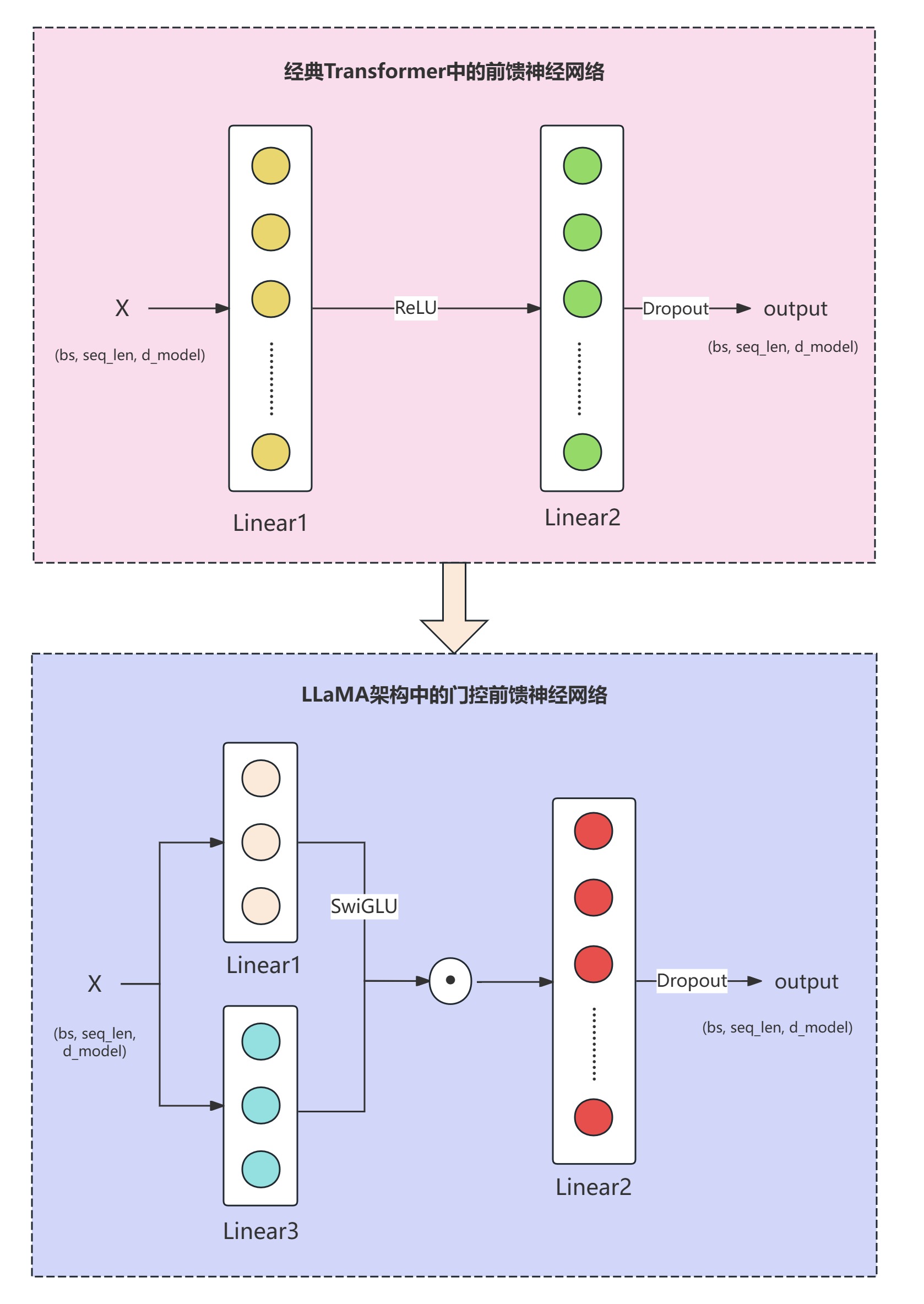
典型的前馈神经网络是:output = Linear2(Activation (Linear1(x))。
LLaMA中的前馈神经网络是:output = Linear2(SwiGLU(Linear1(x)⊙(Linear3(X)))。其中SwiGLU(Linear1(x) ) 和 Linear3(X) 两条路线性路径的输出逐元素相乘(⊙),实现了信息的动态控制。这种门控结构类似于在 LSTM 和 GRU 等门控循环网络中的思想,但它被应用在 Transformer 的前馈网络(FFN)层中,用于增强网络的非线性表达能力和训练效率。
门控机制为何高效?
门控机制(Gating Mechanism) 是深度学习中的一种重要设计,它通过信息流的动态选择,提升了模型的表达能力和训练效率。相比于单纯的线性变化和激活函数,门控机制更加灵活,使模型能够根据输入数据的特性决定哪些信息需要传递、哪些信息需要抑制。
| 优势 | 解释 |
|---|---|
| 避免冗余计算 | 只让有用的信息通过,抑制无关信息,提升计算效率 |
| 强化非线性表达能力 | 通过多条路径组合增强模型的表达能力 |
| 改善梯度流动 | 减少梯度消失问题,提高深层网络的训练效率 |
| 自适应学习能力 | 根据不同输入动态选择信息流,提高任务适用性 |
| 多任务场景中的共享能力 | 在多任务或多模态模型中更智能地控制信息流动路径 |
5.2 SwiGLU激活函数
SiwGLU激活函数的基本形式为:
SwiGLU(x)=GELU(W1aX) ⊙ (W1bX)
python
# 定义 ReLU 激活函数及其梯度
def relu(x):
return np.maximum(0, x)
def relu_derivative(x):
return np.where(x > 0, 1, 0)
# 定义 GELU 激活函数及其梯度
def gelu(x):
return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))
def gelu_derivative(x):
tanh_term = np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3))
sech2_term = 1 - tanh_term ** 2 # tanh 导数
return 0.5 * (1 + tanh_term + np.sqrt(2 / np.pi) * x * (1 + 3 * 0.044715 * x**2) * sech2_term)
# 定义 SwiGLU 激活函数及其梯度
def swiglu(x, W1a=1.0, W1b=1.0):
return gelu(W1a * x) * (W1b * x)
def swiglu_derivative(x, W1a=1.0, W1b=1.0):
gelu_grad = gelu_derivative(W1a * x) * W1a
return gelu_grad * (W1b * x) + gelu(W1a * x) * W1b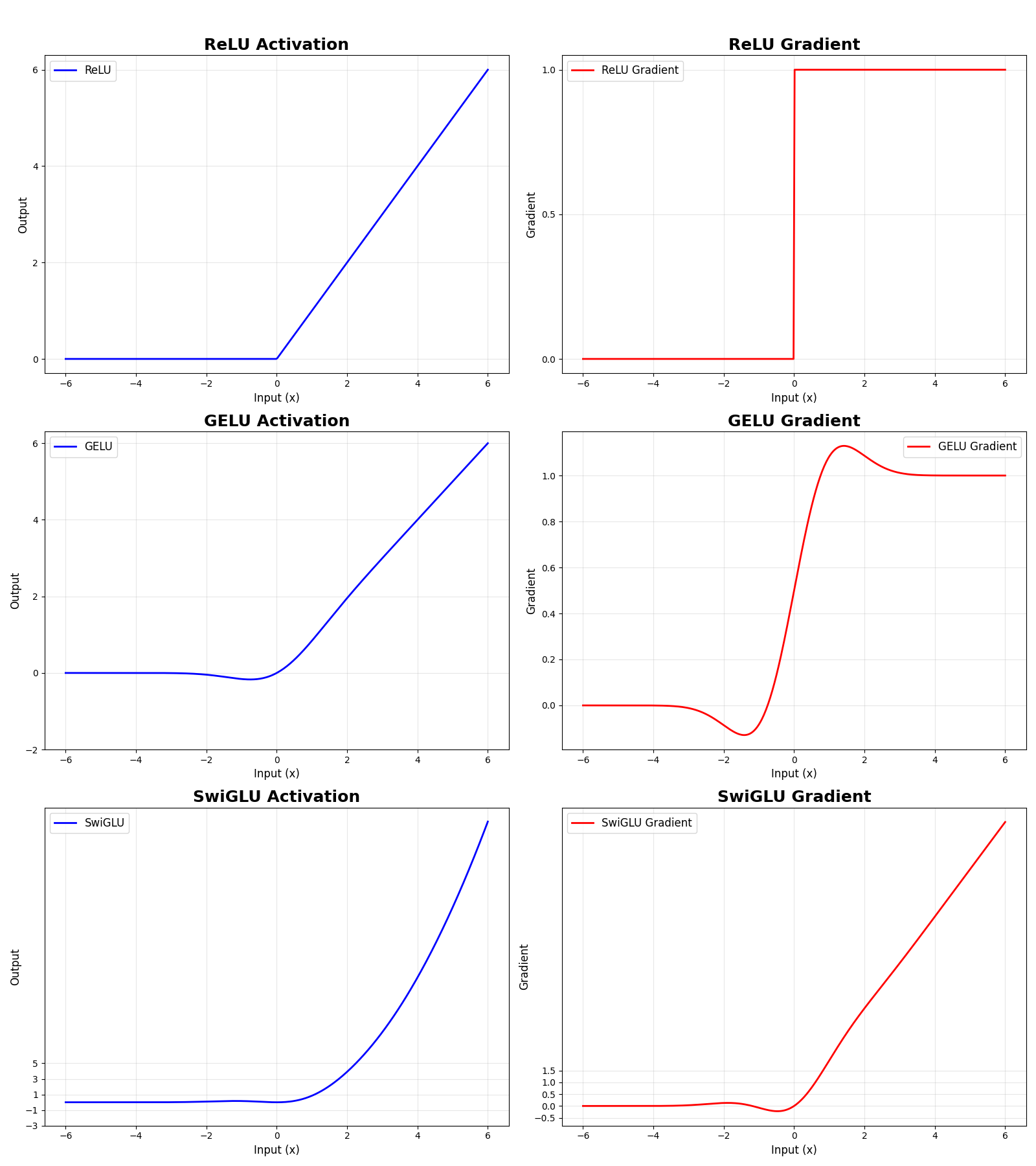
| 梯度特征 | 问题 | |
|---|---|---|
| ReLU | z>0:梯度恒为1、z≤0:梯度恒为0 | 1、死亡神经元问题,一旦输入为负值,梯度永久为0,神经元"死亡"且无法恢复;2、在0点出梯度不连续,理论上为不可导点 |
| GELU | 平滑过渡,平滑曲线没有突变点,梯度抓奸衰减但不为0 | 能够环节死亡神经元,负值区仍有小梯度,神经元可能"复活",平滑梯度有利于优化器收敛 |
| SwiGLU | 结合了门控机制导致非对称结构,梯度范围更大,梯度值可能会超过1 | 优势:能自适应调节信息流,拥有更复杂的非线性,能拟合更复杂的函数,梯度有正有负,有利于逃离局部最小值 |
- Relu适用场景:计算资源有限、深层CNN、需要稀疏激活时;
- GELU适用场景:Transformer架构(Bert、GPT)、需要稳定训练、自然语言处理;
- SwiGLU适用场景:大语言模型、追求最高性能、有充足计算资源。
5.3 SiLU激活函数
在实际实现LLaMA机构时,LLaMA官方没有适用广发好评的GELU函数,而是使用了SiLU激活函数,它是一种平滑的非线性激活函数,全称为: Sigmoid-Weighted Linear Unit。SiLU在许多深度学习任务中优于传统的激活函数,并且已经被应用于Transformer等现代架构中。
python
import numpy as np
import matplotlib.pyplot as plt
# 定义 SiLU 激活函数及其梯度
def silu(x):
return x * (1 / (1 + np.exp(-x))) # SiLU = x * sigmoid(x)
def silu_derivative(x):
sigmoid_x = 1 / (1 + np.exp(-x))
return sigmoid_x * (1 + x * (1 - sigmoid_x)) # d(SiLU)/dx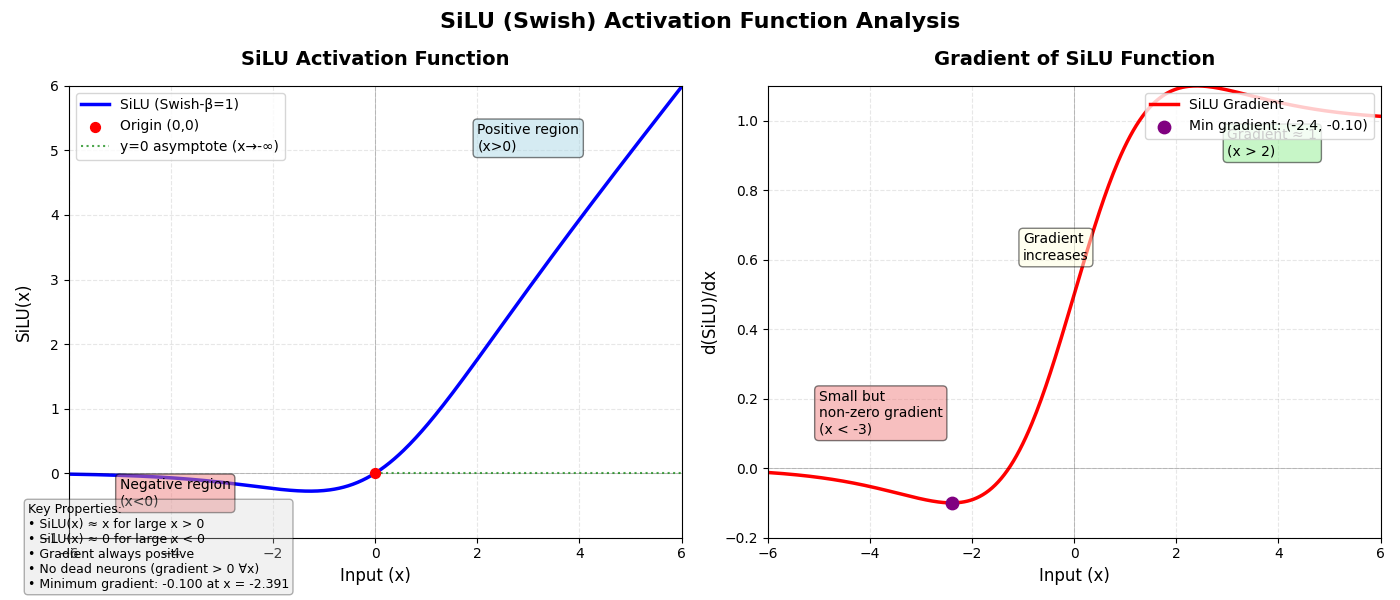
SiLU 关键特性:
- 平滑性:处处可微(包括x=0), 它在训练过程中提供了更平稳的梯度更新,使模型更容易收敛。
- 非单调梯度:梯度先减后增 。
- 无死亡神经元:梯度永不为0。
5.4 LLaMA架构的门控FFN代码
python
class FeedForward(nn.Module):
def __init__(self, dim:int, hidden_dim:int, multiple_of: int, dropout: float):
super().__init__()
if hidden_dim is None:
hidden_dim = 4* dim
#初步估算,Transformer前馈网络的传统比例(FFN维度=4*模型维度 dim=512,则hidden_dim=2048)
hidden_dim = int( 2 * hidden_dim /3)
#将维度缩小到原始的2/3,目的是减少参数数量,提高计算效率
hidden_dim = multiple_of * ((hidden_dim + multiple_of - 1) // multiple_of)
#向上取整到最近的multiple_of的倍数
#例如:(1365 + 256 - 1) // 256 = (1620) // 256 = 6
#6 * 256 = 1536 # 最终hidden_dim
# multiple_of通常是2的幂次(如256、512)
# 对齐到特定倍数可以:
# 1. 提高内存访问效率
# 2. 优化GPU计算(warp对齐)
# 3. 减少缓存未命中
self.w1 = nn.Linear(dim, hidden_dim, bias=False)
self.w2 = nn.Linear(hidden_dim, dim, bias=False)
self.w3 = nn.Linear(dim, hidden_dim, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.dropout(self.w2(F.silu(self.w1(x)) * self.w3(x))) 6. 混合专家网络用于FFN层
从门控机制出发来思考,当我们的gate不止一扇门,是否可以拥有动态的筛选策略?是否意味着我们可以同时筛选出不同、但都市场重要和精准的信息?就如果卷积神经网络利用不同的卷积核来解读不同的信息、注意力机制用不同的头来解读不同的信息一样,门控机制中我们也可以有不同的门通过不同的方式筛选信息,混合专家模型因此而诞生。
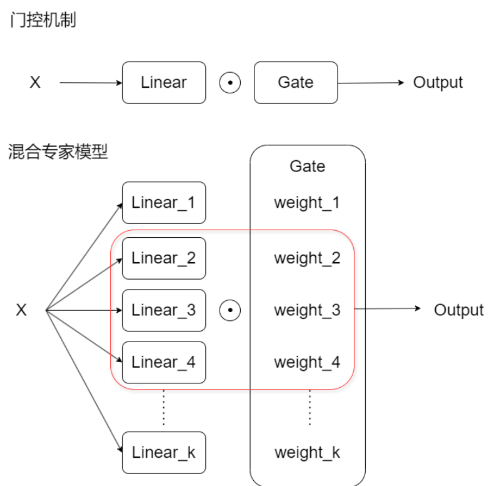
当我们使用多个们同时控制信息的流通时,这些有很多门组成的结构被称为路由器。如图所示,混合专家模型(MoE)是一种动态路由策略,通过为不同的输入选择不同的子模型(专家模型)进行计算。相比于传统的全连接前馈网络,MoE在每次向前传播时只激活部分专家模型,从而实现计算效率的提升。动态路由策略是一种在深度学习模型中使用的技术,其核心思想史:根据输入数据的特征动态选择路径或专家模型来处理信息。与传统模型估的前向传播路径不同,动态路由策略在每次向前传播时,根据输入的情况选择最合适的子网络、路径或专家来处理数据。这大幅提升了模型的灵活性、计算效率和泛化能力。
6.1 MoE原理
核心公式如下:
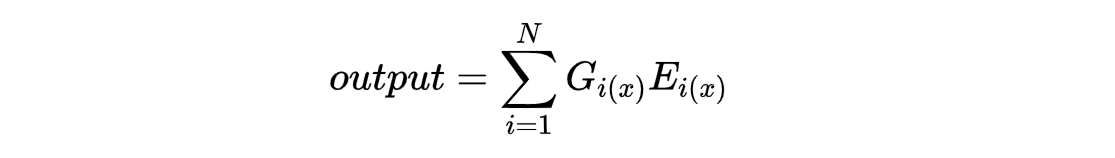
其中,Ei(x)为第i个专家模型的输出;Gi(x)为路由器(Gate)计算得到的权重,决定那些专家应该被激活以及激活的程度有多大;N表示专家模型的总量,通常来说不会采用全部的专家结果,而是采用权重最大的top-k个专家的结果,因此在实际计算中,N往往被k所替代。
重要组件:
- 专家模型(Experts): 多个全连接层或其他子模型,每个在还价处理输入的不同部分或模式。
- 路由器(Router/Gate): 为每个输入选择合适的专家(可以是一个或者多个),并未每个选中的专家分配权重。
- Sparse Activation:每次计算时,只激活少数几个专家,大幅减少计算开销。在实际计算中,路由器不会为所有专家分配非零权重,而是选择top-k个权重最高的专家激活。未被激活的专家的输出将不会参与计算,他们的权重Gi(x)会是0。
6.2 MoE与Transformer或LLaMA架构是什么关系?MoE的优势
MoE作为很好的输出模型,可以用于替代Transformer中的前馈网络(FFN)。
-
提高模型的表达能力:在传统FFN中,每一层都使用相同的参数出入所有输入,这限制了模型的表达能力。在MoE中,不同的专家网络可以学习不同的模式,每次处理输入时,可以动态选择不同的专家来增强模型的灵活性。
-
参数量高,但计算量低:使用MoE后,模型的总参数增加,但每次前向传播时,只能激活部分专家,因此计算量并不会线性增加。
-
增强泛化能力:每个专家专注于学习特定模式,有助于减少模型的过拟合,提高模型的泛化能力。
6.3 MoE训练流程
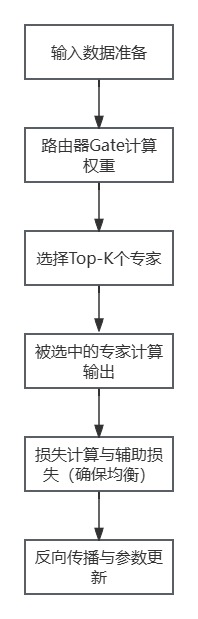
在混合专家模型(MoE)中,由于其稀疏激活机制,专家的选择并非针对整个批次的整体输出,而是针对每个token进行选择和计算的,这就是为什么一个专家的激活频率是基于每个token来统计的。在引入MoE后,模型会为每个token或每个实践部单独计算路由器输出,从而决定该token应该选择哪些专家。这意味着:每个token的计算会激活不同的专家,每个专家在同一个批次不同的token上可能会被多次激活。
少数专家瓶颈是MoE常见的问题之一,在实际的训练中可能会出现以下几种情况:
1、专家的偏向性:由于路由器的训练偏差,某些专家会被频繁激活,而其他专家几乎不被使用;
2、激活不均衡:一些专家会承担大部分计算,而其他专家却被"闲置",无法获得足够的训练机会;
3、参数更新不充分:未被激活的专家参数得不到更新,导致这些专家无法在模型训练中发挥作用。
为了解决专家瓶颈问题,通常会引入"辅助损失(Auxiliary Loss)"机制,用来均衡专家的使用频率,确保所有专家能在训练中获得足够的激活机会。这种辅助损失会被叠加在神经网络的主要损失(交叉熵损失/MSE)上,它在训练过程中与主要损失一起影响模型的反向传播和参数更新。这种设计确保模型在优化主要任务时,也能实现额外的目标:均衡专家的使用频率、提高模型的泛化能力。Total Loss = MainLoss + alpha * Auxiliary Loss,其中alpha是用来控制平衡的超参数。
在Mixture of Experts (MoE)模型中,常见的辅助损失用于帮助训练过程中的专家选择更加平衡,防止某些专家过渡选择或者其他专家很少被选中。以下是常见MoE辅助损失的例子:
负载平衡损失 (Load Balancing Loss):促进不同专家的负载更加平衡,避免过度依赖某个专家。一种常见的形式是使用专家的选择频率与分配的均衡性来构造。通常,目标是让每个专家的选择概率与理想的均匀分布更接近。
基于熵的损失 (Entropy-based Loss):通过增加专家选择的熵,鼓励模型选择更多的专家来参与计算,从而减少某些专家的过载。
KL 散度损失 (KL Divergence Loss):将实际的专家选择分布与理想的均匀分布进行比较。
专家负载正则化 (Expert Load Regularization):控制每个专家的负载,使得负载接近于模型的理想目标负载,比如让每个专家处理相同数量的样本。
实际使用的损失函数:在进行实践时,我们可以使用平均权重和平均使用率来平衡专家的选择。比如说:
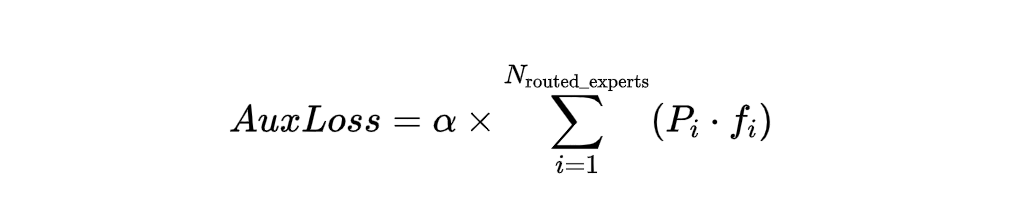
N routed_experts是专家的数量;
Pi是所有专家的平均权重;
fi是专家的平均使用率。
python
import numpy as np
#定义三个权重矩阵和对应的top-k矩阵
#非常均衡,但是每个专家对每个token的处理高度类似
weight_1 = np.array([
[0.34, 0.34, 0.32],
[0.34, 0.32, 0.34],
[0.34, 0.34, 0.32],
[0.32, 0.34, 0.34]
])
#二维矩阵,每一行是针对每一个token的每个专家的权重值
topk_1 = np.array([
[1, 1, 0],
[1, 0, 1],
[1, 1, 0],
[0, 1, 1]
])
#针对wight1来说,选择权重值最高的前两个专家
#每个专家都又被用到,也实现了一定的特异化
weight_2 = np.array([
[0.6, 0.25, 0.15],
[0.4, 0.4, 0.2],
[0.3, 0.6, 0.1],
[0.04, 0.06, 0.9]
])
topk_2 = np.array([
[1, 1, 0],
[1, 1, 0],
[1, 1, 0],
[0, 1, 1]
])
# 不均衡,只有专家1和专家2被使用
weight_3 = np.array([
[0.6, 0.25, 0.15],
[0.4, 0.4, 0.2],
[0.3, 0.6, 0.1],
[0.9, 0.06, 0.04]
])
print(weight_3.mean(axis=0))
topk_3 = np.array([
[1, 1, 0],
[1, 1, 0],
[1, 1, 0],
[1, 1, 0]
])
print(topk_3.mean(axis=0))
#定义计算pi和fi的函数
def calculate_aux_loss(weights, topk):
pi = weights.mean(axis=0) #计算纵向均值pi:每个专家被激活的概率
fi = topk.mean(axis=0) #计算纵向值fi,每个专家被使用的频率
pi_fi = pi * fi #计算pi * fi
return pi_fi.sum() #返回aux_loss损失
#计算三个aux_loss
aux_loss_1 = calculate_aux_loss(weight_1, topk_1)
aux_loss_2 = calculate_aux_loss(weight_2, topk_2)
aux_loss_3 = calculate_aux_loss(weight_3, topk_3)
print(aux_loss_1, aux_loss_2, aux_loss_3)因此可以得出结论,当专家使用频率越不均衡时,辅助损失越大。
python
import torch
import torch.nn.functional as F
bsz = 3
seq_len = 10
total_tokens = bsz * seq_len #一共有300个单词
#从所有专家那里获得的输出结果
hidden_states = torch.randn(size=(30, 512))
#Token 1 的隐藏状态: (512维)
#权重的初始化参数
self_weight = torch.randn(size=(6, 512))
#专家1的权重: (512维)
#利用线性层将二者相连,构建每个token上每个专家的权重
weights = F.linear(hidden_states, self_weight, None)
#等价于(30, 512) @ (512, 6) ,Linear内部做了设计,可以直接点积
print(weights.shape) #每个token在每个专家上的得分
#torch.Size([30, 6])最终得到了每个token的所有6个专家的得分6.4 MoE训练阶段和推理阶段的不同
在推理阶段,不需要存储所有专家的梯度,只激活选中的专家。
| 阶段 | 训练 | 推理 |
|---|---|---|
| 激活专家 | Tok-k专家参与计算,但所有专家更新梯度 | 只激活tok-k专家,其他专家不计算 |
| 反向传播 | 需要反向传播和梯度计算 | 不需要梯度计算 |
| 内存占用 | 高(需存储所有专家的参数和梯度) | 低(只需要存储部分专家的输出) |
| 计算量 | 高 | 低 |
| 负载均衡 | 需要负载均衡,避免专家使用不均 | 不需要,因为只需要一次向前传播 |
| 跨设备通信 | 需频繁跨设备通信 | 通信需求较低 |
6.5 MoE模型代码
python
# ============ MoEGate 类 ============
class MoEGate(nn.Module):
def __init__(self, config: LMConfig):
super().__init__()
self.config = config
self.top_k = config.num_experts_per_tok
self.n_routed_experts = config.n_routed_experts
self.scoring_func = config.scoring_func
self.alpha = config.aux_loss_alpha
self.seq_aux = config.seq_aux
self.norm_topk_prob = config.norm_topk_prob
self.gating_dim = config.dim
self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))
self.reset_parameters()
def reset_parameters(self):
nn.init.kaiming_uniform_(self.weight, a=math.sqrt(5))
def forward(self, hidden_states):
bsz, seq_len, h = hidden_states.shape
hidden_states = hidden_states.view(-1, h)
# 计算专家得分
logits = F.linear(hidden_states, self.weight, None)
if self.scoring_func == 'softmax':
scores = logits.softmax(dim=-1)
else:
raise NotImplementedError(f'不支持的scoring_func: {self.scoring_func}')
# 选择top-k专家
topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)
if self.top_k > 1 and self.norm_topk_prob:
denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20
topk_weight = topk_weight / denominator
# 辅助损失
if self.training and self.alpha > 0.0:
scores_for_aux = scores
aux_topk = self.top_k
topk_idx_for_aux_loss = topk_idx.view(bsz, -1)
if self.seq_aux:
scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)
ce = torch.zeros(bsz, self.n_routed_experts, device=hidden_states.device)
ce.scatter_add_(
1, topk_idx_for_aux_loss,
torch.ones(bsz, seq_len * aux_topk, device=hidden_states.device)
).div_(seq_len * aux_topk / self.n_routed_experts)
aux_loss = (ce * scores_for_seq_aux.mean(dim=1)).sum(dim=1).mean() * self.alpha
else:
mask_ce = F.one_hot(topk_idx_for_aux_loss.view(-1), num_classes=self.n_routed_experts)
ce = mask_ce.float().mean(0)
Pi = scores_for_aux.mean(0)
fi = ce * self.n_routed_experts
aux_loss = (Pi * fi).sum() * self.alpha
else:
aux_loss = None
return topk_idx, topk_weight, aux_lossMoEGate主要做了三件事:1、计算每个专家的权重;2、挑选前top-k个专家;3、计算辅助损失函数。其核心代码是:
python
# 1. 计算每个专家的权重(得分)
scores = F.linear(hidden_states, self.weight).softmax(dim=-1)
# 输出: (num_tokens, num_experts)
# 意义: 每个token对每个专家的"偏好程度"
# 2. 挑选前top-k个专家
topk_weight, topk_idx = torch.topk(scores, k=self.top_k)
# topk_idx: 选中的专家编号 (num_tokens, top_k)
# topk_weight: 对应的权重 (num_tokens, top_k)
# 3. 计算辅助损失函数
aux_loss = 计算负载均衡损失() # 防止专家使用不均
# 只在训练时计算,推理时不用整体的文件有三个:分别是config.py、moe-gate.py、moe_layer.py
python
# ============ 配置类 ============
from dataclasses import dataclass
from typing import Optional
@dataclass
class LMConfig:
"""语言模型配置类"""
# 模型基本参数
dim: int = 512
n_layers: int = 12
vocab_size: int = 50257
# MoE门控参数
n_routed_experts: int = 8
num_experts_per_tok: int = 2
# 门控计算参数
scoring_func: str = 'softmax'
norm_topk_prob: bool = True
aux_loss_alpha: float = 0.01
seq_aux: bool = False
# 专家网络参数
expert_dim: Optional[int] = None
expert_intermediate_size: int = 2048
expert_activation: str = 'gelu'
def __post_init__(self):
if self.expert_dim is None:
self.expert_dim = self.dim
python
from config import LMConfig
import torch.nn as nn
import torch
import math
import torch.nn.functional as F
# ============ MoEGate 类 ============
class MoEGate(nn.Module):
def __init__(self, config: LMConfig):
super().__init__()
self.config = config
self.top_k = config.num_experts_per_tok
self.n_routed_experts = config.n_routed_experts
self.scoring_func = config.scoring_func
self.alpha = config.aux_loss_alpha
self.seq_aux = config.seq_aux
self.norm_topk_prob = config.norm_topk_prob
self.gating_dim = config.dim
self.weight = nn.Parameter(torch.empty((self.n_routed_experts, self.gating_dim)))
self.reset_parameters()
def reset_parameters(self):
nn.init.kaiming_uniform_(self.weight, a=math.sqrt(5))
def forward(self, hidden_states):
bsz, seq_len, h = hidden_states.shape
hidden_states = hidden_states.view(-1, h)
# 计算专家得分
logits = F.linear(hidden_states, self.weight, None)
if self.scoring_func == 'softmax':
scores = logits.softmax(dim=-1)
else:
raise NotImplementedError(f'不支持的scoring_func: {self.scoring_func}')
# 选择top-k专家
topk_weight, topk_idx = torch.topk(scores, k=self.top_k, dim=-1, sorted=False)
if self.top_k > 1 and self.norm_topk_prob:
denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20
topk_weight = topk_weight / denominator
# 辅助损失
if self.training and self.alpha > 0.0:
scores_for_aux = scores
aux_topk = self.top_k
topk_idx_for_aux_loss = topk_idx.view(bsz, -1)
if self.seq_aux:
scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)
ce = torch.zeros(bsz, self.n_routed_experts, device=hidden_states.device)
ce.scatter_add_(
1, topk_idx_for_aux_loss,
torch.ones(bsz, seq_len * aux_topk, device=hidden_states.device)
).div_(seq_len * aux_topk / self.n_routed_experts)
aux_loss = (ce * scores_for_seq_aux.mean(dim=1)).sum(dim=1).mean() * self.alpha
else:
mask_ce = F.one_hot(topk_idx_for_aux_loss.view(-1), num_classes=self.n_routed_experts)
ce = mask_ce.float().mean(0)
Pi = scores_for_aux.mean(0)
fi = ce * self.n_routed_experts
aux_loss = (Pi * fi).sum() * self.alpha
else:
aux_loss = None
return topk_idx, topk_weight, aux_lossmoe_layer.py
python
import torch
import torch.nn as nn
from config import LMConfig
from moe_gate import MoEGate
# ============ Expert 类 ============
class Expert(nn.Module):
"""单个专家网络"""
def __init__(self, config):
super().__init__()
self.config = config
self.fc1 = nn.Linear(config.dim, config.expert_intermediate_size)
self.fc2 = nn.Linear(config.expert_intermediate_size, config.dim)
self.activation = nn.GELU() if config.expert_activation == 'gelu' else nn.ReLU()
self.dropout = nn.Dropout(0.1) # 简化,实际从config读取
def forward(self, x):
return self.fc2(self.dropout(self.activation(self.fc1(x))))
# ============ MoELayer 类 ============
class MoELayer(nn.Module):
"""完整的MoE层"""
def __init__(self, config):
super().__init__()
self.config = config
self.gate = MoEGate(config) # 这里使用上面定义的MoEGate
self.experts = nn.ModuleList([
Expert(config) for _ in range(config.n_routed_experts)
])
def forward(self, x):
# 1. 门控计算:选择专家
indices, weights, aux_loss = self.gate(x)
# 2. 展平输入
x_flat = x.view(-1, x.shape[-1])
# 3. 初始化输出
output = torch.zeros_like(x_flat)
# 4. 处理每个专家
for i, expert in enumerate(self.experts):
# 获取需要当前专家处理的token
mask = (indices == i).any(dim=-1) # (batch*seq,)
if mask.any():
expert_input = x_flat[mask]
expert_output = expert(expert_input)
# 获取这些token在当前专家上的权重
expert_weights = weights[mask].sum(dim=-1, keepdim=True)
# 累加到输出
output[mask] += expert_output * expert_weights
# 5. 恢复形状并返回
output = output.view_as(x)
return output, aux_loss使用示例
python
# ============ 使用示例 ============
if __name__ == "__main__":
# 创建配置
config = LMConfig(dim=512, n_routed_experts=8, num_experts_per_tok=2)
# 创建MoE层
moe_layer = MoELayer(config)
# 模拟输入
x = torch.randn(4, 32, 512)
# 前向传播
moe_layer.train() # 设置为训练模式,会计算辅助损失
output, aux_loss = moe_layer(x)
print(f"输入形状: {x.shape}")
print(f"输出形状: {output.shape}") # (4, 32, 512)
print(f"辅助损失: {aux_loss.item():.6f}" if aux_loss输入形状: torch.Size([4, 32, 512])
输出形状: torch.Size([4, 32, 512])
辅助损失: 0.010112