作为一个刚刚进入博0的学生,发现虽然本科就是通信但是基础知识还有很多不牢固的地方,如果有任何说的不对的地方敬请大家指正,在讨论中进步。

3.1 瑞利衰落信道中的检测
3.1.1非相干检测
书中主要先讨论衰落信道中非常简单的检测问题,采用如下平坦衰落模型,信道可以用单个离散时间复滤波器抽头表示,并且简写为
:
其中,同时假定为瑞利衰落,
,方差被归一化为1。暂时不去规定不同时刻
衰落系数
的相关性,也不对接收机关于
的先验知识做出任何假设。(这个假设是一个非相干通信的假设)
考虑幅度为的未编码二进制对极信号传输(即二进制相移键控BPSK),即
,并且这个码元是关于时间相互独立。无论发射的是
还是
,由于
在前序设定成了复高斯随机变量
,其具有旋转不变性,那么其可s以写成
,并且
,和
是独立的。在没有噪声的情况下,接收信号
的相位在0到
上是均匀分布的,这种信号的传输方案是完全失败的**(针对为什么完全失败,在这里我们可以理解成,在发射a和-a的时候,没有噪声的话我们在接收端可以看到
和
,由于
和
是完全随机的,两者的统计分布是一模一样的,并且发送-a和+a的时候
都是不一样的,所以相位部分其实是没办法辨别这两个信号的,从幅度来看很明显两个都一样根本无法区分------这里如果有问题或者大家有更合适的想法真的很希望大家可以留下宝贵的评论)**。
此处,接收幅度与发射码元无关,而二进制对极信号传输是二进制调制,相位调制一般会存在如上的缺陷,所以在这里需要的信号结构应该是,不同的信号具有不同的幅度或者对码元进行编码(可以认为是让多个码元之间存在一些相对关系)。
因此开始考虑正交信号传输(可以被认为是码元编码的一种特殊的类型),考虑的正交调制是简单的正交调制,就是binary pulse-position modulation(二进制脉冲调制),对于一对时间样本A、B来说,发送的如下所示:
因此,进行信号检测的依据是接收到的信号:
这里根据最大似然比准则:
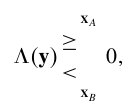
进行具体的判决,构造如下的似然比:
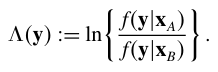
如果发送的是,则有
,并且
与
相互独立。如果发送的是
,择有
,并且
与
相互独立,因此联合PDF可以写成乘积的形式:
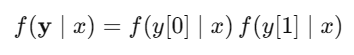
从而分别写出发射和
假设下的联合PDF:
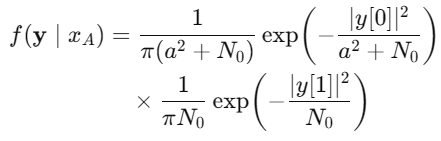
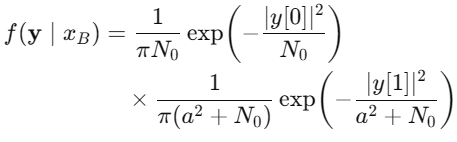
公共常数相同,直接抵消,剩下指数项:
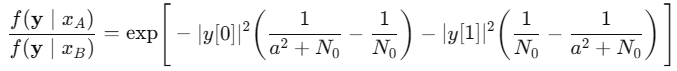
取了对数以后:
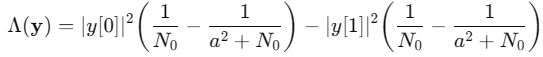
因此可以利用下式计算对数似然比:
最佳判决准则为:如果,则判决发射信号为
,否则发射信号就是
。这一准则没有利用接收信号的相位,因为信道增益的随机位置相位(还是有可能存在一些轻微的波动-这里如果有友友可以更好的解释希望可以留下你宝贵的评论呀)会导致相位对检测没有任何用处。
从几何上来看,检测器的功能可以解释为将接收矢量y投影到两个可能的发射矢量和
上,冰比较两个投影的能量:
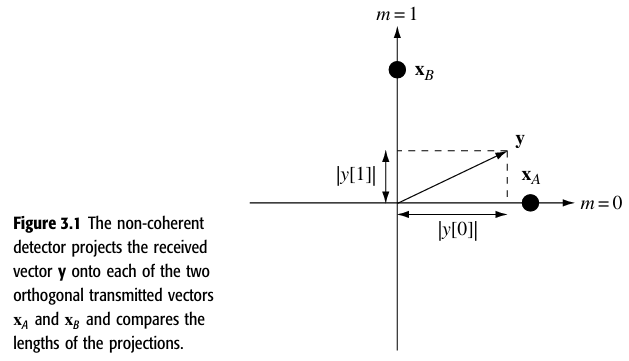
因此,这种检测器也被称为能量检测器或平方律检测器,然而最佳检测器并不依赖于与
的相关性。
接下来可以分析出该检测器的差错概率:由对称性假定发射信号,在该假设条件下
与
是方差分别为
与
的相互独立的循环对称复高斯随机变量,根据附录可知,
与
是服从均值分别为
与
的指数分布。于是,可以通过直接积分来算出差错概率:
针对上述式子,证明如下:
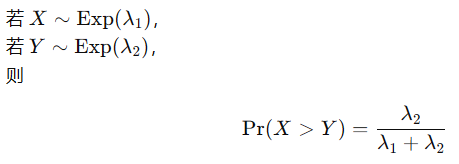
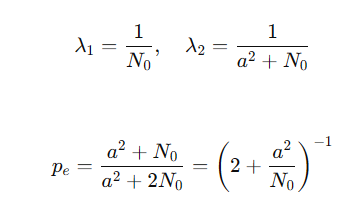
而信噪比的一般定义为:


对于每个复数码元时间内的噪声能量我们都将其定义为(因为在此处讨论的正交调制方法仅仅采用了实码元,因此仅在同相支路(I)上传输,从直觉上来看每个实码元的噪声能量
来定义信噪比会更清晰,后续章节存在同时在I和Q两个支路上传输的情况) ,对于正交调制方案而言,每个码元时间内的平均接收能量为
,因此有
,因此带入公式3.9就可以得到:
根据上述的推导 ,如果希望得到,就需要达到大概
的信噪比,更加可靠的通信就会需要更大的发射功率。
3.1.2 相干检测
由于非相干最大似然接收机在衰落信道中的性能较差,开展这种情况下性能与无衰落AWGN信道下的检测性能进行比较:
对于极信号传输(BPSK)而言,,充分统计量为
,根据前面的分析,其实这里的判决不需要看相位了,只需要看实部,虚部只有噪声,ML主要还是根据实部来评判,同时,此时的差错概率为:
差错概率是如何得到的呢:

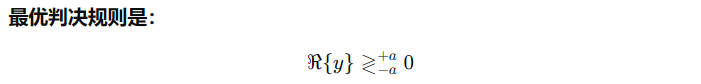
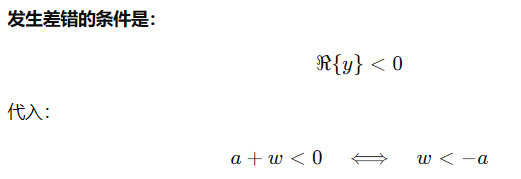
所以差错本质上是: 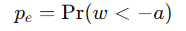 ,并且此时有
,并且此时有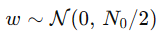 ,那么上述问题就可以变化为**"高斯随机变量落到某个阈值之下"的概率问题**,而上述的公式表示的是一个Q函数,这里给出Q函数的定义:
,那么上述问题就可以变化为**"高斯随机变量落到某个阈值之下"的概率问题**,而上述的公式表示的是一个Q函数,这里给出Q函数的定义: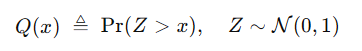
在计算Q函数之前需要标准化噪声,定义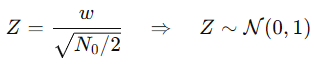 ,那么差错事件就会变成:
,那么差错事件就会变成: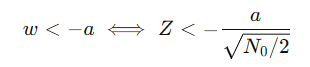 ,利用高斯对称性可以得到:
,利用高斯对称性可以得到:
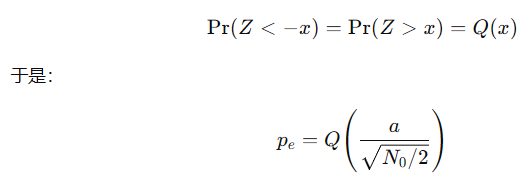
证明完毕。
式子当中的SNR我们已经在上一节证明了,Q函数为N(0,1)随机变量的互补累积分布函数,该函数随指数衰减:
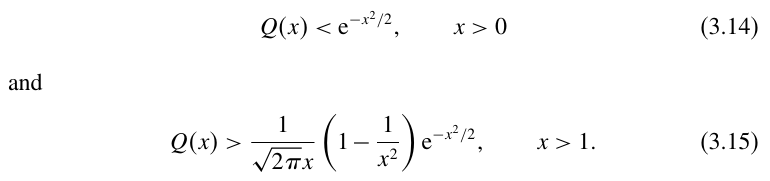
因此,检测差错概率在AWGN信道中是随着信噪比指数衰减的,而在衰落信道中仅仅随着信噪比的倒数衰减的。
AWGN信道中是随着信噪比指数衰减的:
因为,我们可以把
代入3.15可以得到
,证毕。
同样为了获得的差错概率,AWGN信道所需的信噪比只需要是7dB。在这里需要注意
是两个星座点之间的间隔,是高斯噪声标准偏差的整数倍,上述观察结果可以表明,当该间隔远大于1的时候,差错概率会非常小。
当该间隔远大于1的时候,差错概率会非常小:指的是信号之间的间隔已经明显大于噪声的抖动幅度了 **。**如果这个值大于1,从数学的角度来看:
 当星座点之间的间隔已经是噪声标准差的很多倍时,噪声必须出现远超标准差的极端偏移才能造成跨界判错,这已经是一种高斯尾部事件,概率指数级别的小
当星座点之间的间隔已经是噪声标准差的很多倍时,噪声必须出现远超标准差的极端偏移才能造成跨界判错,这已经是一种高斯尾部事件,概率指数级别的小
未完待续-如果有希望我更新的友友可以留下评论哈哈哈,一起努力一起进步