冯·诺依曼体系结构下,计算单元与存储层级之间存在显著的速度鸿沟:现代 CPU 的单核主频可达 3--5 GHz,L1 缓存访问延迟约 1 纳秒,而主内存(DRAM)延迟通常在 70--100 纳秒,SSD 的随机读写则高达数十微秒------比 L1 缓存慢了近十万倍。这种速度断层意味着,一旦计算流程频繁陷入对低速存储的等待,整个系统就会从 compute-bound 转为 memory-bound:CPU 的算力无法被充分利用,因为数据"跟不上"指令的需求。
compute-bound:计算跟不上数据传输能力
memory-bound:数据传输跟不上计算能力
典型的例子是传统的 I/O 模型。每次调用 read 或 write 操作一个文件描述符,都会触发一次系统调用,内核需从用户态切换到内核态,再通过页缓存或直接 I/O 访问磁盘。若用 accept + read/write + send 处理网络连接,每个连接独占一个线程或进程,那么成千上万个并发连接将导致大量上下文切换、系统调用和零散的内存拷贝。这些操作本身不复杂,但因粒度太细、频率太高,使得 CPU 大量时间花在等待网卡 DMA 完成或内核缓冲区同步上,而非是真正处理业务逻辑------这是 memory-bound 的典型表现。
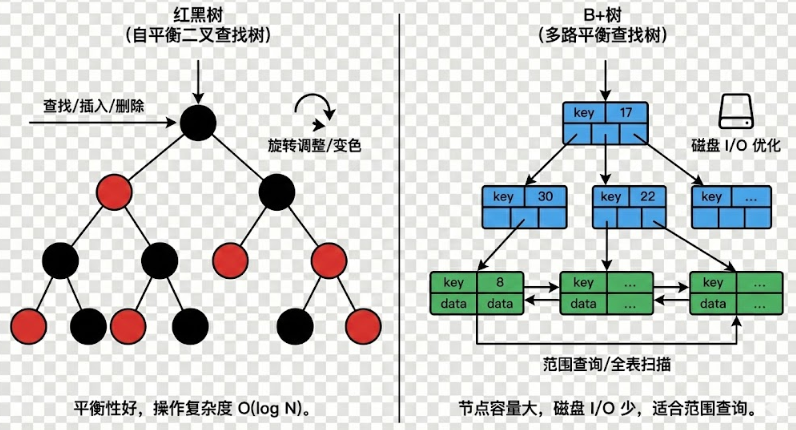
另一个场景是使用红黑树或普通二叉搜索树存储海量键值对。当数据规模超出内存容量,树节点不得不换出到磁盘。此时,树的高度(O(log n))虽看似合理,但每下降一层都可能触发一次磁盘 I/O。对于十亿级数据,log₂(10⁹) ≈ 30,意味着一次查找可能引发 30 次磁盘访问。而磁盘的随机 I/O 吞吐极低,延迟极高,整个查询过程几乎完全被 I/O 阻塞。即便数据全在内存中,若节点分散分配,缓存行利用率也会极差,进一步加剧 memory-bound。
这些问题的根源在于**:离散、高频、小粒度的操作放大了存储层级间的性能差距。** 解决方案往往指向同一种思路,批处理(batching)
I/O 多路复用(如 epoll)允许单个线程同时监听成千上万个文件描述符,仅在有事件就绪时才批量返回可操作的 fd 列表。这样,系统调用次数从 O(n) 降至 O(1)(均摊),上下文切换和内核-用户空间拷贝大幅减少,CPU 得以集中处理有效数据。
B+ 树放弃二叉树的"瘦高"结构,转而采用"矮胖"形态:每个内部节点容纳大量键(例如 100+),从而将树高压缩至 2--4 层。更重要的是,叶子节点被组织成有序链表,并按页(如 4KB 或更大)连续存储。这样,一次磁盘 I/O 可读取整页数据,包含数十甚至上百个键值对,极大提升 I/O 效率。即使数据在磁盘上,也能通过局部性原理将多次潜在 I/O 合并为一次------本质上,是以更大的单次操作换取更少的总操作次数。
无论是 I/O 多路复用还是 B+ 树,其核心都不是发明新算法,而是重新组织操作的粒度与节奏,将原本零散、随机、高频的访问,聚合成稀疏、顺序、批量的请求,来解决这个 memory-bound 的问题。