P6648 [CCC 2019] Triangle: The Data Structure
时间限制: 2.00s 内存限制: 128.00MB
复制 Markdown 退出 IDE 模式
题目背景
在 Shuchong 的平行宇宙里,计算机学中的最重要的数据结构就是三角形。
注:因为原数据包太大,故这题缩减了一些数据,具体缩减的数据点如下:
- Subtask 1:1 ~ 10
- Subtask 2:1 ~ 10
所以此题拥有的测试点为:
- Subtask 1:11 ~ 26
- Subtask 2:11 ~ 24
若想测试本题没有的测试点请到 此处 测试。
题目描述
大小为 m 的一个三角形由 m 行组成,第 i 行包含 i 个元素。
并且,这些行必须排为等边三角形的形状。
比如说,以下是一个 m=4 的三角形。
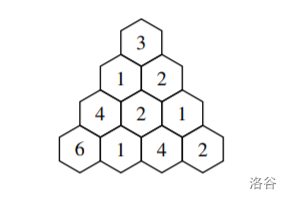
每个三角形还包含子三角形。
比如说上面这个三角形,包含:
- 10 个大小为 1 的三角形。
- 6 个大小为 2 的三角形。
- 3 个大小为 3 的三角形。
注意,每个三角形都是自身的子三角形。
现在给定一个大小为 n 的三角形,求对于每个大小为 k 的子三角形,子三角形内几个数的最大值的和。
输入格式
第一行两个整数 n,k 代表三角形的大小和要求的子三角形的大小。
接下来 n 行第 i 行有 i 个整数代表这个三角形。
输出格式
一行一个整数代表对于每个大小为 k 的子三角形,子三角形内几个数的最大值的和。
输入输出样例
输入 #1复制运行
4 2
3
1 2
4 2 1
6 1 4 2输出 #1复制运行
23说明/提示
数据规模与约定
- Subtask 1(25 pts):n≤1000。
- Subtask 2(75 pts):无特殊限制。
对于 100% 的数据,1≤k≤n≤3000,0≤ 三角形内每个数 ≤109。
说明
翻译自 CCC 2019 Senior T5 Triangle: The Data Structure。
翻译者:@一只书虫仔。
题目要求我们求每个大小为k的三角形的最大值 之和 对于最值问题 有明显的区间可重复性 可以考虑st表解决
对于一个2^k 的三角形 我们可以用最多六个2^k-1 的三角形进行覆盖 得出最大值
同时防止内存 加上滚动数组
对于询问部分 我们要从边界开始减 防止越界 然后计算合适的偏移量 计算中间的小三角形 最后累加答案即可
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=3e3+5;
int st[N][N][2],n,k;
long long ans;
int query(int i,int j){
int t=log2(k);
int v=t&1;
int l=i+k-1,r=j+k-1;
int res=max(st[i][j][v],max(st[l-(1<<t)+1][j][v],st[l-(1<<t)+1][r-(1<<t)+1][v]));
if(t<=1)return res;
int dis=(k-(1<<t))>>1;
res=max(max(res,st[l-(1<<t)+1][j+dis][v]),max(st[i+dis][j][v],st[i+dis][j+dis][v]));
return res;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>k;
int len=log2(k);
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>st[i][j][0];
}
}
for(int t=1;t<=len;t++){
int u=t&1,v=u^1;
for(int i=1;i<=n-(1<<t)+1;i++){
for(int j=1;j<=i;j++){
st[i][j][u]=max(st[i][j][v],max(st[i+(1<<t-1)][j][v],st[i+(1<<t-1)][j+(1<<t-1)][v]));
if(t>1){
st[i][j][u]=max(st[i][j][u],max(st[i+(1<<(t-1))][j+(1<<t-2)][v],max(st[i+(1<<t-2)][j+(1<<t-2)][v],st[i+(1<<t-2)][j][v])));
}
}
}
}
for(int i=1;i<=n-k+1;i++){
for(int j=1;j<=i;j++){
ans+=query(i,j);
}
}
cout<<ans<<'\n';
return 0;
}