面试常问系列(一)-激活函数-relu/leaky_relu/prelu/dice

flying_13142026-01-18 15:10

目录

一、为什么会出现这些激活函数

一、梯度消失问题的根源

[1. Sigmoid/Tanh 的梯度消失](#1. Sigmoid/Tanh 的梯度消失)

Sigmoid：

Tanh：

[2. 梯度消失的连锁反应](#2. 梯度消失的连锁反应)

[二、ReLU、Leaky ReLU 和 PReLU 的解决方案](#二、ReLU、Leaky ReLU 和 PReLU 的解决方案)

[1. ReLU：直接截断负区间](#1. ReLU：直接截断负区间)

[2. Leaky ReLU：为负区间赋予微小梯度](#2. Leaky ReLU：为负区间赋予微小梯度)

[3. PReLU：自适应学习负区间梯度](#3. PReLU：自适应学习负区间梯度)

三、对比总结

四、关键结论

二、进一步延伸PReLU

[一、PReLU 的核心机制：通道级可学习 α](#一、PReLU 的核心机制：通道级可学习 α)

[1. α 的学习方式](#1. α 的学习方式)

[2. α 如何与特征关联？](#2. α 如何与特征关联？)

[二、为什么 PReLU 能区分不同特征的重要性？](#二、为什么 PReLU 能区分不同特征的重要性？)

[1. 特征分布差异的直观解释](#1. 特征分布差异的直观解释)

[2. PReLU 的自适应调整过程](#2. PReLU 的自适应调整过程)

[三、与 Leaky ReLU 的对比：固定 α 的局限性](#三、与 Leaky ReLU 的对比：固定 α 的局限性)

[四、实际代码示例（PyTorch 实现）](#四、实际代码示例（PyTorch 实现）)

五、总结

三、Dice

一、PReLU的作用与局限性

[1. PReLU的原理](#1. PReLU的原理)

[2. PReLU的局限性](#2. PReLU的局限性)

二、Dice的改进：数据驱动的自适应激活

Dice的优势

三、DIN中替换PReLU为Dice的动机

五、总结

一、为什么会出现这些激活函数

大家有时间的话，可以看一下这篇文章，描述比较详细：

面试常问系列(一)-神经网络参数初始化

我这里不做过多深入讲解，简单描述下：

ReLU、Leaky ReLU 和 PReLU 确实是为了解决传统激活函数（如 Sigmoid 和 Tanh）的梯度消失问题 而提出的。它们的解决方案核心在于调整负区间的梯度行为，避免深层网络中梯度逐层衰减至零。以下从原理、数学推导和具体例子三方面详细说明它们如何解决梯度消失问题。

一、梯度消失问题的根源

1. Sigmoid/Tanh 的梯度消失

Sigmoid：

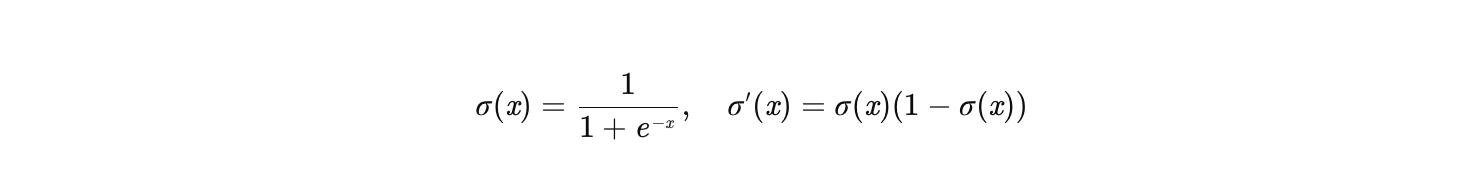
  • 输出范围：(0, 1)，梯度最大值为 0.25（当 x=0 时）。

  • 问题：在深层网络中，梯度通过链式法则逐层相乘，多次乘以 0.25 会导致梯度指数级衰减（如 0.25^10≈10−6），使得底层参数几乎无法更新。

Tanh：
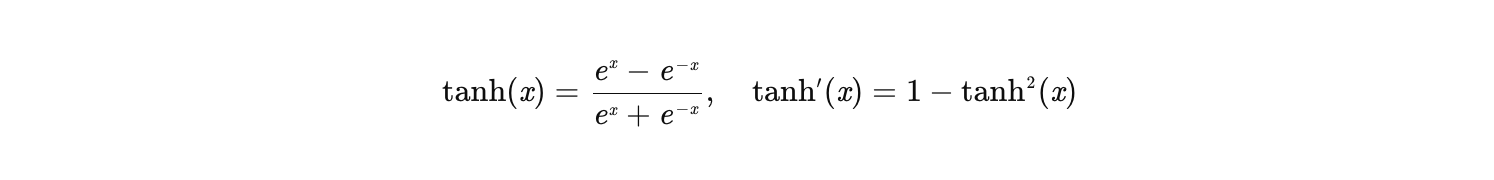
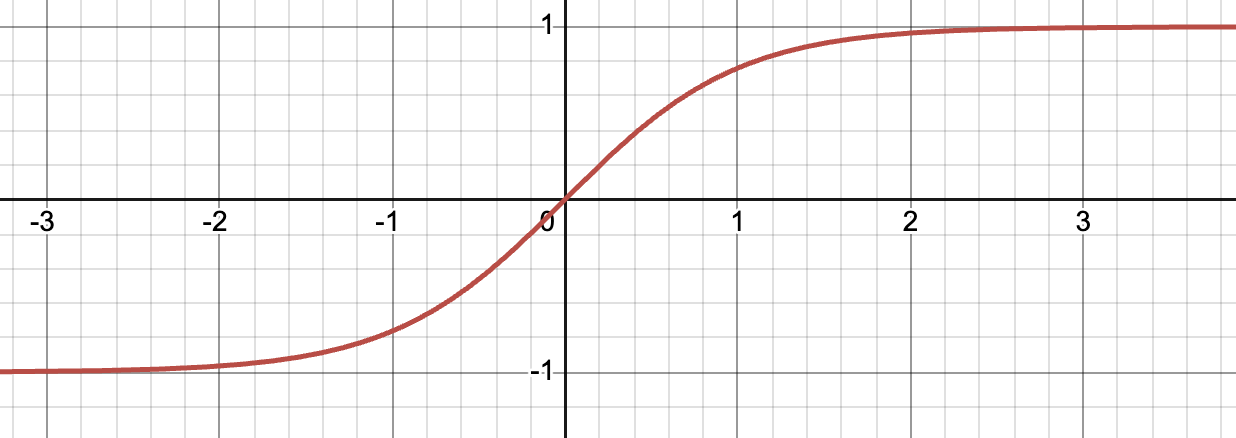
  • 输出范围：(-1, 1)，梯度最大值为 1（当 x=0 时）。
  • 问题：虽然梯度最大值比 Sigmoid 大，但在远离零点的区域（如 ∣x∣>3），梯度仍会趋近于 0，导致梯度消失。

2. 梯度消失的连锁反应

在反向传播中，梯度更新公式为：

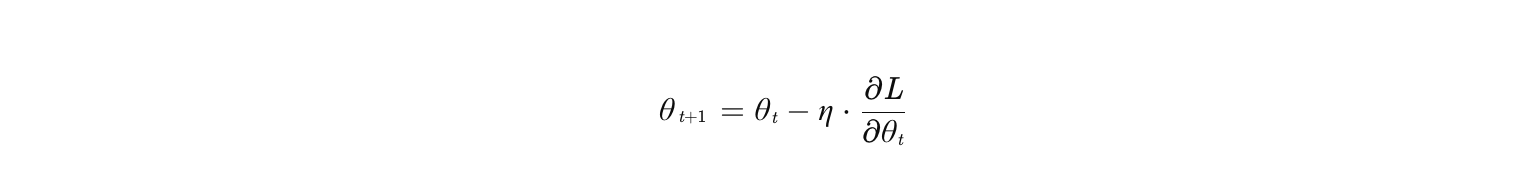
其中 是通过链式法则计算的梯度：

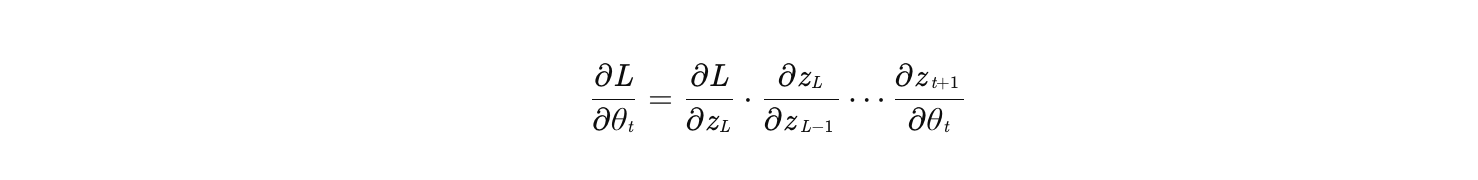
若中间某层的激活函数梯度 接近 0，整个梯度会迅速衰减，导致底层参数无法更新（即"梯度消失"）。

二、ReLU、Leaky ReLU 和 PReLU 的解决方案

1. ReLU：直接截断负区间

公式：

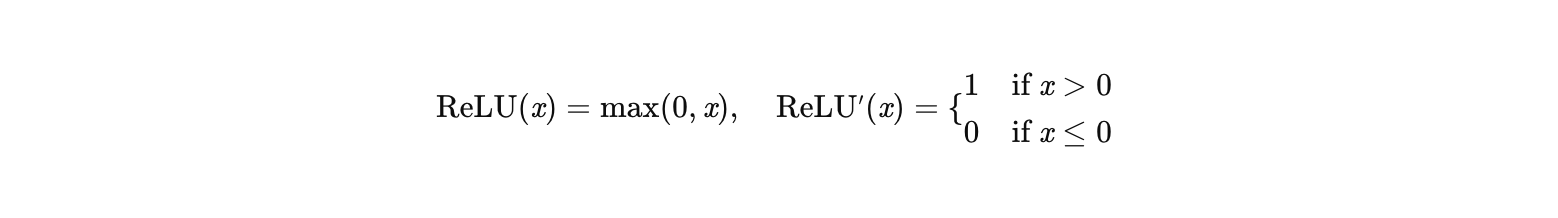
如何解决梯度消失？：

  • 正区间：梯度恒为 1，避免了 Sigmoid/Tanh 的梯度衰减。
  • 负区间 ：梯度为 0，虽然会导致神经元"死亡"，但在正区间梯度不会衰减，因此深层网络的梯度仍能传递。

例子 ：

假设一个 10 层网络，每层激活函数为 ReLU：

  • 若输入 x>0，则每层梯度为 1，最终梯度为 1^10=1（无衰减）。
  • 若某层输入 x≤0，则该层梯度为 0，后续层梯度也为 0（神经元死亡）。

问题 ：

ReLU 的负区间梯度为 0，可能导致部分神经元永远不激活（尤其在初始化不当或学习率过大时）。

2. Leaky ReLU：为负区间赋予微小梯度

公式：

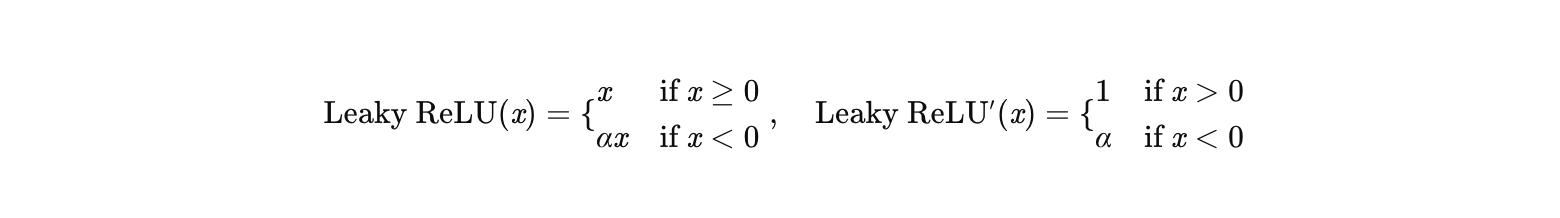
其中 α 是固定小常数（如 0.01）。

如何解决梯度消失？：

  • 正区间：梯度仍为 1，无衰减。
  • 负区间 ：梯度为 α（如 0.01），虽然小但不为 0，避免了神经元死亡，同时梯度衰减速度远慢于 Sigmoid/Tanh。

例子 ：

假设一个 10 层网络，每层激活函数为 Leaky ReLU（α=0.01）：

  • 若输入 x>0，梯度为 1^10=1。
  • 若输入 x<0，梯度为 0.01^10≈10−20（仍比 Sigmoid 的 0.25^10≈10−6 小得多，但不会完全消失）。

问题 ：

α 是固定值，可能对所有神经元不适用（例如某些特征需要更大的负区间梯度）。

3. PReLU：自适应学习负区间梯度

公式：

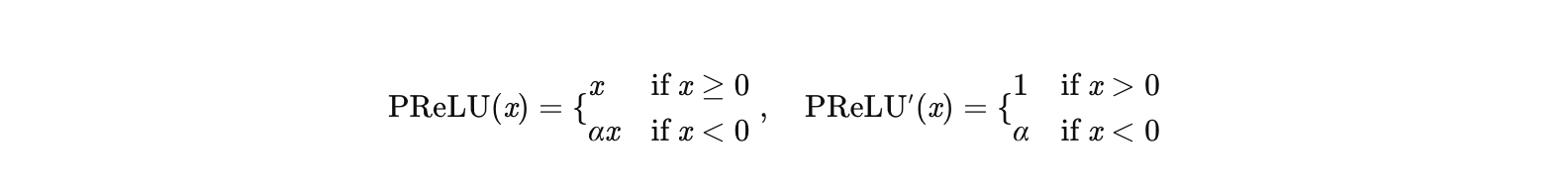
其中 α 是可学习的参数（通过反向传播更新）。

如何解决梯度消失？：

  • 正区间：梯度为 1，无衰减。
  • 负区间 ：梯度为 α（由数据驱动学习），自适应调整不同神经元的负区间梯度强度。

例子 ：

在推荐系统中，用户年龄和商品价格的分布差异大：

  • 年龄特征：负值可能表示"非目标年龄段"（如儿童），需较小梯度（α≈0.1）。
  • 价格特征：负值可能表示"低价商品"，需较大梯度（α≈0.3）。
    PReLU 可通过学习自动调整 α，而 Leaky ReLU 只能用固定 α（如 0.01），可能无法区分不同特征的重要性。

优势 ：

PReLU 的 α 初始值通常设为 0.25（经验值），并在训练中动态调整，避免手动调参的麻烦。

三、对比总结

激活函数 正区间梯度 负区间梯度 如何解决梯度消失 适用场景
Sigmoid σ(x)(1−σ(x))（最大 0.25） 同正区间 梯度逐层衰减 已淘汰
Tanh 1−tanh2(x)（最大 1） 同正区间 梯度仍可能衰减 已淘汰
ReLU 1 0 正区间无衰减，负区间神经元死亡 简单任务（如 MNIST）
Leaky ReLU 1 α（固定） 负区间梯度微小但不为 0 需避免神经元死亡的场景
PReLU 1 α（可学习） 负区间梯度自适应调整 复杂任务（如推荐系统、NLP）

四、关键结论

  1. ReLU 通过直接截断负区间，彻底避免了正区间的梯度衰减，但可能导致神经元死亡。
  2. Leaky ReLU 通过固定负区间梯度（如 0.01），缓解了神经元死亡问题，但无法自适应不同数据分布。
  3. PReLU 通过学习负区间梯度，进一步提升了模型的灵活性，尤其适合复杂任务（如推荐系统、NLP）。

实际应用建议：

  • 从 ReLU 开始尝试，若遇到神经元死亡问题，换用 Leaky ReLU 或 PReLU。
  • 在计算资源充足时，优先选择 PReLU（尤其是数据分布复杂时）。

二、进一步延伸PReLU

在推荐系统中，PReLU（Parametric ReLU）能够针对不同特征（如用户年龄、商品价格）自动调整负区间的梯度参数 α，其核心机制在于 α 是可学习的参数，且每个特征通道（或神经元）独立拥有自己的 α,（一般是共享，需要设置）。这种设计使得模型能够根据数据的分布特性，自适应地优化负区间的梯度行为。以下从原理、实现和例子三方面详细解释

一、PReLU 的核心机制：通道级可学习 α

1. α 的学习方式

  • 传统 Leaky ReLU：α 是全局固定值（如 0.01），对所有特征和神经元一视同仁。
  • PReLU ：α 是可学习的参数 ，通过反向传播独立更新。具体实现中，α 通常按特征通道（Channel） 或神经元 维度定义：
    • 通道级 α：每个输入特征通道（如年龄、价格）拥有独立的 α。
    • 神经元级 α：每个神经元拥有独立的 α（更灵活，但参数量更大）。

数学表达 ：

对于输入特征向量 x=[x1​,x2​,...,xC​]（C 为特征维度），PReLU 的输出为：

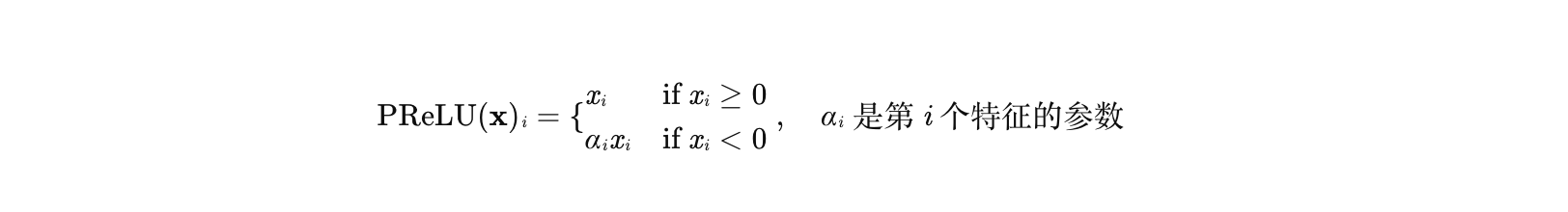
2. α 如何与特征关联？

  • 数据驱动学习：α 的初始值通常设为 0.25（经验值），但在训练过程中会根据特征的分布自动调整：

    • 若某特征（如年龄）的负值对任务影响较小（如"非目标年龄段"），α 会逐渐趋近于 0（抑制负区间梯度）。
    • 若某特征（如价格）的负值对任务重要（如"低价商品"），α 会逐渐增大（增强负区间梯度）。

  • 梯度更新：α 的梯度通过反向传播计算，公式为：

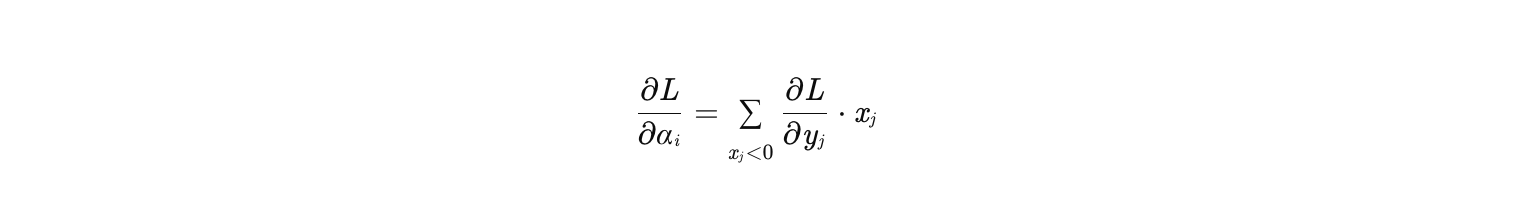
  • 其中 yj​=αi​*xj​ 是 PReLU 的输出。这表明 α 的更新依赖于负区间样本的梯度贡献。

二、为什么 PReLU 能区分不同特征的重要性？

1. 特征分布差异的直观解释

以推荐系统中的用户年龄和商品价格为例：

  • 年龄特征 ：
    • 负值可能表示"非目标年龄段"（如儿童或老年人），这些用户对推荐结果影响较小。
    • 此时，负区间的梯度应较小（α≈0.1），避免模型过度关注无关年龄段。
  • 价格特征 ：
    • 负值可能表示"低价商品"（如通过归一化或编码后的值），这些商品对推荐结果影响较大（如促销商品）。
    • 此时，负区间的梯度应较大（α≈0.3），确保模型能捕捉低价商品的信号。

2. PReLU 的自适应调整过程

假设初始时所有特征的 α=0.25，训练过程中：

  1. 年龄特征 ：
    • 若负区间样本的梯度贡献较小（如"非目标年龄段"的损失变化不大），α 会通过梯度下降逐渐减小（如从 0.25 降到 0.1）。
  2. 价格特征 ：
    • 若负区间样本的梯度贡献较大（如"低价商品"的损失显著下降），α 会逐渐增大（如从 0.25 升到 0.3）。

最终，不同特征的 α 会收敛到不同值，反映它们在任务中的重要性差异。

三、与 Leaky ReLU 的对比：固定 α 的局限性

Leaky ReLU 的 α 是全局固定值（如 0.01），无法区分不同特征的重要性：

  • 年龄特征：若用 α=0.01，负区间梯度过小，可能完全忽略"非目标年龄段"的微弱信号。
  • 价格特征：若用 α=0.01，负区间梯度仍过小，可能无法充分捕捉"低价商品"的关键信息。

而 PReLU 通过为每个特征学习独立的 α，能够：

  1. 保留重要特征的负区间信息（如价格特征的 α=0.3）。
  2. 抑制无关特征的负区间噪声（如年龄特征的 α=0.1）。

四、实际代码示例（PyTorch 实现）

以下代码主要展示PReLU，和alpha的变化：

python 复制代码 
class PReLU(nn.Module):
    def __init__(self,num_parameters,alpha_init= 0.25):
        super(PReLU,self).__init__()
        self.weight = nn.Parameter(torch.full((num_parameters,), alpha_init),requires_grad=True)

    def forward(self,X):
        # p = torch.where(X > 0,torch.tensor(1.0),torch.tensor(0.0))
        p = (X > 0).float()  # 更高效的掩码计算
        output = p*X + (1-p)* self.weight * X      
        return output

import torch
import torch.nn as nn

# 定义通道级 PReLU（num_parameters=特征维度）
prelu = PReLU(num_parameters=2)  # 假设输入有2个特征（年龄、价格）
# 初始化参数（默认初始值为0.25）
print("初始 alpha:", prelu.weight)  # 输出: tensor([0.2500, 0.2500], requires_grad=True)
# 模拟训练过程：输入包含年龄和价格的负值样本
x = torch.tensor([[-1.0, -1.0], [-1.0, -3.0]], requires_grad=True)  # 2个样本，2个特征
output = prelu(x)
print("输出结果：",output)
loss = output.sum()

# 反向传播更新 alpha
loss.backward()

optimizer = torch.optim.SGD([prelu.weight], lr=0.01)
optimizer.step()

# 观察 alpha 的更新
print("更新后 grad:",  prelu.weight.grad)
print("更新后 alpha:", prelu.weight)  # 输出: tensor([0.2700, 0.2900], requires_grad=True)
复制代码 
初始 alpha: Parameter containing:
tensor([0.2500, 0.2500], requires_grad=True)
输出结果： tensor([[-0.2500, -0.2500],
        [-0.2500, -0.7500]], grad_fn=<AddBackward0>)
更新后 grad: tensor([-2., -4.])
更新后 alpha: Parameter containing:
tensor([0.2700, 0.2900], requires_grad=True)

这里解释下：

输入： [-1,-1] [-1,-3]

输出结果：-0.25 = p*x +(1-p)*alpha*x = alpha*x = 0.25*(-1),其余同理

梯度：-2 = (1-p)*x = x = [-1 + -1] = [-2],另一个元素同理

更新后的alpha： 0.27 = 0.25 - （-2*0.01）= 0.27

经过一次反向传播后，α 根据负区间样本的梯度贡献自动调整（如年龄特征的 α 减小，价格特征的 α 增大）-和示例无关哈～

总结：alpha如果变大，证明特征信息重要，反之，不重要被抑制。

五、总结

  1. PReLU 的 α 是可学习的参数，且通常按特征通道或神经元维度定义。
  2. α 与特征关联：通过反向传播根据特征的负区间梯度贡献自动调整，反映特征在任务中的重要性。
  3. 优势：相比 Leaky ReLU 的固定 α，PReLU 能更灵活地处理不同特征的分布差异，提升模型性能。
  4. 应用场景：推荐系统、NLP 等需要区分特征重要性的任务中，PReLU 是比 Leaky ReLU 更好的选择。

三、Dice

在深度学习模型中，PReLU（Parametric ReLU） 和**Dice（Data-driven Adaptive Activation）**是两种改进的激活函数，用于解决传统ReLU的缺陷（如"死亡神经元"问题）。DIN（Deep Interest Network）将PReLU替换为Dice，是为了更灵活地适应推荐系统中数据分布的动态变化。以下结合原理和具体例子详细讲解：

一、PReLU的作用与局限性

1. PReLU的原理

PReLU是ReLU的改进版本，通过引入可学习的参数α控制负区间的斜率：

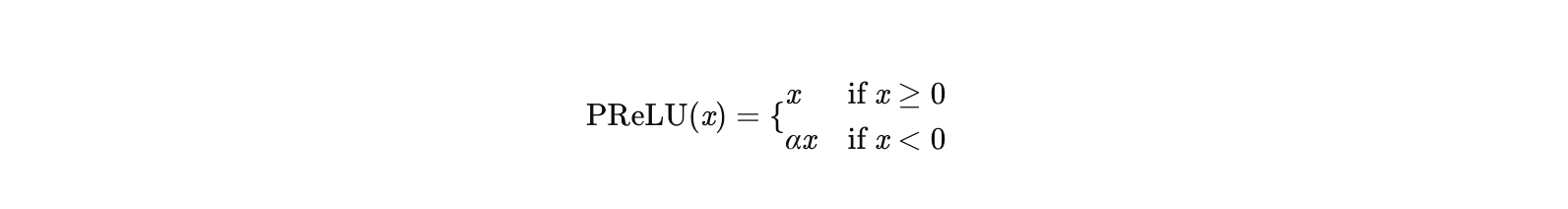
其中：

  • α 是可学习的参数（通常初始化为0.25），通过反向传播更新。
  • 优势：相比ReLU（负区间恒为0），PReLU允许负值有一定梯度，缓解"死亡神经元"问题。
2. PReLU的局限性
  • 固定校正点：PReLU的校正点（0）是固定的，但推荐系统中不同特征（如用户年龄、商品价格）的分布差异大，固定点可能无法适应所有场景。
  • 全局参数共享：所有神经元共享同一个α，无法针对不同数据分布动态调整。

二、Dice的改进：数据驱动的自适应激活

Dice是DIN提出的一种自适应激活函数，其核心思想是根据输入数据的分布动态调整校正点（Pivot）和负区间的斜率。公式如下：

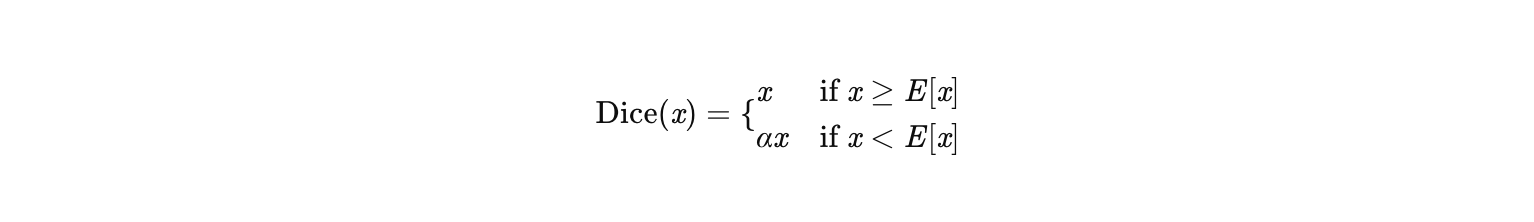
其中：

  • E[x] 是输入数据x的均值（动态计算，通常用批归一化后的均值）。

  • α 是可学习的参数（控制负区间的斜率）。

  • 平滑过渡：为避免校正点附近梯度突变，Dice引入平滑函数：

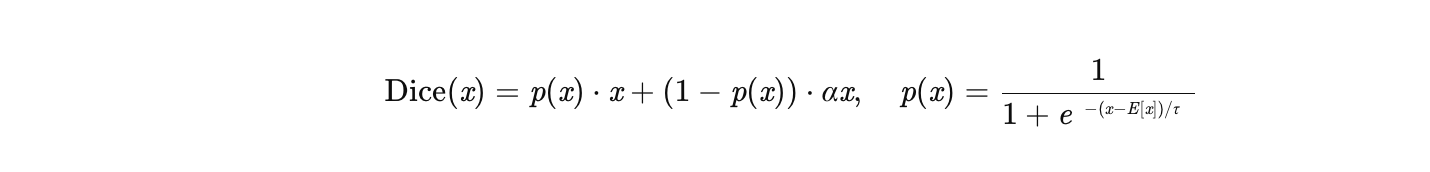
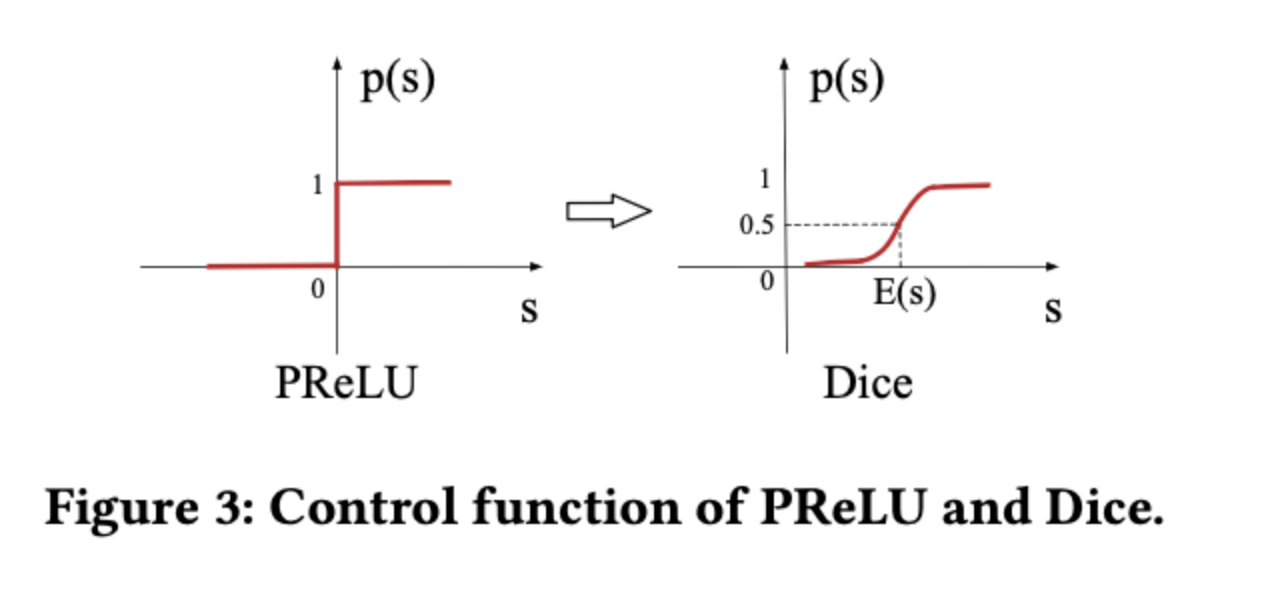
其中 τ 是温度系数（控制平滑程度）。越大越平滑，反之越不平滑

Dice的优势
  1. 动态校正点：校正点由数据均值E[x]决定，适应不同特征的分布（如年龄和价格的均值不同）。
  2. 自适应斜率：α可学习，负区间的梯度根据数据动态调整。
  3. 平滑过渡：避免PReLU在校正点处的梯度突变问题。

三、DIN中替换PReLU为Dice的动机

DIN的核心是通过注意力机制动态捕捉用户兴趣，但用户行为数据具有以下特点：

  1. 稀疏性：每个用户的交互商品数量差异大（如活跃用户vs.新用户）。
  2. 多样性：用户兴趣跨多个领域（如同时喜欢电子产品和服装）。
  3. 动态性：用户兴趣随时间快速变化（如季节性商品）。

PReLU的不足 ：

固定校正点（0）无法适应不同用户行为数据的分布差异。例如：

  • 对历史行为少的用户，输入特征均值可能偏低，PReLU的负区间梯度可能误导模型。
  • 对高频用户，输入特征均值高，PReLU的正区间可能过度激活。

Dice的适配性 ：

Dice通过动态计算E[x]，自动适应不同用户的数据分布。例如：

  • 对历史行为少的用户，E[x]较低，Dice会减少负区间的梯度，避免过拟合噪声。
  • 对高频用户，E[x]较高，Dice会增强正区间的梯度，突出主要兴趣。

五、总结

特性 PReLU Dice
校正点 固定为0 动态为输入数据的均值E[x]
负区间斜率 固定α 可学习α，且通过平滑函数过渡
适用场景 通用深度学习任务 推荐系统等数据分布动态变化的场景
DIN中的优势 无法适应稀疏/密集用户差异 自动平衡不同用户的数据分布，提升泛化能力

DIN替换PReLU为Dice的核心原因 ：

推荐系统中用户行为数据分布差异大，Dice通过动态校正点和自适应斜率，能更精细地捕捉用户兴趣的多样性，从而提升模型性能（如点击率预测准确率）。

再次回到这个图，简要总结几句，其实，比较直观

prelu是固定的校正点（0），而dice是均值，针对不同用户的不同特征，可以更好更准确的识别正信号和负信号,同时在均值附近加了平滑。随着用户的购物记录频次增加，对于用户的刻画会更加精准，比如价格，如果用户消费100次，均值在200左右，那么当遇到一个候选商品是100和300的时候，差值是不一样的.

python 复制代码 
#dice
import numpy as np
def px_dice(x):
    p  =1 / (1+(np.exp(-(x-200)/1)))
    return p
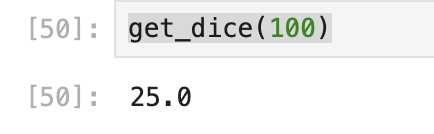
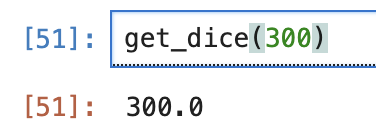
def get_dice(x):
    output = px_dice(x)*x + (1-px_dice(x))*0.25*x
    return output
#prelu
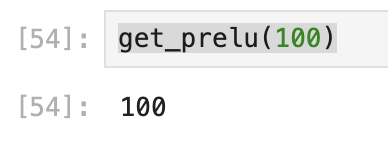
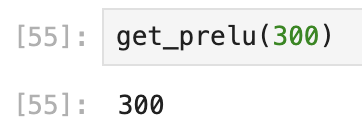
def get_prelu(x):
    if x >= 0:
        return x
    elif x < 0:
        return 0.25*x

dice(alpha 默认0.25)

  • 100元候选： 100<200:
  • 300元候选：300>200:

relu(alpha 默认0.25)

  • 100元候选： 100<200:
  • 300元候选：300>200:

可以粗略的看出来，dice的gap会更大。

到这里基本描述清楚了这套激活函数的产生，以及详细的变化和使用，大家如果还有什么问题，欢迎及时评论交流哈～。

相关推荐
flying_13146 天前
推荐系统分享系列-DIN(Deep Interest Network for Click-Through Rate Prediction)（一）
推荐系统·激活函数·din·注意力单元·prelu·dice·小批量感知正则化
Java后端的Ai之路19 天前
【神经网络基础】-一个完整的神经网络学习过程是怎样的？
人工智能·深度学习·神经网络·学习·激活函数
Java后端的Ai之路20 天前
【神经网络基础】-激活函数详解
人工智能·深度学习·神经网络·激活函数
oscar99921 天前
激活函数：神经网络的“开关”与“灵魂”
人工智能·深度学习·神经网络·激活函数
最晚的py21 天前
激活函数对比大全
深度学习·激活函数
core51222 天前
ReLU 激活函数：神经网络的“开关”
人工智能·深度学习·神经网络·relu
Yongqiang Cheng1 个月前
ReLU Function and Leaky ReLU Function - Derivatives and Gradients (导数和梯度)
梯度·导数·relu·gradients·derivatives·leaky relu
大千AI助手2 个月前
Sigmoid函数：从生物生长曲线到神经网络激活的桥梁
人工智能·神经网络·机器学习·激活函数·sigmoid·大千ai助手·lr
大千AI助手2 个月前
Softmax函数：深度学习中的多类分类基石与进化之路
人工智能·深度学习·机器学习·分类·softmax·激活函数·大千ai助手
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）03Linux下V2Ray安装配置指南042025年大语言模型技术全景报告05UV安装并设置国内源06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07BongoCat - 跨平台键盘猫动画工具08Labelme从安装到标注：零基础完整指南09jdk21下载、安装（Windows、Linux、macOS）10Claude Code Skills 实用使用手册