ReLU Function and Leaky ReLU Function - Derivatives and Gradients (导数和梯度)

Yongqiang Cheng2025-12-21 15:34

ReLU Function and Leaky ReLU Function - Derivatives and Gradients {导数和梯度}

  • [1. ReLU (Rectified Linear Unit) Function](#1. ReLU (Rectified Linear Unit) Function)
    • [1.1. Parameters](#1.1. Parameters)
    • [1.2. Shape](#1.2. Shape)
  • [2. LeakyReLU (Leaky Rectified Linear Unit)](#2. LeakyReLU (Leaky Rectified Linear Unit))
    • [2.1. Parameters](#2.1. Parameters)
    • [2.2. Shape](#2.2. Shape)
  • [3. ReLU Function - Derivatives and Gradients (导数和梯度)](#3. ReLU Function - Derivatives and Gradients (导数和梯度))
    • [3.1. PyTorch `torch.nn.ReLU(inplace=False)`](#3.1. PyTorch torch.nn.ReLU(inplace=False))
    • [3.2. Python ReLU Function](#3.2. Python ReLU Function)
    • [3.3. Python ReLU Function](#3.3. Python ReLU Function)
  • [4. Leaky ReLU Function - Derivatives and Gradients (导数和梯度)](#4. Leaky ReLU Function - Derivatives and Gradients (导数和梯度))
    • [4.1. PyTorch `torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)`](#4.1. PyTorch torch.nn.LeakyReLU(negative_slope=0.01, inplace=False))
    • [4.2. Python Leaky ReLU Function](#4.2. Python Leaky ReLU Function)
    • [4.3. Python Leaky ReLU Function](#4.3. Python Leaky ReLU Function)
  • References

Activation functions decide whether a neuron should be activated or not by calculating the weighted sum and further adding bias to it. They are differentiable operators for transforming input signals to outputs, while most of them add nonlinearity.

激活函数 (activation function) 通过计算加权和并加上偏置来确定神经元是否应该被激活，它们将输入信号转换为输出的可微运算。大多数激活函数都是非线性的。

1. ReLU (Rectified Linear Unit) Function

class torch.nn.ReLU(inplace=False)
https://docs.pytorch.org/docs/stable/generated/torch.nn.ReLU.html

torch.nn.functional.relu(input, inplace=False) -> Tensor
https://docs.pytorch.org/docs/stable/generated/torch.nn.functional.relu.html

https://github.com/pytorch/pytorch/blob/main/torch/nn/modules/activation.py

ReLU provides a very simple nonlinear transformation.

ReLU 提供了一种非常简单的非线性变换。

Applies the rectified linear unit function element-wise.

The definition of the ReLU function:

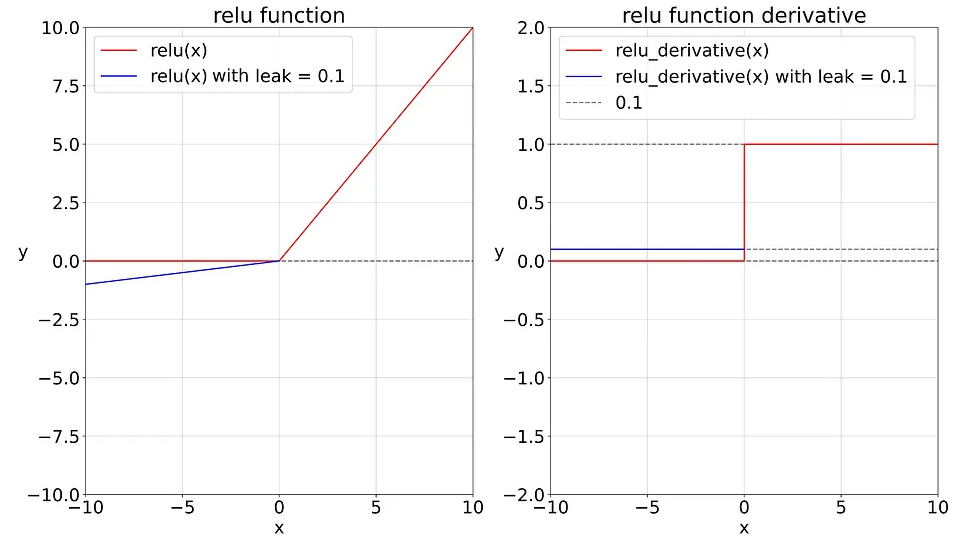
ReLU ( x ) = max ⁡ ( 0 , x ) = x + ∣ x ∣ 2 = { x , x > 0 0 , x ≤ 0 \begin{aligned} \text{ReLU}(x) &= \max(0, x) = \frac{x+|x|}{2} \\ &= \begin{cases} x, & x > 0 \\ 0, & x \le 0 \\ \end{cases} \end{aligned} ReLU(x)=max(0,x)=2x+∣x∣={x,0,x>0x≤0

The ReLU function retains only positive elements and discards all negative elements by setting the corresponding activations to 0.

ReLU 函数通过将相应的活性值设为 0，仅保留正元素并丢弃所有负元素。

The derivative of the ReLU function:

d y d x = f ′ ( x ) = d ( { x , x > 0 0 , x ≤ 0 ) d x = { 1 , x > 0 0 , x ≤ 0 \begin{aligned} \frac{dy}{dx} &= f'(x) \\ &= \frac{d \left( {\begin{cases} x, & x > 0 \\ 0, & x \le 0 \\ \end{cases}} \right) }{dx} \\ &= \begin{cases} 1, & x > 0 \\ 0, & x \le 0 \\ \end{cases} \\ \end{aligned} dxdy=f′(x)=dxd({x,0,x>0x≤0)={1,0,x>0x≤0

When the input is negative, the derivative of the ReLU function is 0, and when the input is positive, the derivative of the ReLU function is 1. Note that the ReLU function is not differentiable when the input takes value precisely equal to 0. In these cases, we default to the left-hand-side derivative and say that the derivative is 0 when the input is 0. We can get away with this because the input may never actually be zero (mathematicians would say that it is nondifferentiable on a set of measure zero).

当输入为负时，ReLU 函数的导数为 0，而当输入为正时，ReLU 函数的导数为 1。注意，当输入值精确等于 0 时，ReLU 函数不可导。在此时，我们默认使用左侧的导数，即当输入为 0 时导数为 0。我们可以忽略这种情况，因为输入可能永远都不会是 0。

The reason for using ReLU is that its derivatives are particularly well behaved: either they vanish or they just let the argument through. This makes optimization better behaved and it mitigated the well-documented problem of vanishing gradients that plagued previous versions of neural networks.

使用 ReLU 的原因是，它求导表现得特别好：要么让参数消失，要么让参数通过。这使得优化表现得更好，并且 ReLU 减轻了困扰以往神经网络的梯度消失问题。

复制代码 
plague [pleɪɡ]
n. 瘟疫；死亡率高的传染病；祸患
v. 困扰；折磨；给...造成长时间的痛苦或麻烦；使受煎熬

1.1. Parameters

  • inplace (bool) - can optionally do the operation in-place. Default: False

1.2. Shape

  • Input : (*), where * means any number of dimensions.

  • Output : (*), same shape as the input.

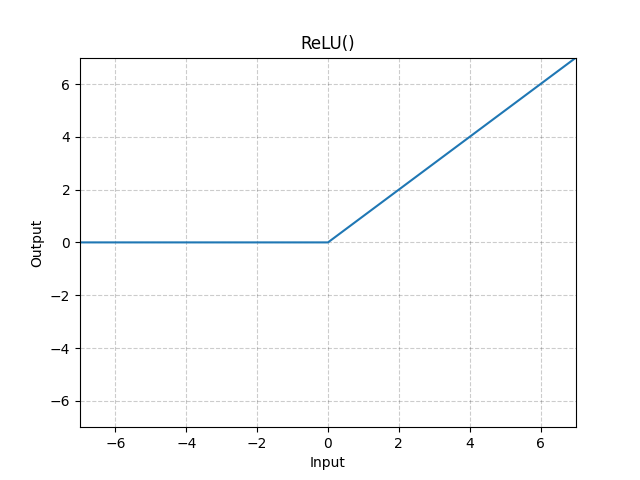
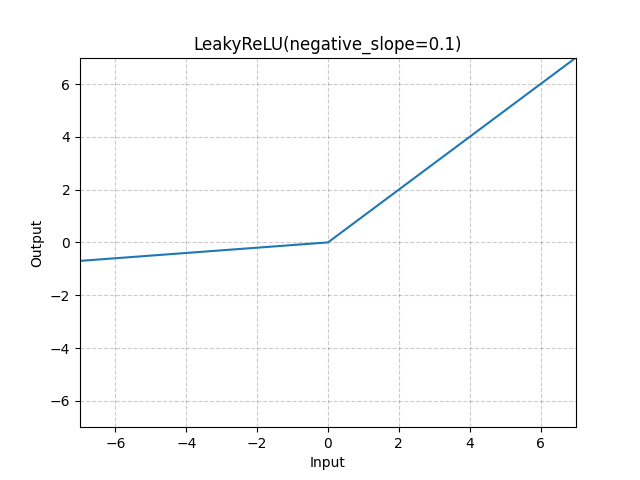
2. LeakyReLU (Leaky Rectified Linear Unit)

class torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)
https://docs.pytorch.org/docs/stable/generated/torch.nn.LeakyReLU.html

torch.nn.functional.leaky_relu(input, negative_slope=0.01, inplace=False) -> Tensor
https://docs.pytorch.org/docs/stable/generated/torch.nn.functional.leaky_relu.html

https://github.com/pytorch/pytorch/blob/main/torch/nn/modules/activation.py

Applies the LeakyReLU function element-wise.

The definition of the Leaky ReLU function:

LeakyReLU ( x ) = max ⁡ ( 0 , x ) + negative_slope ∗ min ⁡ ( 0 , x ) = { x , x ≥ 0 negative_slope ∗ x , otherwise \begin{aligned} \text{LeakyReLU}(x) &= \max(0, x) + \text{negative\_slope} * \min(0, x) \\ &= \begin{cases} x, & x \geq 0 \\ \text{negative\_slope} * x, & \text{ otherwise } \end{cases} \end{aligned} LeakyReLU(x)=max(0,x)+negative_slope∗min(0,x)={x,negative_slope∗x,x≥0 otherwise

The derivative of the Leaky ReLU function:

d y d x = f ′ ( x ) = d ( { x , x ≥ 0 negative_slope ∗ x , otherwise ) d x = { 1 , x ≥ 0 negative_slope , x < 0 \begin{aligned} \frac{dy}{dx} &= f'(x) \\ &= \frac{d \left( \begin{cases} x, & x \geq 0 \\ \text{negative\_slope} * x, & \text{ otherwise } \end{cases} \right) }{dx} \\ &= \begin{cases} 1, & x \geq 0 \\ \text{negative\_slope}, & x < 0 \\ \end{cases} \\ \end{aligned} dxdy=f′(x)=dxd({x,negative_slope∗x,x≥0 otherwise )={1,negative_slope,x≥0x<0

在 x = 0 x = 0 x=0 处，Leaky ReLU 函数的导数函数是不连续的。

2.1. Parameters

  • negative_slope (float) - Controls the angle of the negative slope (which is used for negative input values). Default: 1e-2

  • inplace (bool) - can optionally do the operation in-place. Default: False

2.2. Shape

  • Input : (*) where * means, any number of additional dimensions

  • Output : (*), same shape as the input

This is the graph for the ReLU and Leaky ReLU functions and their derivatives.

3. ReLU Function - Derivatives and Gradients (导数和梯度)

3.1. PyTorch torch.nn.ReLU(inplace=False)

复制代码 
# !/usr/bin/env python
# coding=utf-8

import torch
import torch.nn as nn

torch.set_printoptions(precision=6)

input = torch.tensor([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=torch.float, requires_grad=True)

print(f"input.requires_grad: {input.requires_grad}, input.shape: {input.shape}")

relu = nn.ReLU()
forward_output = relu(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/relu.py 
input.requires_grad: True, input.shape: torch.Size([2, 3])

forward_output.shape: torch.Size([2, 3])
Forward Pass Output:
tensor([[0.000000, 0.000000, 1.500000],
        [0.500000, 0.000000, 3.000000]], grad_fn=<ReluBackward0>)

Process finished with exit code 0

3.2. Python ReLU Function

复制代码 
# !/usr/bin/env python
# coding=utf-8

import numpy as np

np.set_printoptions(threshold=np.inf)


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class ReLULayer:
    """
    Rectified Linear Unit (ReLU) activation function layer
    """

    def __init__(self):
        # Cache the input for the backward pass (gradient calculation)
        self.input = None

    def forward(self, input):
        """
        Performs the forward pass for the relu function: output = max(0, input)
        f(x) = max(0, x)
        """

        self.input = input
        # Returns the input directly if positive, otherwise 0
        self.output = np.maximum(0, input)
        return self.output

    def backward(self, upstream_gradient):
        """
        Calculates the gradient of the ReLU function with respect to the input x
        The derivative of the relu function is 1 for x > 0 and 0 for x <= 0
        """

        # Create an array of the same shape as the input 'x', initialized to zeros
        relu_derivative = np.zeros_like(self.input)
        relu_derivative[self.input > 0] = 1
        print(f"\nrelu_derivative.shape: {relu_derivative.shape}")
        print(f"ReLU Derivative:\n{relu_derivative}")

        # Apply the chain rule: multiply the derivative by the upstream gradient
        downstream_gradient = upstream_gradient * relu_derivative
        return downstream_gradient


relu_layer = ReLULayer()

input = np.array([-1.5, 0.0, 1.5, 0.5, -2.0, 3.0], dtype=np.float32)

# Forward pass
forward_output = relu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = relu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/relu.py 

forward_output.shape: (6,)
Forward Pass Output:
[0.  0.  1.5 0.5 0.  3. ]

relu_derivative.shape: (6,)
ReLU Derivative:
[0. 0. 1. 1. 0. 1.]

backward_output.shape: (6,)
Backward Pass Output:
[0.  0.  0.1 0.1 0.  0.1]

Process finished with exit code 0

3.3. Python ReLU Function

复制代码 
# !/usr/bin/env python
# coding=utf-8

import numpy as np

np.set_printoptions(threshold=np.inf)


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class ReLULayer:
    """
    Rectified Linear Unit (ReLU) activation function layer
    """

    def __init__(self):
        # Cache the input for the backward pass (gradient calculation)
        self.input = None

    def forward(self, input):
        """
        Performs the forward pass for the relu function: output = max(0, input)
        f(x) = max(0, x)
        """

        self.input = input
        # Returns the input directly if positive, otherwise 0
        self.output = np.maximum(0, input)
        return self.output

    def backward(self, upstream_gradient):
        """
        Calculates the gradient of the ReLU function with respect to the input x
        The derivative of the relu function is 1 for x > 0 and 0 for x <= 0
        """

        # Create an array of the same shape as the input 'x', initialized to zeros
        relu_derivative = np.zeros_like(self.input)
        relu_derivative[self.input > 0] = 1
        print(f"\nrelu_derivative.shape: {relu_derivative.shape}")
        print(f"ReLU Derivative:\n{relu_derivative}")

        # Apply the chain rule: multiply the derivative by the upstream gradient
        downstream_gradient = upstream_gradient * relu_derivative
        return downstream_gradient


relu_layer = ReLULayer()

input = np.array([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=np.float32)

# Forward pass
forward_output = relu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = relu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/relu.py 

forward_output.shape: (2, 3)
Forward Pass Output:
[[0.  0.  1.5]
 [0.5 0.  3. ]]

relu_derivative.shape: (2, 3)
ReLU Derivative:
[[0. 0. 1.]
 [1. 0. 1.]]

backward_output.shape: (2, 3)
Backward Pass Output:
[[0.  0.  0.1]
 [0.1 0.  0.1]]

Process finished with exit code 0

4. Leaky ReLU Function - Derivatives and Gradients (导数和梯度)

4.1. PyTorch torch.nn.LeakyReLU(negative_slope=0.01, inplace=False)

复制代码 
# !/usr/bin/env python
# coding=utf-8

import torch
import torch.nn as nn

torch.set_printoptions(precision=6)

input = torch.tensor([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=torch.float, requires_grad=True)

print(f"input.requires_grad: {input.requires_grad}, input.shape: {input.shape}")

leaky_relu = nn.LeakyReLU(negative_slope=0.1)
forward_output = leaky_relu(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/leaky_relu.py 
input.requires_grad: True, input.shape: torch.Size([2, 3])

forward_output.shape: torch.Size([2, 3])
Forward Pass Output:
tensor([[-0.150000,  0.000000,  1.500000],
        [ 0.500000, -0.200000,  3.000000]], grad_fn=<LeakyReluBackward0>)

Process finished with exit code 0

4.2. Python Leaky ReLU Function

复制代码 
# !/usr/bin/env python
# coding=utf-8

import numpy as np

np.set_printoptions(threshold=np.inf)


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class LeakyReLULayer:
    """
    Leaky Rectified Linear Unit (Leaky ReLU) activation function
    """

    def __init__(self, negative_slope=0.2):
        # Cache the input for the backward pass (gradient calculation)
        self.input = None
        self.negative_slope = negative_slope

    def forward(self, input):
        """
        Applies the Leaky ReLU function: f(x) = x if x > 0, else negative_slope * x
        """

        self.input = input
        # Apply the Leaky ReLU function: x for positive values, negative_slope * x for negative values
        self.output = np.where(input >= 0, input, self.negative_slope * input)
        return self.output

    def backward(self, upstream_gradient):
        """
        Calculates the gradient of the Leaky ReLU function with respect to the input x
        The derivative of the Leaky ReLU function is 1 if x > 0, else negative_slope
        """

        # Create an array of the same shape as the input 'x', initialized to zeros
        leaky_relu_derivative = np.ones_like(self.input)
        leaky_relu_derivative[self.input < 0] = self.negative_slope
        print(f"\nleaky_relu_derivative.shape: {leaky_relu_derivative.shape}")
        print(f"Leaky ReLU Derivative:\n{leaky_relu_derivative}")

        # Apply the chain rule: multiply the derivative by the upstream gradient
        downstream_gradient = upstream_gradient * leaky_relu_derivative
        return downstream_gradient


leaky_relu_layer = LeakyReLULayer()

input = np.array([-1.5, 0.0, 1.5, 0.5, -2.0, 3.0], dtype=np.float32)

# Forward pass
forward_output = leaky_relu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = leaky_relu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/leaky_relu.py 

forward_output.shape: (6,)
Forward Pass Output:
[-0.3  0.   1.5  0.5 -0.4  3. ]

leaky_relu_derivative.shape: (6,)
Leaky ReLU Derivative:
[0.2 1.  1.  1.  0.2 1. ]

backward_output.shape: (6,)
Backward Pass Output:
[0.02 0.1  0.1  0.1  0.02 0.1 ]

Process finished with exit code 0

4.3. Python Leaky ReLU Function

复制代码 
# !/usr/bin/env python
# coding=utf-8

import numpy as np

np.set_printoptions(threshold=np.inf)


# numpy.multiply:
# Multiply arguments element-wise
# Equivalent to x1 * x2 in terms of array broadcasting

class LeakyReLULayer:
    """
    Leaky Rectified Linear Unit (Leaky ReLU) activation function
    """

    def __init__(self, negative_slope=0.2):
        # Cache the input for the backward pass (gradient calculation)
        self.input = None
        self.negative_slope = negative_slope

    def forward(self, input):
        """
        Applies the Leaky ReLU function: f(x) = x if x > 0, else negative_slope * x
        """

        self.input = input
        # Apply the Leaky ReLU function: x for positive values, negative_slope * x for negative values
        self.output = np.where(input >= 0, input, self.negative_slope * input)
        return self.output

    def backward(self, upstream_gradient):
        """
        Calculates the gradient of the Leaky ReLU function with respect to the input x
        The derivative of the Leaky ReLU function is 1 if x > 0, else negative_slope
        """

        # Create an array of the same shape as the input 'x', initialized to zeros
        leaky_relu_derivative = np.ones_like(self.input)
        leaky_relu_derivative[self.input < 0] = self.negative_slope
        print(f"\nleaky_relu_derivative.shape: {leaky_relu_derivative.shape}")
        print(f"Leaky ReLU Derivative:\n{leaky_relu_derivative}")

        # Apply the chain rule: multiply the derivative by the upstream gradient
        downstream_gradient = upstream_gradient * leaky_relu_derivative
        return downstream_gradient


leaky_relu_layer = LeakyReLULayer()

input = np.array([[-1.5, 0.0, 1.5], [0.5, -2.0, 3.0]], dtype=np.float32)

# Forward pass
forward_output = leaky_relu_layer.forward(input)
print(f"\nforward_output.shape: {forward_output.shape}")
print(f"Forward Pass Output:\n{forward_output}")

# Backward pass
upstream_gradient = np.ones(forward_output.shape) * 0.1
backward_output = leaky_relu_layer.backward(upstream_gradient)
print(f"\nbackward_output.shape: {backward_output.shape}")
print(f"Backward Pass Output:\n{backward_output}")

/home/yongqiang/miniconda3/bin/python /home/yongqiang/quantitative_analysis/leaky_relu.py 

forward_output.shape: (2, 3)
Forward Pass Output:
[[-0.3  0.   1.5]
 [ 0.5 -0.4  3. ]]

leaky_relu_derivative.shape: (2, 3)
Leaky ReLU Derivative:
[[0.2 1.  1. ]
 [1.  0.2 1. ]]

backward_output.shape: (2, 3)
Backward Pass Output:
[[0.02 0.1  0.1 ]
 [0.1  0.02 0.1 ]]

Process finished with exit code 0

References

1\] Yongqiang Cheng (程永强), \[2\] 动手学深度学习, \[3\] Deep Learning Tutorials, \[4\] Gradient boosting performs gradient descent, \[5\] Matrix calculus,

相关推荐
小毅&Nora10 小时前
【数学】【微积分】 ③ 导数的核心应用：从变化率到现实世界优化
微积分·导数
Yongqiang Cheng8 天前
Mean Absolute Error (MAE) Loss Function - Derivatives and Gradients (导数和梯度)
梯度·导数·mae·gradients·loss function·derivatives
噜～噜～噜～14 天前
偏导数和全导数的个人理解
深度学习·偏导数·梯度·全导数
西西弗Sisyphus19 天前
微积分中 为什么 dy/dx 有时候拆开，有时候是一个整体？
微积分·极限·导数·微分
xian_wwq2 个月前
【学习笔记】深度学习中梯度消失和爆炸问题及其解决方案研究
人工智能·深度学习·梯度
CLubiy2 个月前
【研究生随笔】Pytorch中的线性代数（微分）
人工智能·pytorch·深度学习·线性代数·梯度·微分
nju_spy3 个月前
南京大学 LLM开发基础（一）前向反向传播搭建
人工智能·pytorch·深度学习·大语言模型·梯度·梯度下降·反向传播
大千AI助手4 个月前
梯度消失问题：深度学习中的「记忆衰退」困境与解决方案
人工智能·深度学习·神经网络·梯度·梯度消失·链式法则·vanishing
大千AI助手4 个月前
梯度爆炸问题：深度学习中的「链式核弹」与拆弹指南
人工智能·深度学习·梯度·反向传播·梯度爆炸·指数效应·链式法则
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04BongoCat - 跨平台键盘猫动画工具05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06jdk21下载、安装（Windows、Linux、macOS）07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08Open-AutoGLM Windows 安装部署教程09sqli-labs靶场通关笔记：第18-19关 HTTP头部注入10Labelme从安装到标注：零基础完整指南