leetcode 3453(二分法)

sin_hielo2026-01-18 21:06

3453: 分割正方形Ⅰ

*思路：浮点二分

squares[i] = [xi, yi, li] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。

所有正方形的面积之和为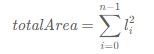

枚举正方形 (xi,++yi++ ,li)，如果水平线在正方形底边上方，即 yi<y，那么这个正方形在水平线下方的面积为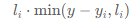

否则在水平线下方的面积为 0。

细节： 二分的左边界为 0，右边界为 max(yi+li)。++这里无需讨论开闭区间，因为我们算的是小数。++ 推荐的写法是固定一个循环次数，因为浮点数有舍入误差，可能算出的 mid 和 left 相等，此时 left=mid 不会更新 left，导致死循环。

循环次数：

复制代码

for(int i=0;i<47;i++){
    double mid=(left+right)/2;
    (check(mid)? right:left)=mid;
}
return (left+right)/2; //取中点误差极小

固定做 47 次二分（计算过程如上）

47 次可以把区间长度缩小到 (max_y-0)/2^47，对于 double 的 53 位有效精度来说已经足够

复制代码

class Solution {
public:
    double separateSquares(vector<vector<int>>& squares) {
        long long tot_area=0;
        int max_y=0;
        for(auto& sq:squares){
            int l=sq[2]; //正方形边长
            tot_area+=(long long)l*l;
            max_y=max(max_y,sq[1]+l);
        }
        auto check=[&](double y)->bool{
            double area=0;
            for(auto& sq:squares){
                double yi=sq[1];
                if(yi<y){
                    double l=sq[2];
                    area+=l*min(y-yi,l);
                }
            }
            return area>=tot_area/2.0; //返回true,说明可行y可以更小
        };
        double left=0,right=max_y;
        for(int i=0;i<47;i++){
            double mid=(left+right)/2;
            (check(mid)? right:left)=mid;
        }
        return (left+right)/2; //取中点误差极小
    }
};