强化学习入门到实战系列（四）马尔科夫决策过程

文章目录

- 一个简单的例子
- - 状态和动作
  - 策略定义

前面一节我们已经讨论到的马尔可夫过程和马尔可夫奖励过程都是自发改变的随机过程；而如果有一个外界的"刺激"来共同改变这个随机过程，就有了马尔可夫决策过程（Markov decision process，MDP）。我们将这个来自外界的刺激称为智能体（agent）的动作，在马尔可夫奖励过程（MRP）的基础上加入动作，就得到了马尔可夫决策过程（MDP）。MDP 与 MRP 非常相像，主要区别为 MDP 中的状态转移函数和奖励函数都比 MRP 多了作为自变量的动作 a 。

一个简单的例子

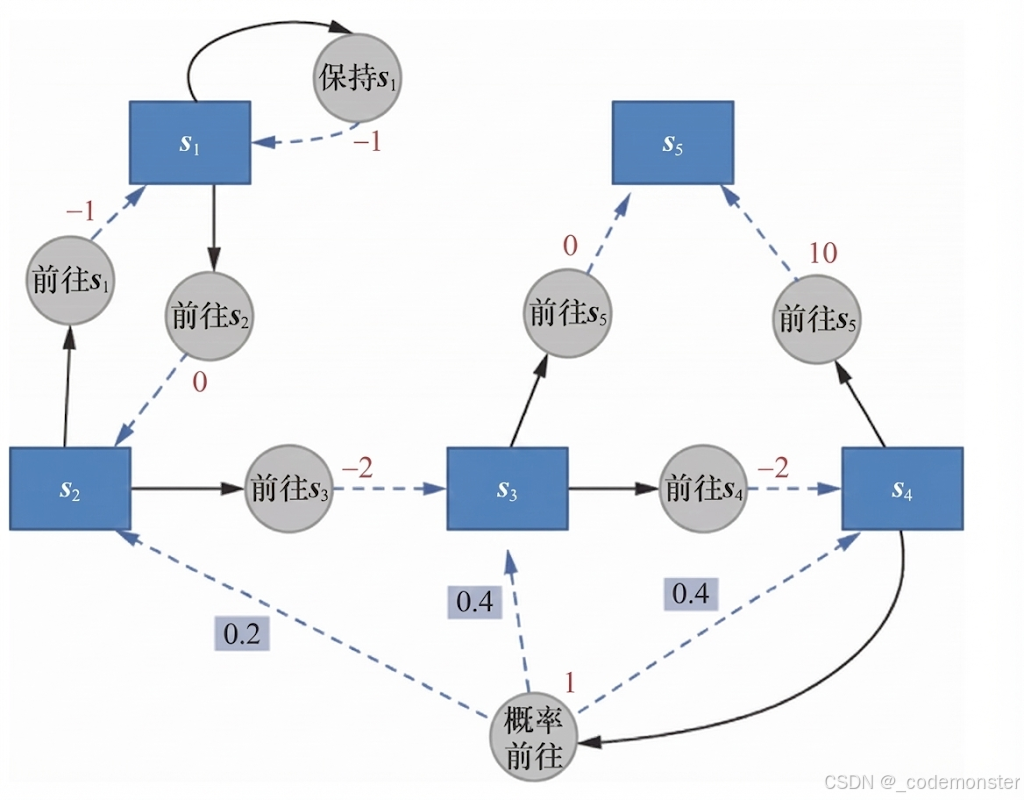
我们这里举一个简单的例子。下面的代码实现了上图的基本路线。

状态和动作

python 复制代码

S = ["s1", "s2", "s3", "s4", "s5"]  # 状态集合
A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"]  # 动作集合
# 状态转移函数
P = {
    "s1-保持s1-s1": 1.0,"s1-前往s2-s2": 1.0,
    "s2-前往s1-s1": 1.0,"s2-前往s3-s3": 1.0,
    "s3-前往s4-s4": 1.0,"s3-前往s5-s5": 1.0,
    "s4-前往s5-s5": 1.0,"s4-概率前往-s2": 0.2,
    "s4-概率前往-s3": 0.4,"s4-概率前往-s4": 0.4,
}
# 奖励函数
R = {
    "s1-保持s1": -1,"s1-前往s2": 0,
    "s2-前往s1": -1,"s2-前往s3": -2,
    "s3-前往s4": -2,"s3-前往s5": 0,
    "s4-前往s5": 10,"s4-概率前往": 1,
}
gamma = 0.5  # 折扣因子
MDP = (S, A, P, R, gamma)

MDP的基本元素

python 复制代码

S = ["s1", "s2", "s3", "s4", "s5"]  # 状态集合
A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"]  # 动作集合
gamma = 0.5  # 折扣因子

状态转移函数 P

python 复制代码

P = {
    "s1-保持s1-s1": 1.0,  # 在s1执行"保持s1"，100%留在s1
    "s1-前往s2-s2": 1.0,  # 在s1执行"前往s2"，100%到s2
    "s2-前往s1-s1": 1.0,  # 在s2执行"前往s1"，100%到s1
    "s2-前往s3-s3": 1.0,  # 在s2执行"前往s3"，100%到s3
    "s3-前往s4-s4": 1.0,  # 在s3执行"前往s4"，100%到s4
    "s3-前往s5-s5": 1.0,  # 在s3执行"前往s5"，100%到s5
    "s4-前往s5-s5": 1.0,  # 在s4执行"前往s5"，100%到s5
    "s4-概率前往-s2": 0.2,  # 在s4执行"概率前往"，20%到s2
    "s4-概率前往-s3": 0.4,  # 在s4执行"概率前往"，40%到s3
    "s4-概率前往-s4": 0.4,  # 在s4执行"概率前往"，40%留在s4
}

格式："当前状态-执行动作-下一状态"：转移概率
大部分是确定性转移（概率为1.0）
只有s4-概率前往是非确定性转移（概率分布）

奖励函数 R

python 复制代码

R = {
    "s1-保持s1": -1,     # 在s1保持，奖励-1
    "s1-前往s2": 0,      # 从s1去s2，奖励0
    "s2-前往s1": -1,     # 从s2去s1，奖励-1
    "s2-前往s3": -2,     # 从s2去s3，奖励-2
    "s3-前往s4": -2,     # 从s3去s4，奖励-2
    "s3-前往s5": 0,      # 从s3去s5，奖励0
    "s4-前往s5": 10,     # 从s4去s5，高奖励10
    "s4-概率前往": 1,     # 在s4概率前往，奖励1
}

格式："当前状态-执行动作"：即时奖励
s5是终止状态（没有从s5出发的转移）

策略定义

python 复制代码

# 策略1,随机策略
Pi_1 = {
    "s1-保持s1": 0.5,"s1-前往s2": 0.5,
    "s2-前往s1": 0.5,"s2-前往s3": 0.5,
    "s3-前往s4": 0.5, "s3-前往s5": 0.5,
    "s4-前往s5": 0.5,"s4-概率前往": 0.5,
}
# 策略2
Pi_2 = {
    "s1-保持s1": 0.6,"s1-前往s2": 0.4,
    "s2-前往s1": 0.3,"s2-前往s3": 0.7,
    "s3-前往s4": 0.5,"s3-前往s5": 0.5,
    "s4-前往s5": 0.1,"s4-概率前往": 0.9,
}


# 把输入的两个字符串通过"-"连接,便于使用上述定义的P、R变量
def join(str1, str2):
    return str1 + '-' + str2

策略1（Pi_1）随机策略：

python 复制代码

Pi_1 = {
    "s1-保持s1": 0.5, "s1-前往s2": 0.5,      # s1：50%保持，50%去s2
    "s2-前往s1": 0.5, "s2-前往s3": 0.5,      # s2：50%去s1，50%去s3
    "s3-前往s4": 0.5, "s3-前往s5": 0.5,      # s3：50%去s4，50%去s5
    "s4-前往s5": 0.5, "s4-概率前往": 0.5,     # s4：50%直接去s5，50%概率前往
}

策略2（Pi_2）非均匀策略：

python 复制代码

Pi_2 = {
    "s1-保持s1": 0.6, "s1-前往s2": 0.4,      # s1：更倾向于保持(60%)
    "s2-前往s1": 0.3, "s2-前往s3": 0.7,      # s2：更倾向于去s3(70%)
    "s3-前往s4": 0.5, "s3-前往s5": 0.5,      # s3：均匀分布
    "s4-前往s5": 0.1, "s4-概率前往": 0.9,     # s4：非常倾向于概率前往(90%)
}

辅助函数 join

python 复制代码

def join(str1, str2):
    return str1 + '-' + str2

用于将状态和动作拼接成"状态-动作"格式
便于访问R和Pi字典（这些字典使用这种格式作为键）