【实战】预测 4 天后的卫星位置 —— 考虑 J2 摄动 (例题 4.9)

【实战】预测 4 天后的卫星位置 ------ 考虑 J2 摄动 (例题 4.9)

💡 摘要：地球不是完美的球体，它的"大肚子"（赤道隆起）会让卫星轨道发生进动。本文带你计算在 J2 摄动影响下，一颗卫星在飞行 4 天后的精确位置。

📚 1. 预备知识 (Prerequisites)

在开始之前，你需要了解：

[轨道六根数 (COE)]：描述轨道几何形状和位置的参数。
[J2 摄动] ：地球扁率对轨道的长期影响，主要导致升交点进动 (Ω˙\dot{\Omega}Ω˙) 和近地点幅角进动 (ω˙\dot{\omega}ω˙)。
[开普勒方程] ：连接时间（平近点角 MMM）和几何位置（偏近点角 EEE / 真近点角 θ\thetaθ）的超越方程。

🚀 2. 任务背景 (The Mission)

假设你正在追踪一颗卫星，你手头只有它现在的状态矢量（位置和速度）。如果这是一个理想的球体地球，你可以直接用二体模型外推。但现实是，地球是扁的！

这个微小的形状差异，在 4 天 (96小时) 的累积下，会让卫星的轨道平面旋转数度。如果忽略它，你的预测位置将偏离真实位置数百公里。

输入：初始状态 r0,v0\mathbf{r}_0, \mathbf{v}_0r0,v0。
时间：96 小时后。
模型：考虑 J2J_2J2 对 Ω\OmegaΩ 和 ω\omegaω 的影响。

🔮 3. 核心魔法：算法解读 (Algorithm Explanation)

我们要使用的魔法叫 "变分法" (Variation of Parameters) 的简化版 ------ 长期摄动法 (Secular Perturbation)。

3.1 通俗解读

这就好比你在旋转一个陀螺。

理想情况：陀螺直立旋转，轴线不动。
现实情况 ：由于重力（这里对应地球扁率），陀螺的轴线会慢慢画圈圈（进动）。
我们的算法就是：先算出这个"画圈圈"的速度，然后算出 4 天后轴线指到了哪里，最后再确定卫星在轨道上的具体位置。

3.2 流程图解

更新 Ω, ω, M
得到新 θ
初始状态 r0, v0

转为轨道根数 COE0 2. 计算摄动率 dΩ, dω 3. 时间推进 t -> t+96h 4. 求解开普勒方程 5. 转回状态矢量 rf, vf 最终预测结果

3.3 关键公式

J2 进动率 ：
Ω˙=−1.5nJ2(REp)2cos⁡i \dot{\Omega} = -1.5 n J_2 (\frac{R_E}{p})^2 \cos i Ω˙=−1.5nJ2(pRE)2cosi
ω˙=1.5nJ2(REp)2(2−2.5sin⁡2i) \dot{\omega} = 1.5 n J_2 (\frac{R_E}{p})^2 (2 - 2.5 \sin^2 i) ω˙=1.5nJ2(pRE)2(2−2.5sin2i)

开普勒方程 （这是最难啃的骨头）：
M=E−esin⁡E M = E - e \sin E M=E−esinE

给定 MMM 求 EEE，必须使用数值迭代（如牛顿法）。

💻 4. Python 代码实战 (Code Deep Dive)

4.1 关键片段一：从状态到根数

首先，我们需要知道卫星现在的轨道形状。

python 复制代码

coe0 = utils.rv2coe(r0_vec, v0_vec, mu)
# 得到 a, e, i, Omega, omega, theta

4.2 关键片段二：计算进动速度

利用 J2J_2J2 公式计算轨道平面的旋转速度。

python 复制代码

factor = 1.5 * n * J2 * (Re / p)**2
Omega_dot = -factor * math.cos(i0_rad)
omega_dot = factor * (2 - 2.5 * math.sin(i0_rad)**2)

注意单位：计算出的角速度通常是 rad/s，结果展示时可以转为 deg/day 直观感受。

4.3 关键片段三：开普勒方程求解器

因为我们要预测"未来"的位置，我们只能算出平近点角 MfM_fMf（它随时间线性增加）。要得到几何角度 θf\theta_fθf，必须解方程。

python 复制代码

def mean_anomaly_to_true_anomaly(M, e):
    # Newton-Raphson 迭代求解 M = E - e*sin(E)
    E = M if e < 0.8 else math.pi # 初始猜测
    for _ in range(50):
        f = E - e * math.sin(E) - M
        f_prime = 1 - e * math.cos(E)
        E -= f / f_prime
        if abs(f) < 1e-8: break
    # ... 再转为 theta

📊 5. 结果揭秘 (The Result)

运行脚本 solve_example_4_9.py：

text 复制代码

Initial Orbital Elements:
  a = 10643.6992 km
  e = 0.4261
  i = 39.6869 deg

Secular Rates:
  Omega_dot = -1.9066 deg/day
  omega_dot = 2.4293 deg/day

Final State Vector:
  rf = [9672.4434, 4320.4677, -8691.3647] km
  vf = [-3.0398, 3.3305, 0.6299] km/s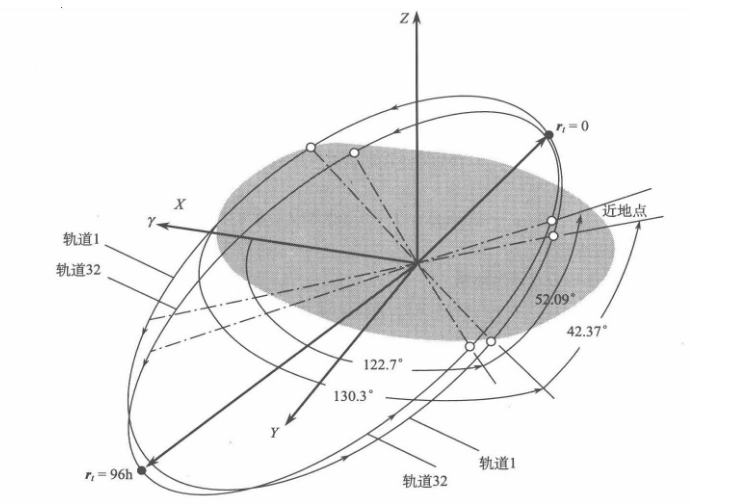

图：初始与最终位置矢量示意图

数据分析：

轨道进动 ：4 天内，轨道平面转动了近 8∘8^\circ8∘ (Ω\OmegaΩ)，近地点位置在轨道内移动了近 10∘10^\circ10∘ (ω\omegaω)。
精度提升：如果忽略这些变化，预测的位置误差将达到数千公里！这就是为什么简单的二体模型不能用于长期预报的原因。

📝 6. 总结

本例题展示了 分析法 (Analytical Method) 轨道预报的威力。相比于数值积分法（Cowell 法），这种方法计算极快，且能直观给出轨道参数的长期演化趋势，是任务设计初期的利器。