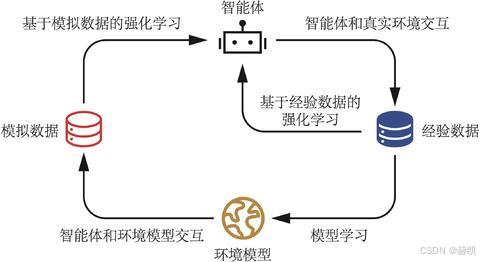
【强化学习】第六章 Dyna-Q 算法

Dyna-Q 算法

• Dyna-Q

Dyna-Q

采用 Q-planning 方法，结合真实数据与模型生成的模拟数据改进策略。Q-planning 通过选取曾访问过的状态和执行过的动作，依托模型获取转移后状态与奖励，再以 Q-learning 更新方式更新动作价值函数。

符号 / 术语	严谨定义
Q(s,a)	动作价值函数，代表在状态 s 执行动作 a 后，遵循当前策略获得的期望累积折扣回报。
M(s,a)	环境模型，存储状态 - 动作对 (s,a) 对应的转移结果：即时奖励 r 与下一状态 s'。
ε- 贪婪策略	平衡探索与利用的动作选择策略：以 1-ε 概率选择当前 Q(s,a) 最大的动作（利用已知最优），以 ε 概率随机选择动作（探索未知）。
α ∈ (0,1]	学习率，控制 Q 值更新的步长，值越小更新越平滑，值越大对新数据越敏感。
γ ∈ [0,1)	折扣因子，权衡即时奖励与未来奖励的权重，值越接近 1 代表越重视长期回报。
E, T, N	超参数：E 为总任务轮数（Episodes），T 为每轮任务的最大步数，N 为虚拟规划的次数。

记下来环境的规律：每次真实互动后，把 "在某个状态做某个动作，得到了什么奖励、去到了什么新状态" 记在一个 "环境模型" 里，相当于智能体自己画了一张 "环境规律地图"。

用地图做虚拟复盘：每次真实互动后，不是立刻继续试错，而是对着这张 "地图" 模拟走 N 次虚拟路线，用这些虚拟的 "试错经验" 提前优化自己的 "决策手册"（Q 表）。

我把它拆成 "初始化→多轮任务→单轮任务的每一步→真实互动→虚拟复盘→状态转移" 这几个环节，用文字一步步讲：

1. 初始化
   智能体先准备好两个 "手册"：
   决策手册（Q 表）：一开始是空的，所有状态 - 动作的 "预估奖励" 都设为 0。
   环境规律手册（环境模型 M）：一开始也是空的，还没记录任何环境的规律。
2. 多轮任务迭代
   智能体要完成 E 轮完整的任务（比如从起点走到终点算一轮），每一轮都从初始状态开始。
3. 单轮任务的每一步
   每一轮任务中，智能体最多走 T 步（或提前到达终点），每一步都包含 "真实互动" 和 "虚拟复盘" 两个阶段。
   • 阶段 1：真实环境互动（和 Q-learning 一样）
     选动作：智能体用 "ε- 贪婪" 的方式选动作 ------ 大部分时候选当前 "决策手册" 里预估奖励最高的动作（利用已知最优），偶尔随机选一个动作（探索新路线）。
     环境反馈：执行动作后，环境告诉智能体 "这次动作拿到了多少奖励，以及现在到了哪个新状态"。
     更新决策手册：智能体根据这次真实反馈，修正 "决策手册" 里对应状态 - 动作的预估奖励（让手册更准）。
     更新环境规律手册：智能体把这次真实互动的结果（状态→动作→奖励→新状态）记在 "环境规律手册" 里，相当于给 "地图" 补了一条新的规律。
   • 阶段 2：虚拟规划（Dyna-Q 独有的核心环节）
     选历史经验：从 "环境规律手册" 里随机挑一条过去的经验（比如 "在状态 s_m 做了动作 a_m"）。
     模拟虚拟互动：用 "环境规律手册" 里记录的规律，模拟出 "做这个动作会拿到多少奖励、去到哪个新状态"（相当于对着地图 "脑补" 了一次试错）。
     用虚拟经验更新决策手册：和真实互动时的规则一样，用这次虚拟的 "试错结果"，修正 "决策手册" 里对应状态 - 动作的预估奖励。
     重复虚拟复盘：上面这三步重复 N 次（N 是提前设定的次数），相当于智能体在 "脑子里" 模拟了 N 次试错，用这些虚拟经验让 "决策手册" 变得更准。
4. 状态转移
   把当前状态更新为真实互动后的新状态，准备进行下一步的真实互动。

import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm
import random
import time


class CliffWalkingEnv:
    def __init__(self, ncol, nrow):
        self.nrow = nrow
        self.ncol = ncol
        self.x = 0  # 记录当前智能体位置的横坐标
        self.y = self.nrow - 1  # 记录当前智能体位置的纵坐标

    def step(self, action):  # 外部调用这个函数来改变当前位置
        # 4种动作, change[0]:上, change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)
        # 定义在左上角
        change = [[0, -1], [0, 1], [-1, 0], [1, 0]]
        self.x = min(self.ncol - 1, max(0, self.x + change[action][0]))
        self.y = min(self.nrow - 1, max(0, self.y + change[action][1]))
        next_state = self.y * self.ncol + self.x
        reward = -1
        done = False
        if self.y == self.nrow - 1 and self.x > 0:  # 下一个位置在悬崖或者目标
            done = True
            if self.x != self.ncol - 1:
                reward = -100
        return next_state, reward, done

    def reset(self):  # 回归初始状态,起点在左上角
        self.x = 0
        self.y = self.nrow - 1
        return self.y * self.ncol + self.x

class DynaQ:
    """ Dyna-Q算法 """
    def __init__(self,
                 ncol,
                 nrow,
                 epsilon,
                 alpha,
                 gamma,
                 n_planning,
                 n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])  # 初始化Q(s,a)表格
        self.n_action = n_action  # 动作个数
        self.alpha = alpha  # 学习率
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略中的参数

        self.n_planning = n_planning  #执行Q-planning的次数, 对应1次Q-learning
        self.model = dict()  # 环境模型

    def take_action(self, state):  # 选取下一步的操作
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action

    def q_learning(self, s0, a0, r, s1):
        td_error = r + self.gamma * self.Q_table[s1].max(
        ) - self.Q_table[s0, a0]
        self.Q_table[s0, a0] += self.alpha * td_error

    def update(self, s0, a0, r, s1):
        self.q_learning(s0, a0, r, s1)
        self.model[(s0, a0)] = r, s1  # 将数据添加到模型中
        for _ in range(self.n_planning):  # Q-planning循环
            # 随机选择曾经遇到过的状态动作对
            (s, a), (r, s_) = random.choice(list(self.model.items()))
            self.q_learning(s, a, r, s_)

def DynaQ_CliffWalking(n_planning):
    ncol = 12
    nrow = 4
    env = CliffWalkingEnv(ncol, nrow)
    epsilon = 0.01
    alpha = 0.1
    gamma = 0.9
    agent = DynaQ(ncol, nrow, epsilon, alpha, gamma, n_planning)
    num_episodes = 300  # 智能体在环境中运行多少条序列

    return_list = []  # 记录每一条序列的回报
    for i in range(10):  # 显示10个进度条
        # tqdm的进度条功能
        with tqdm(total=int(num_episodes / 10),
                  desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):  # 每个进度条的序列数
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done = env.step(action)
                    episode_return += reward  # 这里回报的计算不进行折扣因子衰减
                    agent.update(state, action, reward, next_state)
                    state = next_state
                return_list.append(episode_return)
                if (i_episode + 1) % 10 == 0:  # 每10条序列打印一下这10条序列的平均回报
                    pbar.set_postfix({
                        'episode':
                        '%d' % (num_episodes / 10 * i + i_episode + 1),
                        'return':
                        '%.3f' % np.mean(return_list[-10:])
                    })
                pbar.update(1)
    return return_list

np.random.seed(0)
random.seed(0)
n_planning_list = [0, 2, 20]
for n_planning in n_planning_list:
    print('Q-planning步数为：%d' % n_planning)
    time.sleep(0.5)
    return_list = DynaQ_CliffWalking(n_planning)
    episodes_list = list(range(len(return_list)))
    plt.plot(episodes_list,
             return_list,
             label=str(n_planning) + ' planning steps')
plt.legend()
plt.xlabel('Episodes')
plt.ylabel('Returns')
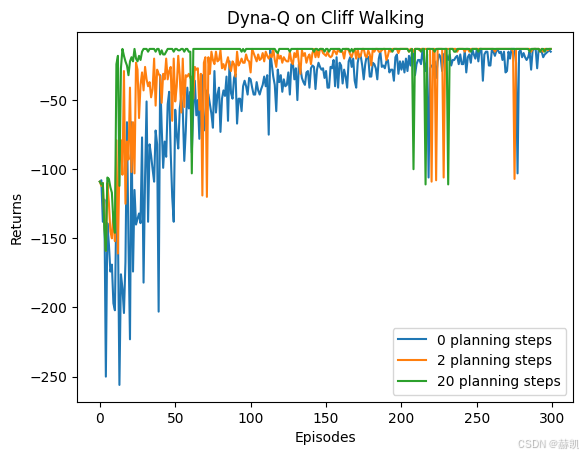
plt.title('Dyna-Q on {}'.format('Cliff Walking'))
plt.show()

Q-planning步数为：0

Iteration 0: 100%|██████████| 30/30 [00:00<00:00, 451.50it/s, episode=30, return=-138.400]

Iteration 1: 100%|██████████| 30/30 [00:00<00:00, 517.99it/s, episode=60, return=-64.100]

Iteration 2: 100%|██████████| 30/30 [00:00<00:00, 626.35it/s, episode=90, return=-46.000]

Iteration 3: 100%|██████████| 30/30 [00:00<00:00, 794.75it/s, episode=120, return=-38.000]

Iteration 4: 100%|██████████| 30/30 [00:00<00:00, 1056.89it/s, episode=150, return=-28.600]

Iteration 5: 100%|██████████| 30/30 [00:00<00:00, 1241.78it/s, episode=180, return=-25.300]

Iteration 6: 100%|██████████| 30/30 [00:00<00:00, 1515.72it/s, episode=210, return=-23.600]

Iteration 7: 100%|██████████| 30/30 [00:00<00:00, 1445.66it/s, episode=240, return=-20.100]

Iteration 8: 100%|██████████| 30/30 [00:00<00:00, 1919.71it/s, episode=270, return=-17.100]

Iteration 9: 100%|██████████| 30/30 [00:00<00:00, 1779.21it/s, episode=300, return=-16.500]

Q-planning步数为：2

Iteration 0: 100%|██████████| 30/30 [00:00<00:00, 174.59it/s, episode=30, return=-53.800]

Iteration 1: 100%|██████████| 30/30 [00:00<00:00, 613.01it/s, episode=60, return=-37.100]

Iteration 2: 100%|██████████| 30/30 [00:00<00:00, 816.68it/s, episode=90, return=-23.600]

Iteration 3: 100%|██████████| 30/30 [00:00<00:00, 591.19it/s, episode=120, return=-18.500]

Iteration 4: 100%|██████████| 30/30 [00:00<00:00, 624.28it/s, episode=150, return=-16.400]

Iteration 5: 100%|██████████| 30/30 [00:00<00:00, 620.82it/s, episode=180, return=-16.400]

Iteration 6: 100%|██████████| 30/30 [00:00<00:00, 696.69it/s, episode=210, return=-13.400]

Iteration 7: 100%|██████████| 30/30 [00:00<00:00, 1005.03it/s, episode=240, return=-13.200]

Iteration 8: 100%|██████████| 30/30 [00:00<00:00, 1236.94it/s, episode=270, return=-13.200]

Iteration 9: 100%|██████████| 30/30 [00:00<00:00, 1157.11it/s, episode=300, return=-13.500]

Q-planning步数为：20

Iteration 0: 100%|██████████| 30/30 [00:00<00:00, 132.47it/s, episode=30, return=-18.500]

Iteration 1: 100%|██████████| 30/30 [00:00<00:00, 286.26it/s, episode=60, return=-13.600]

Iteration 2: 100%|██████████| 30/30 [00:00<00:00, 267.86it/s, episode=90, return=-13.000]

Iteration 3: 100%|██████████| 30/30 [00:00<00:00, 195.62it/s, episode=120, return=-13.500]

Iteration 4: 100%|██████████| 30/30 [00:00<00:00, 296.15it/s, episode=150, return=-13.500]

Iteration 5: 100%|██████████| 30/30 [00:00<00:00, 305.62it/s, episode=180, return=-13.000]

Iteration 6: 100%|██████████| 30/30 [00:00<00:00, 316.29it/s, episode=210, return=-22.000]

Iteration 7: 100%|██████████| 30/30 [00:00<00:00, 290.45it/s, episode=240, return=-23.200]

Iteration 8: 100%|██████████| 30/30 [00:00<00:00, 301.22it/s, episode=270, return=-13.000]

Iteration 9: 100%|██████████| 30/30 [00:00<00:00, 288.04it/s, episode=300, return=-13.400]