矩阵束法(Matrix Pencil)用于 FMCW 雷达干扰抑制:论文精读
Wang J, Ding M, Yarovoy A. Matrix-pencil approach-based interference mitigation for FMCW radar systems[J]. IEEE Transactions on Microwave Theory and Techniques, 2021, 69(11): 5099-5115.
文章主线
这篇文章处理的是一个非常具体但又很普遍的工程难题:FMCW 雷达在一个 sweep 内得到的 beat 信号,本来应该是"若干个固定频率的正弦(复指数)叠加",但互扰/串扰/外部射频干扰会在某个时间段突然灌进来,使得这段采样完全不可用。如果你直接对带干扰的 beat 做 FFT 距离压缩,干扰能把噪声底抬到天上,弱目标完全被淹没,甚至会出现"鬼峰"。工程上最常用、也最稳的抑制方式是:先检测干扰发生的时间区间,把那段采样用窗口切掉(最简单就是置零),干扰没了,但同时你也切掉了那段"真实目标信号",于是距离像会出现能量损失、旁瓣变高、分辨率退化。
文章的核心思路是把"切掉造成的缺口"当成一个缺失数据重建问题来做,而且不是用插值,而是用物理/信号模型:在一次 sweep 内,目标 beat 可以写成复指数和
s~tar(t)=∑i=1M0aie−j2πfb,it \tilde s_{\text{tar}}(t)=\sum_{i=1}^{M_0} a_i e^{-j2\pi f_{b,i}t} s~tar(t)=i=1∑M0aie−j2πfb,it
离散后是
s[k]=∑i=1M0aizik,zi=ej2πfb,iΔt. s[k]=\sum_{i=1}^{M_0}a_i z_i^k,\quad z_i=e^{j2\pi f_{b,i}\Delta t}. s[k]=i=1∑M0aizik,zi=ej2πfb,iΔt.
因此"缺口"理论上也应当符合这组指数模型;只要能从缺口两侧的干净数据稳健估计出 {zi,ai}\{z_i,a_i\}{zi,ai},缺口内就能被模型补回。文章选择矩阵铅笔法(MP)来估计极点 ziz_izi,再用最小二乘估计系数 aia_iai,并引入一个"迭代融合"机制:每次先用模型补全缺口,再用真实数据把缺口两端"钉住",用这条变成连续的序列重新估计模型,反复迭代直到两端拟合误差不再下降。这个迭代在低 SNR、缺口很长时尤其关键,是其相对 Burg/IVM 的主要优势来源。
图 1:FMCW 处理链为什么自然导向"复指数模型"
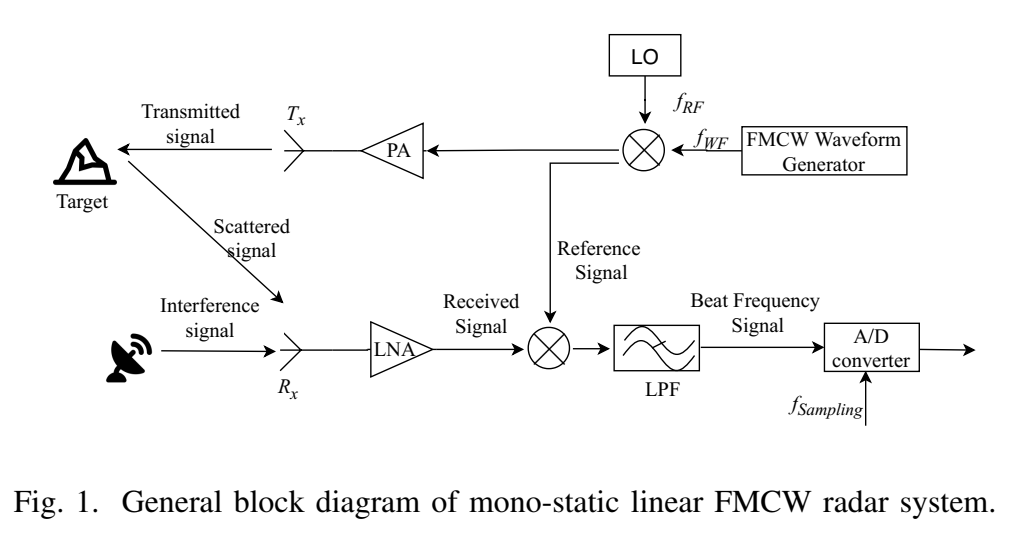
图 1 展示单站线性 FMCW:波形发生器 → 发射 → 目标散射/干扰叠加 → 接收 → 与参考信号混频(dechirp)→ 低通滤波(LPF)→ ADC 采样得到 beat 信号。关键点在于:dechirp 把"距离延迟"变成"固定 beat 频率",从而在一个 sweep 内,目标 beat 的数学形态非常接近"固定频率复指数之和"。这就是后面 MP 能用的根基。
一、从原文 (1)--(6) 出发推导 FMCW 的"复指数之和"
1. 发射信号的等价写法与瞬时频率
原文给出(式 (1))
p(t)=Atxexp(j2π(f0t+K2t2)),0≤t<T2. p(t)=A_{\mathrm{tx}}\exp\left(j2\pi\left(f_0 t+\frac{K}{2}t^2\right)\right),\quad 0\le t<\frac{T}{2}. p(t)=Atxexp(j2π(f0t+2Kt2)),0≤t<2T.
把括号展开成更常见的 LFM 形式:
p(t)=Atxexp{j2π(f0t+K2t2)}, p(t)=A_{\text{tx}}\exp\left\{j2\pi\left(f_0t+\frac{K}{2}t^2\right)\right\}, p(t)=Atxexp{j2π(f0t+2Kt2)},
其中 K=B/TK=B/TK=B/T 是扫频斜率(Hz/s)。
它的瞬时频率是相位对时间导数除以 2π2\pi2π:
finst(t)=12πddt(2π(f0t+K2t2))=f0+Kt, f_{\text{inst}}(t)=\frac{1}{2\pi}\frac{d}{dt}\left(2\pi\left(f_0t+\frac{K}{2}t^2\right)\right)=f_0+Kt, finst(t)=2π1dtd(2π(f0t+2Kt2))=f0+Kt,
这也解释了"线性扫频"的名字来源。
2. 目标回波:延迟版 chirp 的叠加(式 (2))
原文写(式 (2))
sr(t)=∑i=1MArx,iexp{j2π[f0(t−ti)+K2(t−ti)2]}, s_r(t)=\sum_{i=1}^{M}A_{\text{rx},i}\exp\left\{j2\pi\left[f_0(t-t_i)+\frac{K}{2}(t-t_i)^2\right]\right\}, sr(t)=i=1∑MArx,iexp{j2π[f0(t−ti)+2K(t−ti)2]},
其中 ti=2dict_i=\frac{2d_i}{c}ti=c2di。这一步把传播延迟完整地保留在相位里。
3. dechirp 的关键推导:乘 p∗(t)p^*(t)p∗(t) 后为什么出现固定 beat 频率
dechirp 的输出在无干扰情况下就是
s~(t)=Flp{sr(t)p∗(t)}. \tilde s(t)=\mathcal{F}_{\text{lp}}\{s_r(t)p^*(t)\}. s~(t)=Flp{sr(t)p∗(t)}.
取第 iii 个回波分量
sr,i(t)=Arx,iexp{j2π[f0(t−ti)+K2(t−ti)2]}. s_{r,i}(t)=A_{\text{rx},i}\exp\left\{j2\pi\left[f_0(t-t_i)+\frac{K}{2}(t-t_i)^2\right]\right\}. sr,i(t)=Arx,iexp{j2π[f0(t−ti)+2K(t−ti)2]}.
参考信号共轭
p∗(t)=Atxexp{−j2π(f0t+K2t2)}. p^*(t)=A_{\text{tx}}\exp\left\{-j2\pi\left(f_0t+\frac{K}{2}t^2\right)\right\}. p∗(t)=Atxexp{−j2π(f0t+2Kt2)}.
相乘得到
sr,i(t)p∗(t)=AtxArx,iexp{j2πΨi(t)}, s_{r,i}(t)p^*(t)=A_{\text{tx}}A_{\text{rx},i}\exp\{j2\pi\Psi_i(t)\}, sr,i(t)p∗(t)=AtxArx,iexp{j2πΨi(t)},
其中
Ψi(t)=[f0(t−ti)+K2(t−ti)2]−[f0t+K2t2]. \Psi_i(t)=\left[f_0(t-t_i)+\frac{K}{2}(t-t_i)^2\right]-\left[f_0t+\frac{K}{2}t^2\right]. Ψi(t)=[f0(t−ti)+2K(t−ti)2]−[f0t+2Kt2].
展开 (t−ti)2=t2−2tti+ti2(t-t_i)^2=t^2-2tt_i+t_i^2(t−ti)2=t2−2tti+ti2:
Ψi(t)=f0t−f0ti+K2(t2−2tti+ti2)−f0t−K2t2=−f0ti−Ktti+K2ti2. \Psi_i(t)=f_0t-f_0t_i+\frac{K}{2}(t^2-2tt_i+t_i^2)-f_0t-\frac{K}{2}t^2 =-f_0t_i-Ktt_i+\frac{K}{2}t_i^2. Ψi(t)=f0t−f0ti+2K(t2−2tti+ti2)−f0t−2Kt2=−f0ti−Ktti+2Kti2.
于是
sr,i(t)p∗(t)=AtxArx,iexp{j2π(−f0ti+K2ti2)}⋅exp{−j2π(Kti)t}. s_{r,i}(t)p^*(t)=A_{\text{tx}}A_{\text{rx},i}\exp\left\{j2\pi\left(-f_0t_i+\frac{K}{2}t_i^2\right)\right\}\cdot \exp\left\{-j2\pi(Kt_i)t\right\}. sr,i(t)p∗(t)=AtxArx,iexp{j2π(−f0ti+2Kti2)}⋅exp{−j2π(Kti)t}.
第一个指数项与 ttt 无关,是常相位,可并入复幅度;第二个指数项是一个固定频率的复指数,频率为
fb,i=Kti. f_{b,i}=Kt_i. fb,i=Kti.
因此 dechirp+LPF 后目标项就是"复指数之和"(原文式 (4) 的目标部分):
s~tar(t)=∑i=1M0aie−j2πfb,it. \tilde s_{\text{tar}}(t)=\sum_{i=1}^{M_0}a_i e^{-j2\pi f_{b,i}t}. s~tar(t)=i=1∑M0aie−j2πfb,it.
这里
ai=AtxArx,iexp{j2π(−f0ti+K2ti2)}. a_i=A_{\text{tx}}A_{\text{rx},i}\exp\left\{j2\pi\left(-f_0t_i+\frac{K}{2}t_i^2\right)\right\}. ai=AtxArx,iexp{j2π(−f0ti+2Kti2)}.
这正是原文 (3)--(4) 中"把常相位项吸收到幅度里"的那一步。
4. 距离映射(式 (5))
用 ti=2dict_i=\frac{2d_i}{c}ti=c2di,得到(式 (5))
di=c fb,i2K. d_i=\frac{c\,f_{b,i}}{2K}. di=2Kcfb,i.
所以"找 beat 频率峰值"就等价于"测距离"。
5. 完整测量模型(式 (6)):目标 + 干扰 + 噪声
原文(式 (6))将实际测量写成
s(t)=s~tar(t)+s~int(t)+n(t). s(t)=\tilde s_{\text{tar}}(t)+\tilde s_{\text{int}}(t)+n(t). s(t)=s~tar(t)+s~int(t)+n(t).
到这里,已经把后续算法需要的两个结构点讲清楚了:目标在一个 sweep 内近似"定频复指数和";很多干扰在 dechirp 后表现出"非定频、局部出现"的结构差异。
二、图 2:四类干扰为何"时间域局部出现"是普遍现象
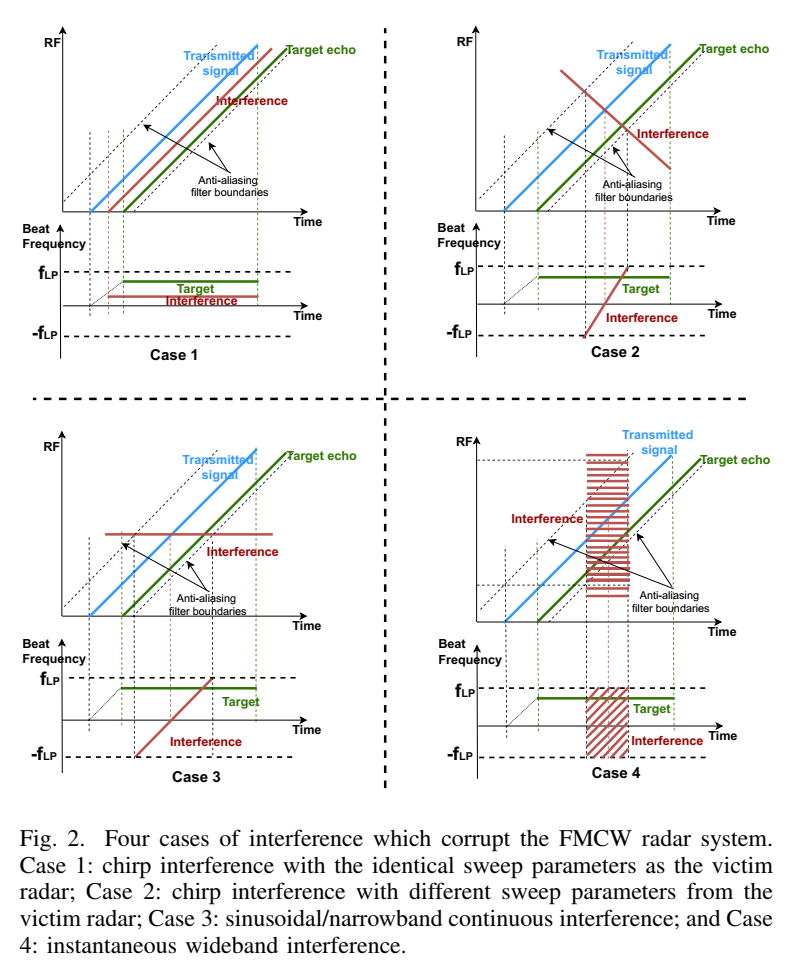
图 2 把干扰分四类,其中 Case 2/3/4 都有一个共同的工程事实:干扰 dechirp 后的 beat 频率是随时间变化的直线(chirp-like),而接收链有低通/抗混叠滤波器,只有其瞬时频率落入 [−fLP, fLP][ -f_{\text{LP}},\,f_{\text{LP}}][−fLP,fLP] 的那段才会出现在 ADC 输出里,因此表现为短时间"污染片段"。文章主要以 Case 2(斜率不同的 FMCW 干扰)为代表来推导。
下面把"短时间"的持续长度用一个简单不等式推出来(从式 (11) 自然推出):
给出干扰 dechirp 后的瞬时 beat 频率(式 (11))
fb,I(t)=K1t+K2,K1=K−KI. f_{b,I}(t)=K_1 t+K_2,\quad K_1=K-K_I. fb,I(t)=K1t+K2,K1=K−KI.
低通通过条件可写成
∣fb,I(t)∣≤fLP. |f_{b,I}(t)|\le f_{\text{LP}}. ∣fb,I(t)∣≤fLP.
于是
−fLP≤K1t+K2≤fLP. -f_{\text{LP}}\le K_1 t+K_2\le f_{\text{LP}}. −fLP≤K1t+K2≤fLP.
当 K1≠0K_1\neq 0K1=0 时,这给出一段时间区间;其长度(持续时间)为
Δtint=2fLP∣K1∣=2fLP∣K−KI∣. \Delta t_{\text{int}}=\frac{2f_{\text{LP}}}{|K_1|}=\frac{2f_{\text{LP}}}{|K-K_I|}. Δtint=∣K1∣2fLP=∣K−KI∣2fLP.
这说明:斜率差越大,干扰落入低通带内的时间越短;斜率差越小(极端接近),Δtint\Delta t_{\text{int}}Δtint 变长,甚至可能污染整个 sweep,原文也明确说这种极端情形下本方法不适用。
三、 (7)--(11) 的干扰推导:把"chirp-like"结构算出来
1. 干扰信号模型(式 (7))
假设干扰雷达与受害雷达相距 dId_IdI,干扰到达接收端为(式 (7))
sint(t)=AIexp{j2π[fI,0(t−tI)+KI2(t−tI)2]}, s_{\text{int}}(t)=A_I\exp\left\{j2\pi\left[f_{I,0}(t-t_I)+\frac{K_I}{2}(t-t_I)^2\right]\right\}, sint(t)=AIexp{j2π[fI,0(t−tI)+2KI(t−tI)2]},
其中 tI=dI/ct_I=d_I/ctI=dI/c,KI=BI/TIK_I=B_I/T_IKI=BI/TI。
2. dechirp 后的相位差:为什么会有 t2t^2t2 项
与 p∗(t)p^*(t)p∗(t) 相乘:
sint(t)p∗(t)=AIAtxexp{j2πΘ(t)}, s_{\text{int}}(t)p^*(t)=A_I A_{\text{tx}}\exp\{j2\pi\Theta(t)\}, sint(t)p∗(t)=AIAtxexp{j2πΘ(t)},
其中
Θ(t)=[fI,0(t−tI)+KI2(t−tI)2]−[f0t+K2t2]. \Theta(t)=\left[f_{I,0}(t-t_I)+\frac{K_I}{2}(t-t_I)^2\right]-\left[f_0t+\frac{K}{2}t^2\right]. Θ(t)=[fI,0(t−tI)+2KI(t−tI)2]−[f0t+2Kt2].
展开得到
Θ(t)=(KI2−K2)t2+(fI,0−f0−KItI)t+(KI2tI2−fI,0tI). \Theta(t)=\left(\frac{K_I}{2}-\frac{K}{2}\right)t^2+\bigl(f_{I,0}-f_0-K_I t_I\bigr)t+\left(\frac{K_I}{2}t_I^2-f_{I,0}t_I\right). Θ(t)=(2KI−2K)t2+(fI,0−f0−KItI)t+(2KItI2−fI,0tI).
把与 ttt 无关的常相位并入复幅度
aI=AIAtxexp{j2π(KI2tI2−fI,0tI)} a_I=A_I A_{\text{tx}}\exp\left\{j2\pi\left(\frac{K_I}{2}t_I^2-f_{I,0}t_I\right)\right\} aI=AIAtxexp{j2π(2KItI2−fI,0tI)}
并令
Φ(t)=2π[(KI2−K2)t2+(fI,0−f0−KItI)t], \Phi(t)=2\pi\left[\left(\frac{K_I}{2}-\frac{K}{2}\right)t^2+\bigl(f_{I,0}-f_0-K_I t_I\bigr)t\right], Φ(t)=2π[(2KI−2K)t2+(fI,0−f0−KItI)t],
就得到式 (8)--(10):
s~int(t)=Flp{aIejΦ(t)}. \tilde s_{\text{int}}(t)=\mathcal{F}_{\text{lp}}\{a_I e^{j\Phi(t)}\}. s~int(t)=Flp{aIejΦ(t)}.
它的结构与目标项的最大差异在于:只要 KI≠KK_I\neq KKI=K,Φ(t)\Phi(t)Φ(t) 中就必然有二次项 t2t^2t2,这意味着瞬时频率随时间变化。
3. 瞬时 beat 频率(式 (11))
定义(式 (11))
fb,I(t)=−12π∂Φ(t)∂t=K1t+K2, f_{b,I}(t)=-\frac{1}{2\pi}\frac{\partial \Phi(t)}{\partial t}=K_1 t+K_2, fb,I(t)=−2π1∂t∂Φ(t)=K1t+K2,
其中
K1=K−KI,K2=f0−fI,0+KItI. K_1=K-K_I,\quad K_2=f_0-f_{I,0}+K_I t_I. K1=K−KI,K2=f0−fI,0+KItI.
这条线性规律与前面"低通限定导致短时出现"的解释正好连贯。
四、图 3:方法流程 ------"切掉 + 重建"为什么被作者称为 signal fusion
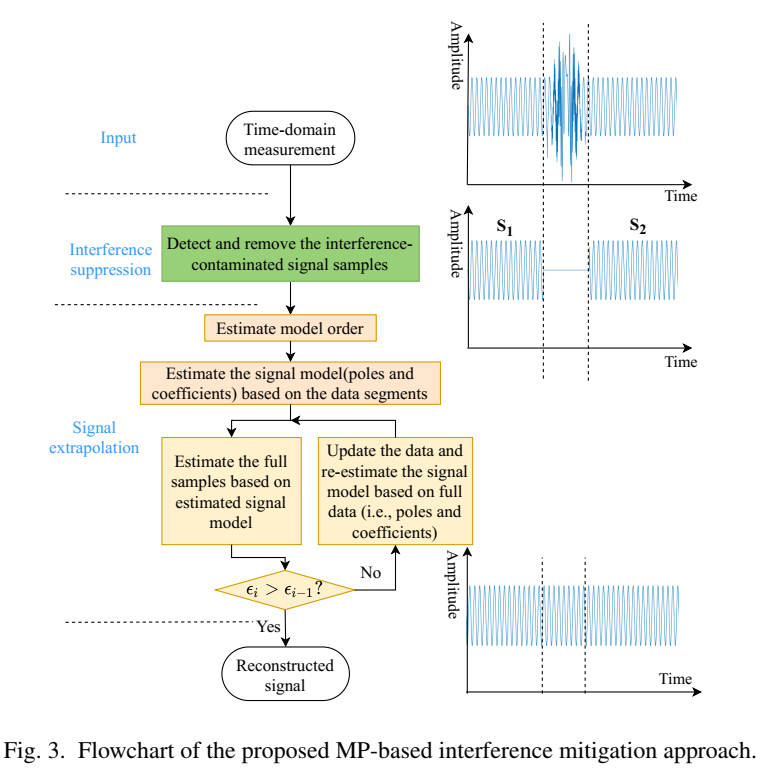
图 3 的右侧画出"干扰切掉后形成缺口"的两段信号 S1,S2S_1,S_2S1,S2。作者把后续重建称为"signal fusion",理由在于:你手头不再是一条连续序列,而是两个(或多个)彼此分离的观测片段;要恢复缺口,本质是在统一的物理模型约束下,把不同片段的信息融合成一条一致的全序列。与多频段成像的"融合"不同,这里不需要做段间不相干校正(incoherence correction),因为它们来自同一次 sweep、同一个本振参考,缺口只是时间上缺样本。
五、离散模型与切割记号((12)--(14)):把"缺口"写成可解的线性代数问题
1. 离散化(式 (12))
s[k]=∑i=1M0aizik+s~int[k]+n[k],k=0,...,N−1, s[k]=\sum_{i=1}^{M_0}a_i z_i^k+\tilde s_{\text{int}}[k]+n[k],\quad k=0,\dots,N-1, s[k]=i=1∑M0aizik+s~int[k]+n[k],k=0,...,N−1,
其中
zi=ej2πfb,iΔt. z_i=e^{j2\pi f_{b,i}\Delta t}. zi=ej2πfb,iΔt.
目标项在离散域仍是复指数和,这是后续 Hankel 低秩结构成立的前提。
2. 干扰切割后两段数据(式 (13)--(14))
检测到污染区间 [N1,N2][N_1,N_2][N1,N2] 后,切掉该区间后,认为剩余观测满足
s[k]=∑i=1M0aizik+n[k],k∈[0,N1−1]∪[N2+1,N−1]. s[k]=\sum_{i=1}^{M_0}a_i z_i^k+n[k],\quad k\in[0,N_1-1]\cup[N_2+1,N-1]. s[k]=i=1∑M0aizik+n[k],k∈[0,N1−1]∪[N2+1,N−1].
定义两段信号(原文式 (14))
s1[k]=s[k],k=0,...,N1−1, s_1[k]=s[k],\quad k=0,\dots,N_1-1, s1[k]=s[k],k=0,...,N1−1,
s2[k]=s[k+N2+1],k=0,...,N−N2−2. s_2[k]=s[k+N_2+1],\quad k=0,\dots,N-N_2-2. s2[k]=s[k+N2+1],k=0,...,N−N2−2.
这里最容易被忽略、但对重建极其关键的是:s2s_2s2 的索引虽然从 0 开始,但它对应原序列的时间幂次是 k=N2+1,...,N−1k=N_2+1,\dots,N-1k=N2+1,...,N−1,因此后面拟合 Vandermonde 矩阵时必须把指数幂次对齐。
六、矩阵铅笔法在本文中的核心:从 (15)--(22) 把"极点估计"做成稳健的特征值问题
这一部分给出了构造方式与最终特征方程(式 (22))
1. 不连续样本的 Hankel 构造(式 (15)--(17))
对每一段 sis_isi(i=1,2i=1,2i=1,2),构造两块 Hankel 矩阵(式 (15))
Hi0=[D0i,D1i,...,DL−1i],Hi1=[D1i,D2i,...,DLi], H_{i0}=[D^{i}{0},D^{i}{1},\dots,D^{i}{L-1}],\qquad H{i1}=[D^{i}{1},D^{i}{2},\dots,D^{i}_{L}], Hi0=[D0i,D1i,...,DL−1i],Hi1=[D1i,D2i,...,DLi],
列向量(式 (16))
Dki=[si[k],si[k+1],...,si[Mi−L−1+k]]T, D^{i}_{k}=\bigl[s_i[k],s_i[k+1],\dots,s_i[M_i-L-1+k]\bigr]^T, Dki=[si[k],si[k+1],...,si[Mi−L−1+k]]T,
其中 M1=N1, M2=N−N2−1M_1=N_1,\;M_2=N-N_2-1M1=N1,M2=N−N2−1。参数 LLL 满足
M^0<L<min { M1−M^0, M2−M^0 }. \hat{M}_0 < L < \min\!\left\{\, M_1 - \hat{M}_0,\; M_2 - \hat{M}_0 \,\right\}. M^0<L<min{M1−M^0,M2−M^0}.
然后把两段的 Hankel 矩阵竖向堆叠(式 (17)):
X0=[H10H20],X1=[H11H21]. X_0=\begin{bmatrix}H_{10}\\H_{20}\end{bmatrix},\qquad X_1=\begin{bmatrix}H_{11}\\H_{21}\end{bmatrix}. X0=[H10H20],X1=[H11H21].
直觉上,这是在告诉算法:虽然数据断开了,但两段共享同一组极点 {zi}\{z_i\}{zi},应该在统一模型下共同估计。
2. 用截断 SVD 提取信号子空间(式 (18)--(21))
对 X0,X1X_0,X_1X0,X1 做 SVD(式 (18)--(19))并截断(式 (20)--(21)):
X0≈U0Σ0,M^0V0H,X1≈U1Σ1,M^0V1H. X_0\approx U_0\Sigma_{0,\hat M_0}V_0^H,\qquad X_1\approx U_1\Sigma_{1,\hat M_0}V_1^H. X0≈U0Σ0,M^0V0H,X1≈U1Σ1,M^0V1H.
这一步的意义是:理想无噪声时,Hankel 矩阵由 M0M_0M0 个指数生成,秩不超过 M0M_0M0;有噪声时秩被"抬满",但主奇异值对应的子空间仍主要由信号贡献,截断等价于把估计限制在信号子空间上,从而稳定后续求特征值。
3. 从广义特征值到普通特征值(式 (22) 的"等价性")
作者最终写到(式 (22))
det (Σ0,M^0−1U0HU1Σ1,M^0V1HV0−λI)=0, \det\!\left(\Sigma^{-1}{0,\hat M_0}U_0^HU_1\Sigma{1,\hat M_0}V_1^HV_0-\lambda I\right)=0, det(Σ0,M^0−1U0HU1Σ1,M^0V1HV0−λI)=0,
其根 λi\lambda_iλi 即估计极点 z^i=λi\hat z_i=\lambda_iz^i=λi。
这一式在正文里像"跳步"一样出现;具体推导在附录 B 里,核心就是把
X1v=λX0v X_1v=\lambda X_0v X1v=λX0v
投影到 X0X_0X0 的信号子空间上,并用截断 SVD 把问题降到 M^0\hat M_0M^0 维。
七、系数估计与缺口重建:从 (23)--(28) 出发,"为什么迭代融合能明显提升长缺口/低 SNR 表现"
1. 系数的最小二乘(式 (23))
原文把系数估计写成 m=Zam=Zam=Za 的最小二乘问题(式 (23))。把它写得更"可计算"一点:
设观测向量
m=[s1[0]⋮s1[N1−1]s2[0]⋮s2[N−N2−2]], m=\begin{bmatrix}s_1[0]\\ \vdots\\ s_1[N_1-1]\\ s_2[0]\\ \vdots\\ s_2[N-N_2-2]\end{bmatrix}, m= s1[0]⋮s1[N1−1]s2[0]⋮s2[N−N2−2] ,
构造 Vandermonde 型矩阵 ZZZ,其行对应原始时间索引幂次
Z=[z10z20⋯zM^00⋮⋮⋮z1N1−1z2N1−1⋯zM^0N1−1z1N2+1z2N2+1⋯zM^0N2+1⋮⋮⋮z1N−1z2N−1⋯zM^0N−1]. Z=\begin{bmatrix} z_1^0 & z_2^0 & \cdots & z_{\hat M_0}^0\\ \vdots & \vdots & & \vdots\\ z_1^{N_1-1} & z_2^{N_1-1} & \cdots & z_{\hat M_0}^{N_1-1}\\ z_1^{N_2+1} & z_2^{N_2+1} & \cdots & z_{\hat M_0}^{N_2+1}\\ \vdots & \vdots & & \vdots\\ z_1^{N-1} & z_2^{N-1} & \cdots & z_{\hat M_0}^{N-1} \end{bmatrix}. Z= z10⋮z1N1−1z1N2+1⋮z1N−1z20⋮z2N1−1z2N2+1⋮z2N−1⋯⋯⋯⋯zM^00⋮zM^0N1−1zM^0N2+1⋮zM^0N−1 .
则最小二乘解为
a^=argmina∥Za−m∥22=(ZHZ)−1ZHm, \hat a=\arg\min_a\|Za-m\|_2^2 =(Z^HZ)^{-1}Z^Hm, a^=argamin∥Za−m∥22=(ZHZ)−1ZHm,
或更稳健地用 QR/SVD 解。写式 (23) 的目的就是强调:第二段 s2s_2s2 的幂次从 N2+1N_2+1N2+1 开始,而不是从 0 开始。
2. 用模型生成全序列(式 (24)--(25))
得到 {z^i,a^i}\{\hat z_i,\hat a_i\}{z^i,a^i} 后(式 (24)):
s^[k]=∑i=1M^0a^iz^ik,k=0,...,N−1. \hat s[k]=\sum_{i=1}^{\hat M_0}\hat a_i\hat z_i^k,\quad k=0,\dots,N-1. s^[k]=i=1∑M^0a^iz^ik,k=0,...,N−1.
作者进一步把它拆成三段(式 (25)):前段 s^1\hat s_1s^1、缺口段 s^g\hat s_gs^g、后段 s^2\hat s_2s^2。
3. "融合替换"一步(式 (26)):只让模型负责缺口,让真实数据负责两端
式 (26) 做了一个非常关键的操作:把 s^\hat ss^ 的前后两段替换回真实测量的 s1,s2s_1,s_2s1,s2,只保留缺口段为模型生成值:
s^[k]={s1[k],k∈[0,N1−1],s^g[k−N1],k∈[N1,N2],s2[k−N2−1],k∈[N2+1,N−1]. \hat s[k]= \begin{cases} s_1[k], & k\in[0,N_1-1],\\ \hat s_g[k-N_1], & k\in[N_1,N_2],\\ s_2[k-N_2-1], & k\in[N_2+1,N-1]. \end{cases} s^[k]=⎩ ⎨ ⎧s1[k],s^g[k−N1],s2[k−N2−1],k∈[0,N1−1],k∈[N1,N2],k∈[N2+1,N−1].
这一招的意义可以用"误差来源"来解释:初次估计 z^i\hat z_iz^i 时用的是不连续样本,噪声与断裂会使极点估计有偏;一旦极点稍有偏差,用 ∑a^iz^ik\sum \hat a_i\hat z_i^k∑a^iz^ik 生成的前后段就会出现缓慢的相位漂移/幅度漂移。替换回真实 s1,s2s_1,s_2s1,s2 等价于在缺口两侧加了硬约束:模型必须与真实观测一致,否则迭代时误差就会反映出来。
4. 迭代停止准则(式 (27)--(28))的更直观解释
原文用两侧误差的 l2l_2l2 范数(式 (27))
εi=∥s^1(i)−s1∥2+∥s^2(i)−s2∥2 \varepsilon_i=\|\hat s^{(i)}_1-s_1\|_2+\|\hat s^{(i)}_2-s_2\|_2 εi=∥s^1(i)−s1∥2+∥s^2(i)−s2∥2
并在(式 (28))当误差不再下降时停止。这个准则从统计角度可以理解为一种"避免过拟合噪声"的简单早停:如果继续迭代反而让两侧匹配变差,通常说明新一轮的极点/系数开始把噪声也当作指数成分去拟合,从而破坏真实结构,于是应该停止。
八、仿真部分
1. 点目标仿真:Fig.4--Fig.5 在验证"统一模型 + 双侧共同约束"的价值
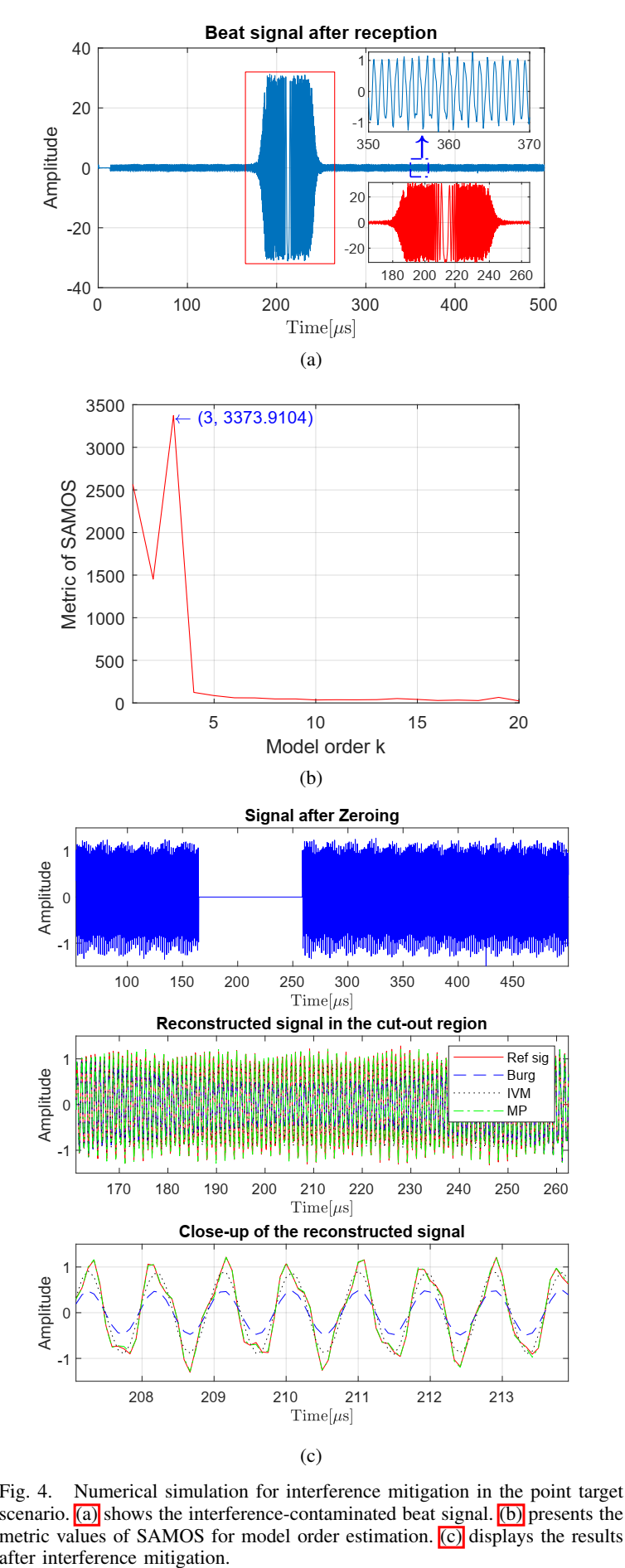
Fig.4(a) 给出干扰污染的 beat 信号,污染段 165--265 µs 呈现明显 chirp-like;右上角放大无干扰区域能看出目标项由多正弦叠加组成。Fig.4(b) 中 SAMOS 选择模型阶数为 3,与三目标一致。Fig.4© 对比缺口重建:零填产生断裂;Burg/IVM/MP 都能补,但 MP 在缺口内部的相位连续性与幅度更贴合参考,这一点在底部 close-up 里最明显。
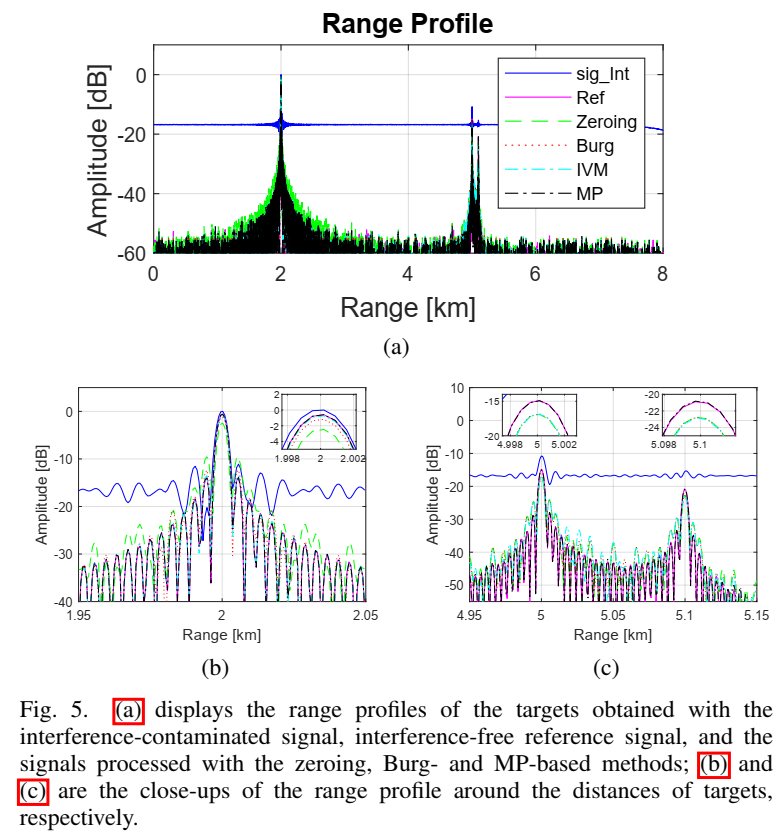
Fig.5 把时域信号做 FFT 距离压缩后对比:零填的旁瓣抬高、主瓣下降;Burg/IVM 在近距离强目标附近还行,但对远距离弱目标的能量恢复较差;MP 在主瓣高度与旁瓣结构上更接近参考,文章给出了 RSNR 与相关系数的定量优势(例如 MP 的 RSNR 明显更高,相关系数更接近 1)。这里背后的原因并不是"MP 比较神奇",而是缺口越大时,Burg/IVM 的前向/后向外推误差会累积并在缺口中部最大,而 MP 的全局指数模型是同时由两侧共同约束的。
2. 扩展目标仿真:Fig.6--Fig.7 在验证"阶数选择困难时 MP 仍更稳",并展示 IVM 的不稳定
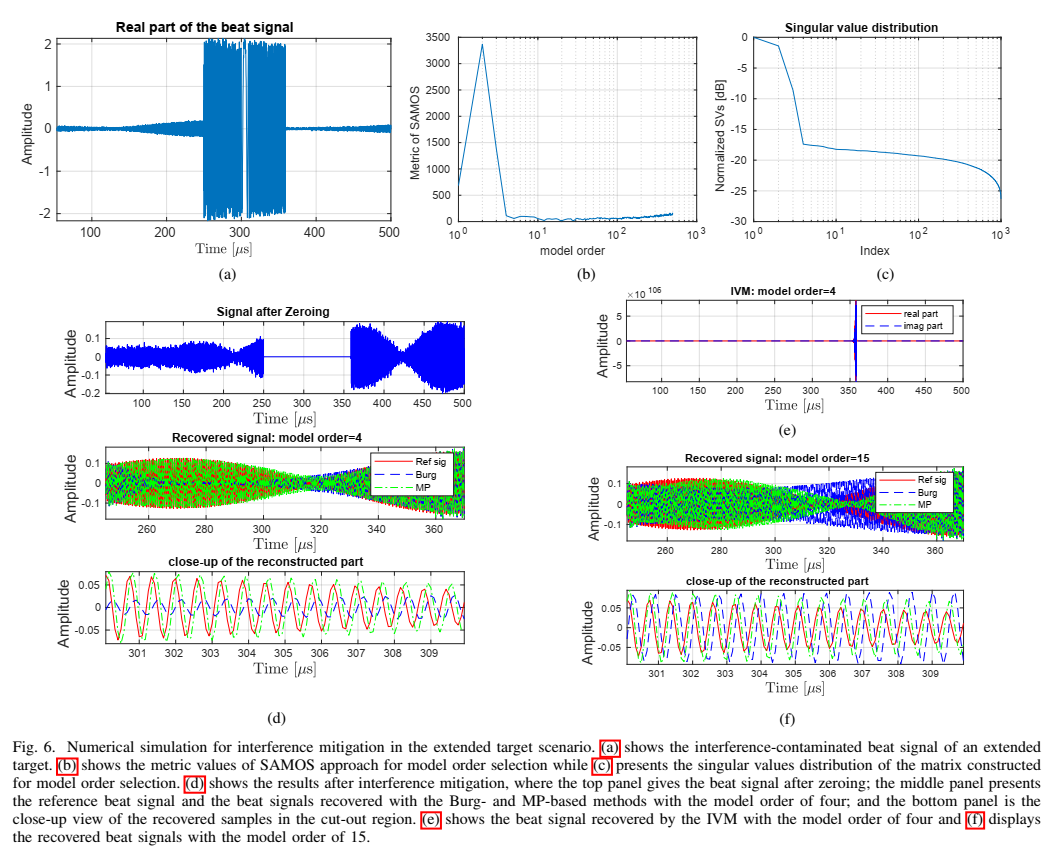
扩展目标由 15 个近邻散射点组成,间距小于距离分辨率,因此 beat 频率高度相关。Fig.6(b) 显示 SAMOS 误判阶数为 2;Fig.6© 的奇异值分布提示至少不应小于 4,于是作者用经验阈值定阶。Fig.6(e) 中 IVM 出现 blow-up(爆振),说明其在该设置下数值稳定性不足。Fig.6(d)(f) 的 close-up 显示 MP 在缺口段的形状更贴近参考。
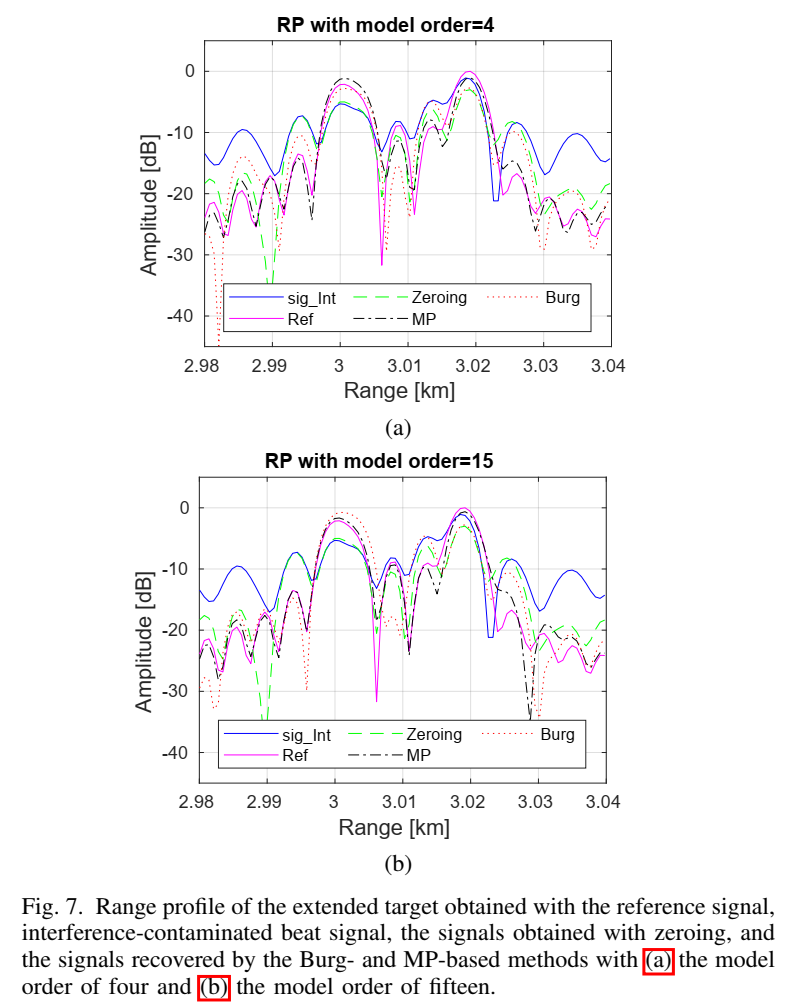
Fig.7 的距离像进一步把这种差异落实到可检测性:MP 的距离像更接近参考,Burg 更易出现形态偏差。作者还讨论了一个细节:在某些"根非常密集"的极端情况下,Burg 可能偶尔更好,因为它是在 AR 多项式系数上做估计,而 MP 倾向于在均方意义下选取若干主导正弦根;当根极其密集时,两者的数值敏感性不同。
3. 干扰持续时间与 SNR:Fig.8 在验证"缺口越长越需要迭代融合"的结论
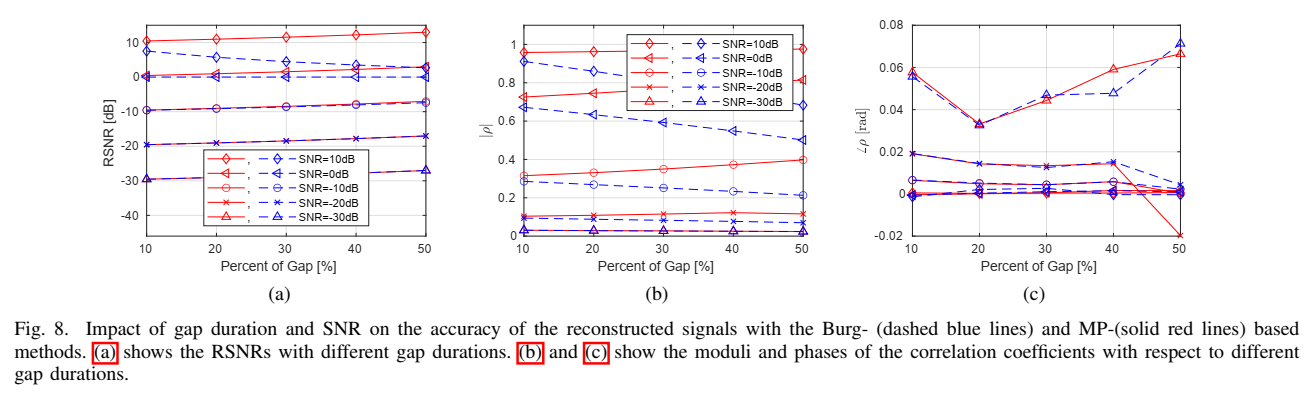
Fig.8(a)--© 给出统计结果:当 SNR<0 dB 时,两者 RSNR 相近;当 SNR≥0 dB 且缺口加宽时,MP 的 RSNR 仍能提升,而 Burg 易持平甚至下降。作者给了一个非常实用的解释:切除操作同时切掉干扰段内的噪声与信号。当 SNR<0 dB 时,切掉的"主要是噪声能量",即使补得一般也可能得到 RSNR 提升;当 SNR≥0 dB 时,切掉的"主要是信号能量",这时只有能把缺口内信号结构补得足够准的方法(MP 的统一模型 + 迭代)才能真正恢复性能。
九、实验部分
1. 实验设置:PARSAX 全极化 FMCW(Fig.9 + Table II)

实验使用 TU Delft 的 PARSAX S 波段全极化 FMCW 雷达。关键设置是:H 极化发上扫、V 极化发下扫,同时接收全极化回波;这样 HV 通道会被 VV 的强信号串扰污染,这种污染在原文分类里属于 Fig.2 的 Case 2(斜率不同导致局部污染)。
表 II 给出的关键参数是:中心频率 3.1315 GHz、带宽 40 MHz、sweep 1 ms、每 sweep 采样 16384、最大距离 18.75 km、每 CPI 512 sweep。
2. 实验 1:烟囱目标(Fig.10--Fig.11)验证"缺口补全能把弱峰救回来"
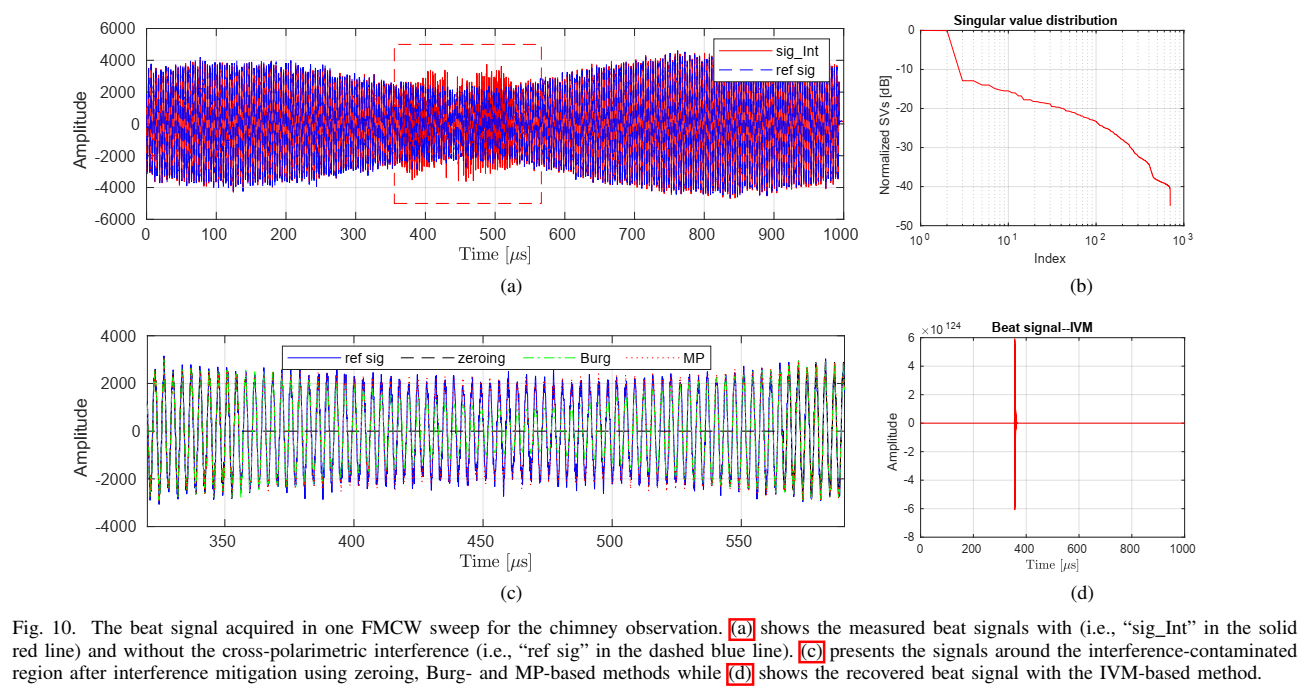
Fig.10(a) 叠加展示受干扰的 HV beat 与参考 HV beat(参考由单独 H 上扫获得)。Fig.10(b) 给出奇异值分布,作者指出 SAMOS 选阶严重低估,因此采用经验阈值(如归一化奇异值阈值 10−210^{-2}10−2)选得阶数 40。Fig.10© 展示缺口附近的重建:Burg 在缺口段幅度偏低,MP 更贴近参考;Fig.10(d) 仍能看到 IVM 的 blow-up。
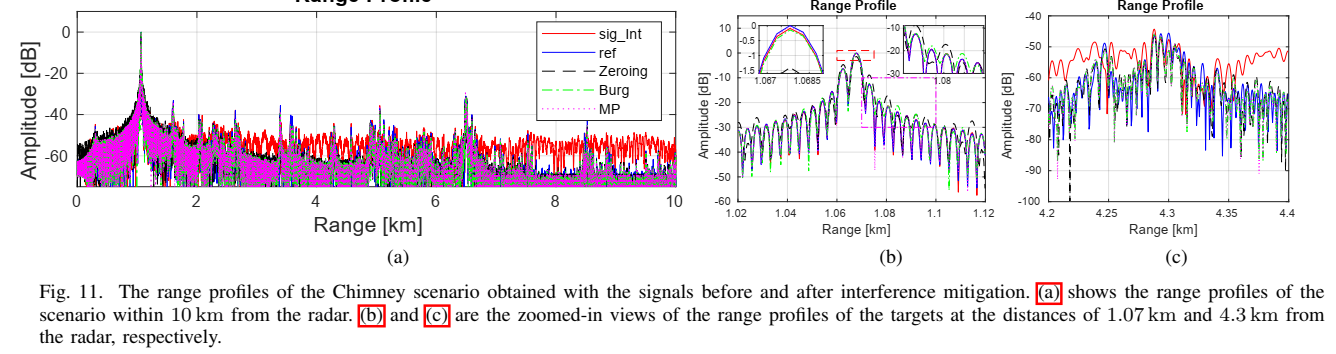
Fig.11 的距离像说明两件事:第一,带干扰的距离像噪声底更高,会遮蔽弱目标;第二,MP 抑制 + 重建后,距离像与参考更一致,并能在约 4.24 km 处恢复清晰峰值,而带干扰信号在相同位置甚至出现深陷(原文解释可能是干扰与目标相消导致的 destructive interference)。
3. 实验 2:雨滴分布目标(Fig.12--Fig.14)验证"先慢时间 FFT 再逐多普勒 bin 抑制"的策略
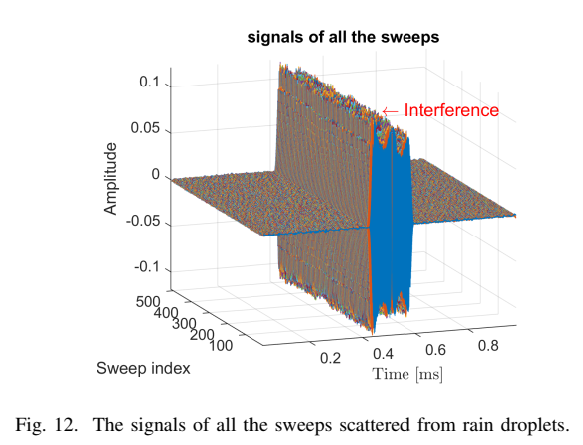
Fig.12 把 512 个 sweep 的 HV 数据堆叠显示,干扰集中在 0.4--0.6 ms,且幅度远大于雨滴 HV 回波。直接做 R-D 会被完全淹没。
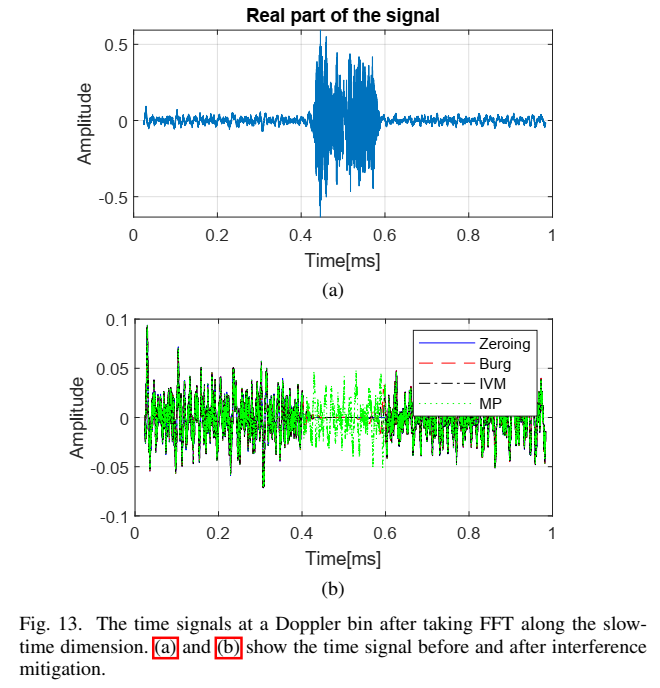
作者提出先沿慢时间做 FFT,得到每个 Doppler bin 的快时间信号,再对每个 Doppler bin 做干扰抑制与缺口重建,以避免重建误差对多普勒估计的累积影响。Fig.13(b) 显示 MP 能把缺口补得更完整,而 Burg/IVM 更像"只在缺口两端补一点",中间明显低估。
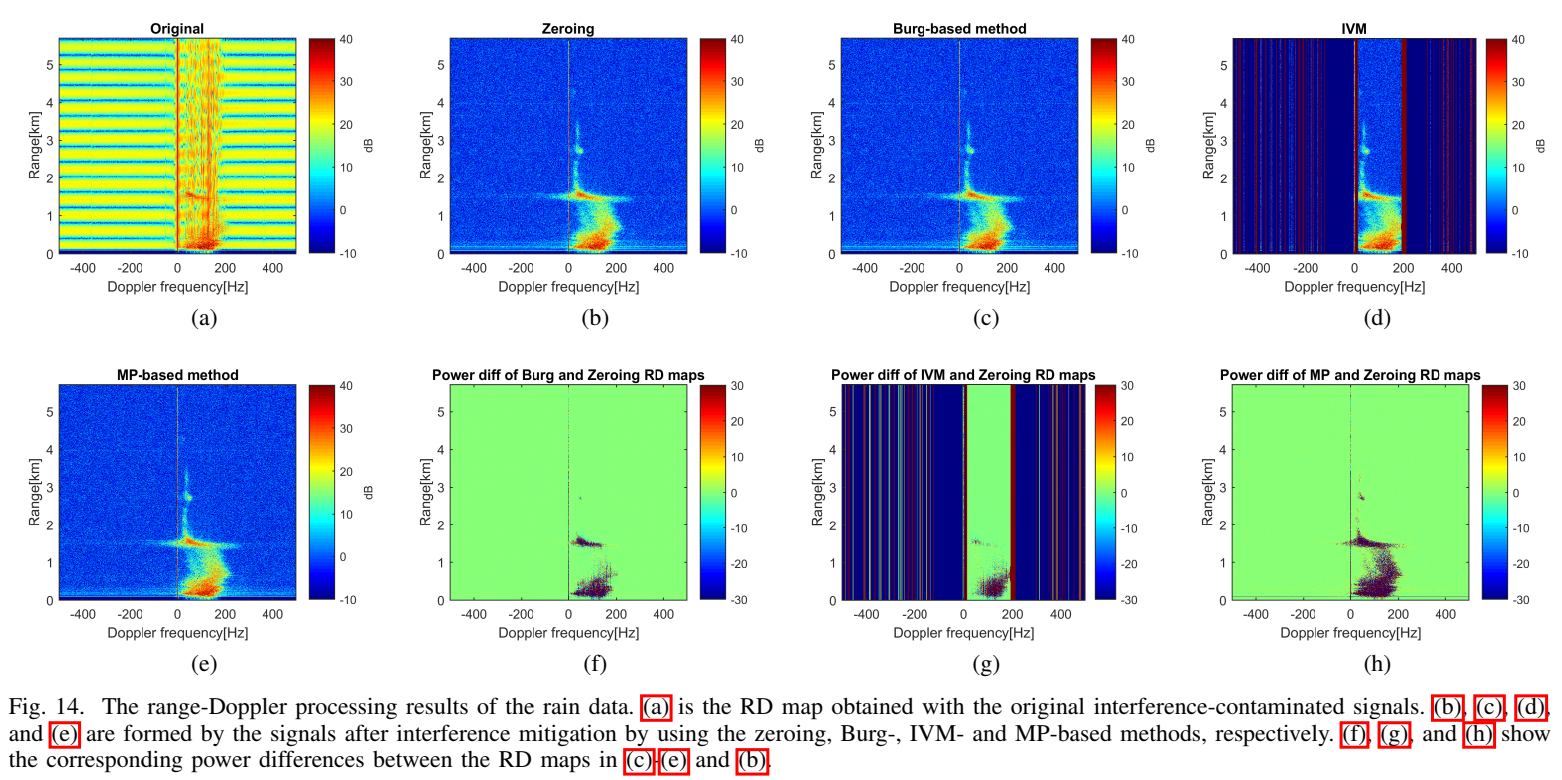
Fig.14(a) 原始 R-D 被干扰覆盖;(b)©(e) 零填/Burg/MP 的 R-D 视觉上都显著改善;(d) IVM 的 blow-up 形成条纹伪迹。由于缺乏 ground truth,作者用"相对零填的功率差分图"(f)(g)(h) 做间接评估:MP 的差分结构更接近实际雨滴 R-D 能量分布,说明其对缺口内信号能量的恢复更可信。
附录 A:从"复指数和"到"全极点/AR"模型的严格等价
作者多次把目标 beat 写为"all-pole model",但正文并没有把"复指数和"与"AR 递推"的桥梁写出来。其实二者是严格等价的:任何有限项复指数和序列都满足一个有限阶的线性递推(即被某个"消去滤波器/annihilating filter"消去)。
设无噪声序列
s[k]=∑i=1M0aizik,zi≠0. s[k]=\sum_{i=1}^{M_0}a_i z_i^k,\quad z_i\neq 0. s[k]=i=1∑M0aizik,zi=0.
构造多项式
A(x)=∏i=1M0(1−zix)=1+c1x+⋯+cM0xM0. A(x)=\prod_{i=1}^{M_0}(1-z_i x)=1+c_1x+\cdots+c_{M_0}x^{M_0}. A(x)=i=1∏M0(1−zix)=1+c1x+⋯+cM0xM0.
注意这里的变量是 xxx,稍后会令 x=q−1x=q^{-1}x=q−1(qqq 为延迟算子)。
因为 A(x)A(x)A(x) 的根是 xi=1/zix_i=1/z_ixi=1/zi,所以对于每个 iii,有
A(1/zi)=0⇒1+c1zi−1+c2zi−2+⋯+cM0zi−M0=0. A(1/z_i)=0\quad\Rightarrow\quad 1+c_1 z_i^{-1}+c_2 z_i^{-2}+\cdots+c_{M_0}z_i^{-M_0}=0. A(1/zi)=0⇒1+c1zi−1+c2zi−2+⋯+cM0zi−M0=0.
两边乘以 zikz_i^{k}zik(对任意 k≥M0k\ge M_0k≥M0 都成立)得
zik+c1zik−1+c2zik−2+⋯+cM0zik−M0=0. z_i^{k}+c_1 z_i^{k-1}+c_2 z_i^{k-2}+\cdots+c_{M_0}z_i^{k-M_0}=0. zik+c1zik−1+c2zik−2+⋯+cM0zik−M0=0.
乘以 aia_iai 并对 iii 求和:
∑i=1M0aizik+c1∑i=1M0aizik−1+⋯+cM0∑i=1M0aizik−M0=0. \sum_{i=1}^{M_0}a_i z_i^{k}+c_1\sum_{i=1}^{M_0}a_i z_i^{k-1}+\cdots+c_{M_0}\sum_{i=1}^{M_0}a_i z_i^{k-M_0}=0. i=1∑M0aizik+c1i=1∑M0aizik−1+⋯+cM0i=1∑M0aizik−M0=0.
由于 ∑iaizik=s[k]\sum_{i}a_i z_i^{k}=s[k]∑iaizik=s[k],得到递推关系
s[k]+c1s[k−1]+c2s[k−2]+⋯+cM0s[k−M0]=0,k≥M0. s[k]+c_1 s[k-1]+c_2 s[k-2]+\cdots+c_{M_0}s[k-M_0]=0,\quad k\ge M_0. s[k]+c1s[k−1]+c2s[k−2]+⋯+cM0s[k−M0]=0,k≥M0.
这就是一个 M0M_0M0 阶 AR(全极点)模型。写成系统函数就是
S(q)⋅(1+c1q−1+⋯+cM0q−M0)=0 S(q)\cdot(1+c_1 q^{-1}+\cdots+c_{M_0}q^{-M_0})=0 S(q)⋅(1+c1q−1+⋯+cM0q−M0)=0
(在"消去滤波器"意义下),或说序列被滤波器
h=[1,c1,...,cM0] h=[1,c_1,\dots,c_{M_0}] h=[1,c1,...,cM0]
消去。这解释了为什么 Burg/IVM 这类 AR 外推能做缺口重建:它们在估计 cmc_mcm;而 MP 是直接估计根 ziz_izi(极点),再回到系数 aia_iai。两条路线在数学上同源,但数值特性不同:根估计往往对噪声更敏感,却能更直接利用 Hankel 低秩结构;系数估计在根密集时可能更稳,但缺口很长时前向/后向分开外推误差会快速累积。
附录 B:为什么 Hankel 矩阵"低秩",以及矩阵铅笔为何能把 ziz_izi 变成广义特征值
这一节补全"MP 的核心定理",也就是从 (15) 一路走到 (22) 背后的数学原因。
B.1 Hankel 因式分解:复指数和 ⇒ Hankel 低秩
对连续序列 s[k]=∑i=1M0aiziks[k]=\sum_{i=1}^{M_0}a_i z_i^ks[k]=∑i=1M0aizik,构造一个 Hankel 矩阵
H0=[s[0]s[1]⋯s[L−1]s[1]s[2]⋯s[L]⋮⋮⋮s[M−L−1]s[M−L]⋯s[M−2]]. H_0= \begin{bmatrix} s[0] & s[1] & \cdots & s[L-1]\\ s[1] & s[2] & \cdots & s[L]\\ \vdots & \vdots & & \vdots\\ s[M-L-1] & s[M-L] & \cdots & s[M-2] \end{bmatrix}. H0= s[0]s[1]⋮s[M−L−1]s[1]s[2]⋮s[M−L]⋯⋯⋯s[L−1]s[L]⋮s[M−2] .
其第 (p,q)(p,q)(p,q) 元素是 H0(p,q)=s[p+q]H_0(p,q)=s[p+q]H0(p,q)=s[p+q]。代入指数和:
H0(p,q)=∑i=1M0aizip+q=∑i=1M0(zip)ai(ziq). H_0(p,q)=\sum_{i=1}^{M_0}a_i z_i^{p+q} =\sum_{i=1}^{M_0}\bigl(z_i^{p}\bigr)a_i\bigl(z_i^{q}\bigr). H0(p,q)=i=1∑M0aizip+q=i=1∑M0(zip)ai(ziq).
定义两个 Vandermonde 型矩阵
V=[11⋯1z1z2⋯zM0⋮⋮⋮z1M−L−1z2M−L−1⋯zM0M−L−1],W=[11⋯1z1z2⋯zM0⋮⋮⋮z1L−1z2L−1⋯zM0L−1]. V=\begin{bmatrix} 1 & 1 & \cdots & 1\\ z_1 & z_2 & \cdots & z_{M_0}\\ \vdots & \vdots & & \vdots\\ z_1^{M-L-1} & z_2^{M-L-1} & \cdots & z_{M_0}^{M-L-1} \end{bmatrix},\quad W=\begin{bmatrix} 1 & 1 & \cdots & 1\\ z_1 & z_2 & \cdots & z_{M_0}\\ \vdots & \vdots & & \vdots\\ z_1^{L-1} & z_2^{L-1} & \cdots & z_{M_0}^{L-1} \end{bmatrix}. V= 1z1⋮z1M−L−11z2⋮z2M−L−1⋯⋯⋯1zM0⋮zM0M−L−1 ,W= 1z1⋮z1L−11z2⋮z2L−1⋯⋯⋯1zM0⋮zM0L−1 .
再定义对角矩阵 A=diag(a1,...,aM0)A=\mathrm{diag}(a_1,\dots,a_{M_0})A=diag(a1,...,aM0)。那么
H0=VAWT. H_0=V A W^T. H0=VAWT.
因此
rank(H0)≤M0. \mathrm{rank}(H_0)\le M_0. rank(H0)≤M0.
只要 V,WV,WV,W 都满列秩(通常要求 L≥M0L\ge M_0L≥M0 且样本足够),在无噪声时 rank 正好等于 M0M_0M0。这就是"信号子空间"存在的数学基础。
B.2 移位 Hankel 与矩阵铅笔:为什么 ziz_izi 会以特征值形式出现
再构造移位 Hankel
H1(p,q)=s[p+q+1]=∑i=1M0aizip+q+1=∑i=1M0(zip)aizi(ziq). H_1(p,q)=s[p+q+1]=\sum_{i=1}^{M_0}a_i z_i^{p+q+1} =\sum_{i=1}^{M_0}\bigl(z_i^{p}\bigr)a_i z_i\bigl(z_i^{q}\bigr). H1(p,q)=s[p+q+1]=i=1∑M0aizip+q+1=i=1∑M0(zip)aizi(ziq).
令 Z=diag(z1,...,zM0)Z=\mathrm{diag}(z_1,\dots,z_{M_0})Z=diag(z1,...,zM0),则
H1=VAZWT. H_1=V A Z W^T. H1=VAZWT.
于是对任意标量 λ\lambdaλ,有
H1−λH0=VA(Z−λI)WT. H_1-\lambda H_0=V A (Z-\lambda I) W^T. H1−λH0=VA(Z−λI)WT.
当 λ=zi\lambda=z_iλ=zi 时,(Z−λI)(Z-\lambda I)(Z−λI) 的第 iii 个对角元为 0,矩阵秩下降(至少下降 1)。因此 λ=zi\lambda=z_iλ=zi 正是使矩阵铅笔 H1−λH0H_1-\lambda H_0H1−λH0 退秩的值,也就对应"广义特征值"。这就是 MP 的根本原理:通过构造两块相差一位的 Hankel,把指数项的"乘 ziz_izi"移位结构转化为一个 pencil 的特征值问题。
附录 C:两段不连续数据为何仍能共享同一组极点,并支撑堆叠 X0,X1X_0,X_1X0,X1
原始目标序列
s[k]=∑i=1M0aizik. s[k]=\sum_{i=1}^{M_0}a_i z_i^k. s[k]=i=1∑M0aizik.
第一段
s1[k]=s[k]=∑i=1M0aizik,k=0,...,N1−1. s_1[k]=s[k]=\sum_{i=1}^{M_0}a_i z_i^k,\quad k=0,\dots,N_1-1. s1[k]=s[k]=i=1∑M0aizik,k=0,...,N1−1.
第二段(注意它从原始索引 N2+1N_2+1N2+1 开始)
s2[k]=s[k+N2+1]=∑i=1M0aizik+N2+1=∑i=1M0(aiziN2+1)⏟≜a~i zik. s_2[k]=s[k+N_2+1]=\sum_{i=1}^{M_0}a_i z_i^{k+N_2+1} =\sum_{i=1}^{M_0}\underbrace{(a_i z_i^{N_2+1})}_{\triangleq \tilde a_i}\; z_i^{k}. s2[k]=s[k+N2+1]=i=1∑M0aizik+N2+1=i=1∑M0≜a~i (aiziN2+1)zik.
这说明:第二段依然是同一组极点 ziz_izi 的复指数和,只是系数变成 a~i=aiziN2+1\tilde a_i=a_i z_i^{N_2+1}a~i=aiziN2+1 。因此分别对两段构造 Hankel 时,会得到
H10=V1AWT,H20=V2A~WT H_{10}=V_1 A W^T,\qquad H_{20}=V_2 \tilde A W^T H10=V1AWT,H20=V2A~WT
其中 A~=diag(a~i)=AZN2+1\tilde A=\mathrm{diag}(\tilde a_i)=A Z^{N_2+1}A~=diag(a~i)=AZN2+1。极点集合 ZZZ 未变。
当把它们竖向堆叠
X0=[H10H20]=[V1V2]AWT(系数差异吸收到 V2 或 A 中都可以), X_0=\begin{bmatrix}H_{10}\\H_{20}\end{bmatrix} =\begin{bmatrix}V_1\\V_2\end{bmatrix}A W^T\quad(\text{系数差异吸收到 }V_2\text{ 或 }A\text{ 中都可以}), X0=[H10H20]=[V1V2]AWT(系数差异吸收到 V2 或 A 中都可以),
同理
X1=[H11H21]=[V1V2]AZWT. X_1=\begin{bmatrix}H_{11}\\H_{21}\end{bmatrix} =\begin{bmatrix}V_1\\V_2\end{bmatrix}A Z W^T. X1=[H11H21]=[V1V2]AZWT.
于是仍然有
X1−λX0=[V1V2]A(Z−λI)WT, X_1-\lambda X_0=\begin{bmatrix}V_1\\V_2\end{bmatrix}A(Z-\lambda I)W^T, X1−λX0=[V1V2]A(Z−λI)WT,
与附录 B 的退秩逻辑完全一致,所以 λ=zi\lambda=z_iλ=zi 仍是该 pencil 的"特征值"。这就解释了 (17) 的堆叠做法为何正确。
附录 D:式 (22) 的推导:从 X1v=λX0vX_1v=\lambda X_0vX1v=λX0v 到降维特征值矩阵
式 (22)给出
det (Σ0−1U0HU1Σ1V1HV0−λI)=0 \det\!\left(\Sigma^{-1}{0}U_0^HU_1\Sigma{1}V_1^HV_0-\lambda I\right)=0 det(Σ0−1U0HU1Σ1V1HV0−λI)=0
(这里我省略下标 M^0\hat M_0M^0,默认都指截断后的 M^0\hat M_0M^0 维块)。
推导思路是:把广义特征向量 vvv 限制在 X0X_0X0 的右奇异向量张成的信号子空间,并用截断 SVD 近似 X0,X1X_0,X_1X0,X1。
从广义特征值方程开始:
X1v=λX0v. X_1 v=\lambda X_0 v. X1v=λX0v.
用截断 SVD 近似
X0≈U0Σ0V0H,X1≈U1Σ1V1H. X_0\approx U_0\Sigma_0 V_0^H,\qquad X_1\approx U_1\Sigma_1 V_1^H. X0≈U0Σ0V0H,X1≈U1Σ1V1H.
由于我们只关心信号子空间内的解,取
v=V0y v=V_0 y v=V0y
(即 vvv 在 V0V_0V0 的列空间内)。代入上式:
U1Σ1V1HV0y=λU0Σ0V0HV0y. U_1\Sigma_1 V_1^H V_0 y=\lambda U_0\Sigma_0 V_0^H V_0 y. U1Σ1V1HV0y=λU0Σ0V0HV0y.
因为 V0HV0=IV_0^H V_0=IV0HV0=I,右侧化简为
λU0Σ0y. \lambda U_0\Sigma_0 y. λU0Σ0y.
于是
U1Σ1V1HV0y=λU0Σ0y. U_1\Sigma_1 V_1^H V_0 y=\lambda U_0\Sigma_0 y. U1Σ1V1HV0y=λU0Σ0y.
左乘 U0HU_0^HU0H:
U0HU1Σ1V1HV0y=λΣ0y. U_0^H U_1\Sigma_1 V_1^H V_0 y=\lambda \Sigma_0 y. U0HU1Σ1V1HV0y=λΣ0y.
再左乘 Σ0−1\Sigma_0^{-1}Σ0−1:
Σ0−1U0HU1Σ1V1HV0y=λy. \Sigma_0^{-1}U_0^H U_1\Sigma_1 V_1^H V_0 y=\lambda y. Σ0−1U0HU1Σ1V1HV0y=λy.
这就是一个普通特征值问题
My=λy,M=Σ0−1U0HU1Σ1V1HV0. My=\lambda y,\quad M=\Sigma_0^{-1}U_0^H U_1\Sigma_1 V_1^H V_0. My=λy,M=Σ0−1U0HU1Σ1V1HV0.
因此
det(M−λI)=0 \det(M-\lambda I)=0 det(M−λI)=0
就是 (22)。其特征值 λi\lambda_iλi 即估计极点 z^i\hat z_iz^i。
这段推导的关键在于两点:第一,用 v=V0yv=V_0 yv=V0y 把未知向量限制到信号子空间;第二,把 X1X_1X1 也投影到与 X0X_0X0 相容的子空间上,从而得到稳定的 M^0\hat M_0M^0 维矩阵。它解释了为什么 MP 需要 SVD,并且为什么截断能抑噪。
附录 E:为什么"零填会导致旁瓣升高/能量损失",用一个频域卷积关系写清楚
作者用图像展示零填的代价,但没有写出频域关系。这里补一个非常直接的表达。
令原始无干扰序列为 s[k]s[k]s[k],零填相当于乘以一个"缺口窗口" g[k]g[k]g[k]:
x[k]=g[k] s[k],g[k]={1,k∉[N1,N2]0,k∈[N1,N2]. x[k]=g[k]\,s[k],\qquad g[k]= \begin{cases} 1,& k\notin[N_1,N_2]\\ 0,& k\in[N_1,N_2]. \end{cases} x[k]=g[k]s[k],g[k]={1,0,k∈/[N1,N2]k∈[N1,N2].
对 x[k]x[k]x[k] 做 NNN 点 DFT 得
X[ω]=∑k=0N−1x[k]e−jωk=∑k=0N−1g[k]s[k]e−jωk. X[\omega]=\sum_{k=0}^{N-1}x[k]e^{-j\omega k} =\sum_{k=0}^{N-1}g[k]s[k]e^{-j\omega k}. X[ω]=k=0∑N−1x[k]e−jωk=k=0∑N−1g[k]s[k]e−jωk.
把 g[k]g[k]g[k] 看作对时域的乘法,则频域是卷积:
X(ω)=12π (G∗S)(ω). X(\omega)=\frac{1}{2\pi}\,(G * S)(\omega). X(ω)=2π1(G∗S)(ω).
而缺口窗口 g[k]g[k]g[k] 可以写成"全 1 窗"减去"矩形缺口窗",其频谱会带有明显的 sinc\mathrm{sinc}sinc 类旁瓣;因此卷积会把原本比较集中的谱峰 S(ω)S(\omega)S(ω) 进行扩散与畸变,表现为距离像旁瓣抬高与主瓣能量泄漏。缺口越长,g[k]g[k]g[k] 的频谱主瓣越窄、旁瓣结构越复杂,卷积造成的畸变越严重。这就是为什么"只零填"在缺口很长时会显著恶化距离像,而重建方法的目标就是尽量让 x[k]≈s[k]x[k]\approx s[k]x[k]≈s[k],等价于让 GGG 的影响消失。
附录 F:低通限定下"干扰出现时刻"的显式解
由式 (11)
fb,I(t)=K1t+K2. f_{b,I}(t)=K_1 t+K_2. fb,I(t)=K1t+K2.
通过低通条件
−fLP≤K1t+K2≤fLP. -f_{\text{LP}}\le K_1 t+K_2\le f_{\text{LP}}. −fLP≤K1t+K2≤fLP.
当 K1>0K_1>0K1>0:
t∈[−fLP−K2K1, fLP−K2K1]. t\in\left[\frac{-f_{\text{LP}}-K_2}{K_1},\;\frac{f_{\text{LP}}-K_2}{K_1}\right]. t∈[K1−fLP−K2,K1fLP−K2].
当 K1<0K_1<0K1<0,不等号方向翻转,但最终可以统一写成
t∈[min (−fLP−K2K1,fLP−K2K1), max (−fLP−K2K1,fLP−K2K1)]. t\in\left[\min\!\left(\frac{-f_{\text{LP}}-K_2}{K_1},\frac{f_{\text{LP}}-K_2}{K_1}\right),\; \max\!\left(\frac{-f_{\text{LP}}-K_2}{K_1},\frac{f_{\text{LP}}-K_2}{K_1}\right)\right]. t∈[min(K1−fLP−K2,K1fLP−K2),max(K1−fLP−K2,K1fLP−K2)].
再与 sweep 的采样窗口 [0,T][0,T][0,T] 求交集,就是实际在 ADC 输出上观察到的污染时间段。它的长度若完全落在窗口内,就是
Δtint=2fLP∣K1∣. \Delta t_{\text{int}}=\frac{2f_{\text{LP}}}{|K_1|}. Δtint=∣K1∣2fLP.
当 K1→0K_1\to 0K1→0 时(斜率极接近),该长度发散,这对应原文所说"极端情况下全段污染,方法失效"。
结束语
把全文总结为一句话:作者把"干扰切割后的缺口"从一个简单插值问题,提升为一个受物理模型约束的参数估计问题;用 MP 在不连续数据上稳健估计指数极点,再通过迭代融合把模型误差压回缺口内部,从而在长缺口、低 SNR 时仍能保持良好重建质量。它的"数学骨架"就是:复指数和 ⇒ Hankel 低秩 ⇒ 铅笔退秩/特征值 ⇒ 极点与系数 ⇒ 缺口重建 ⇒ 迭代融合提升一致性。