【实战】把轨道“掰弯”：用径向推力旋转拱线 (例题 6.8)

【实战】把轨道"掰弯"：用径向推力旋转拱线 (例题 6.8)

💡 摘要：在前面的例子中，我们见识了如何改变轨道的大小。但如果你想改变轨道的"朝向"（即旋转拱线），该怎么办？本文将通过 Curtis 例题 6.8，展示一种简单粗暴的方法：在近地点狠狠地"向外"推一把。这不仅会让轨道变大，还会让它发生显著的旋转。

📚 1. 预备知识 (Prerequisites)

在开始之前，你需要了解：

拱线 (Apseline)：连接近地点和远地点的长轴。
偏心率矢量 (e\mathbf{e}e) ：一个从地心指向近地点的矢量，其大小等于偏心率 eee。
径向推力 (Radial Thrust)：沿着地心连线方向施加的力。通常用来改变轨道的形状或朝向，而不是能量。

🚀 2. 任务背景 (The Mission)

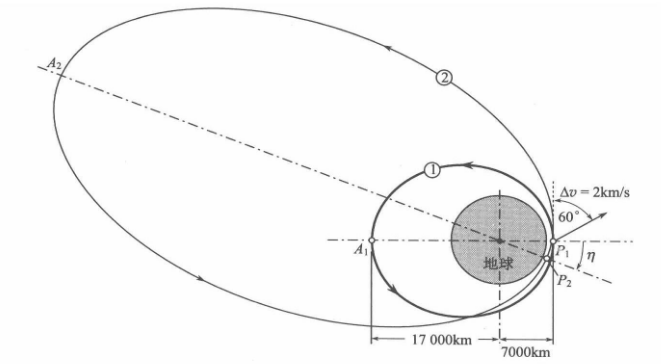
我们的卫星正运行在一条 7000∼17000 km7000 \sim 17000 \text{ km}7000∼17000 km 的轨道上。当它飞到近地点（距离地面最近，速度最快）时，我们决定搞点事情。

任务要求：施加一个 2 km/s2 \text{ km/s}2 km/s 的速度脉冲，方向与原速度方向（水平方向）成 60∘60^\circ60∘ 角，向外指。

输入：轨道参数及脉冲矢量。
目标：计算这一脚下去，轨道的拱线转了多少度 (η\etaη)？
难点：速度矢量的合成改变了运动状态，我们需要重新计算新的偏心率矢量。

🔮 3. 核心魔法：算法解读 (Algorithm Explanation)

本问题的核心在于偏心率矢量的旋转。

3.1 通俗解读

原来的轨道就像一个指向正东方的椭圆。在近地点，卫星本来应该水平飞过。现在我们给它加了一个向外的速度分量，卫星被迫"往上飘"。为了适应这个新的运动轨迹，整个椭圆必须"顺时针"转动，把新的近地点藏到后面去。

3.2 流程图解

输入轨道参数
计算近地点速度 v1
矢量合成: v2 = v1 + Delta v
计算新偏心率矢量 e2
计算旋转角 eta = angle（e2, e1）
输出结果

3.3 关键公式

v2=v1+Δv \mathbf{v}_2 = \mathbf{v}_1 + \Delta \mathbf{v} v2=v1+Δv
解读：最基本的矢量加法。

e=1μ[(v2−μr)r−(r⋅v)v] \mathbf{e} = \frac{1}{\mu} \left[ (v^2 - \frac{\mu}{r}) \mathbf{r} - (\mathbf{r} \cdot \mathbf{v}) \mathbf{v} \right] e=μ1[(v2−rμ)r−(r⋅v)v]
解读：这是轨道力学中的"万能公式"。只要知道位置 r\mathbf{r}r 和速度 v\mathbf{v}v，就能算出轨道的形状 e\mathbf{e}e。通过比较 e2\mathbf{e}_2e2 和 e1\mathbf{e}_1e1 的方向，就能知道轨道转了多少度。

💻 4. Python 代码实战 (Code Deep Dive)

4.1 关键片段一：速度合成

python 复制代码

dvr = delta_v * math.sin(alpha)
dvt = delta_v * math.cos(alpha)
vr2 = 0 + dvr
vt2 = vp1 + dvt

解读：将 2 km/s2 \text{ km/s}2 km/s 的脉冲分解为径向（向外）和横向（向前）两个分量，叠加到原速度上。

4.2 关键片段二：偏心率矢量计算

python 复制代码

r_vec = [rp1, 0, 0]
v_vec = [vr2, vt2, 0]
# ... 代入万能公式 ...
eta = math.degrees(math.atan2(ey, ex))

解读：直接利用 Python 的向量运算能力，算出新的 e\mathbf{e}e 矢量分量。atan2 函数会告诉我们它相对于原轴线转了多少度。

4.3 关键片段三：结果输出

python 复制代码

print(f"Orbit 2: e2={e2:.5f}")
print(f"Rotation Angle eta: {eta:.2f} deg")

解读：输出最终的旋转角度。

4.4 求解技巧 (Pro Tips)

技巧 1 ：在近地点建立坐标系是最方便的。此时 r\mathbf{r}r 只有 xxx 分量，v1\mathbf{v}_1v1 只有 yyy 分量。
技巧 2 ：η\etaη 的符号很重要。负值表示顺时针旋转，正值表示逆时针。

4.5 避坑指南 (Pitfalls)

⚠️ 高能预警：

能量巨变：虽然我们的目标是旋转拱线，但这次机动同时也极大地改变了偏心率（从 0.4 变到了 0.8）。如果只想旋转而不改形状，需要更复杂的双脉冲策略。

撞地风险 ：新的偏心率高达 0.8，需要检查近地点高度是否低于地球半径（RE≈6378R_E \approx 6378RE≈6378 km）。在本例中，新轨道近地点可能会非常低！

📊 5. 结果揭秘 (The Result)

5.1 中间过程验证

text 复制代码

Orbit 1: e1=0.41667
Velocity at P1: 8.9816 km/s
Maneuver: dvr=1.7321, dvt=1.0000

分析：我们在 9 km/s 的水平速度上，硬生生加了 1.7 km/s 的垂直速度。

5.2 最终结果

text 复制代码

Orbit 2: e2=0.80883
Rotation Angle eta: -22.05 deg

数据分析：

η≈−22∘\eta \approx -22^\circη≈−22∘：轨道顺时针旋转了 22 度。
e2≈0.81e_2 \approx 0.81e2≈0.81：轨道变得极扁。如果不加控制，这颗卫星可能在绕回来时直接再入大气层。

🧠 6. 扩展思考：其他解法 (Alternative Approaches)

方法一：几何法
- 原理：利用真近点角公式 tan⁡θ=pvrhe\tan \theta = \frac{p v_r}{h e}tanθ=hepvr。在机动点，我们知道 r,v,ϕr, v, \phir,v,ϕ，可以直接算出该点在新轨道上的真近点角 θ2\theta_2θ2。由于机动点在原轨道是 θ1=0\theta_1=0θ1=0，所以旋转角 η=0−θ2=−θ2\eta = 0 - \theta_2 = -\theta_2η=0−θ2=−θ2。
- 优缺点：计算更快捷，不需要构造矢量，但物理图像不如矢量法直观。

🌌 7. 工程应用与展望 (Engineering Impact)

应用场景 ：这种利用径向推力的机动常用于轨道维持，微调近地点或远地点的位置。
局限性：效率较低。改变平面内形状通常在切向施加推力更省燃料。径向推力主要用于改变方位的"微操"。

📝 8. 总结 (Summary)

通过本例，我们掌握了：

偏心率矢量法：处理轨道旋转问题的终极武器。
径向推力的作用：它能有效旋转拱线，但也会显著改变轨道形状。
坐标系的选择：在特征点（如近地点）建立坐标系能大大简化计算。

声明

本文由AI生成，经人工审核，过程和结果均符合预期。