6.1间隔与支持向量
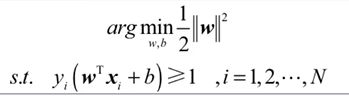
训练的过程如上图,支持向量机找到最大化分类间隔的最优化线性函数,该线性函数称为超平面,此时它的鲁棒性最好,也具有很好的泛化性能。s.t.表示满足,受限于,所以整体表示为满足下式情况下,求上式的最小值。

求解出支持向量机需要解决这三个主要问题,后续内容围绕此发展。
6.2对偶问题

解决问题一,注意支持向量机是函数值>=1。


图分别展示了用拉格朗常数法求解的过程,但因为用到不等式,这里其实牵扯到KKT条件,进而推出支持向量机其实主要是由在距离间隔两条线上的样本决定,即αi不成立,第二个条件成立时的情况。简化运算为关于α相关函数就是对偶问题。
SMO计算:

为求解对偶问题的式子,用SOM算出αi和αj,最后能算得使对偶函数最大的α向量,也是支持向量上的向量。

6.3核函数

即寻找最优映射高维特征的函数。
6.4软间隔和正则化
软间隔允许少部分样本不满足约束,采用松弛变量和(对应样本违反间隔约束的总程度)列出目标函数求解,其中C为罚函数法。
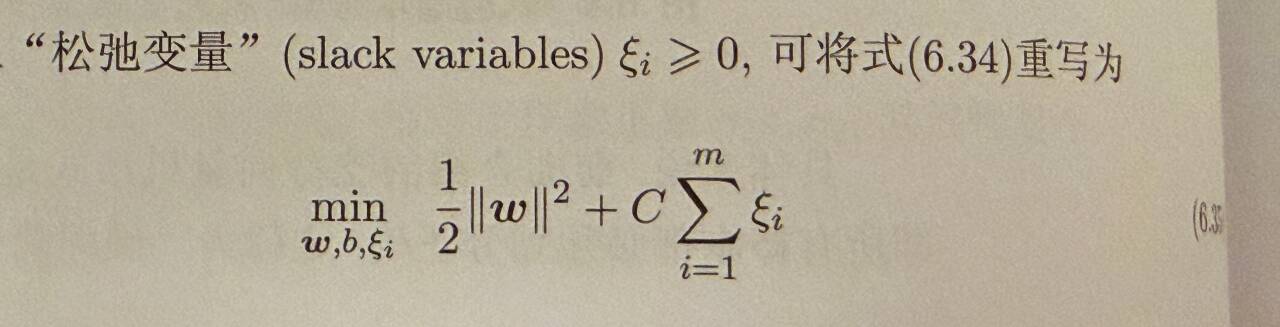
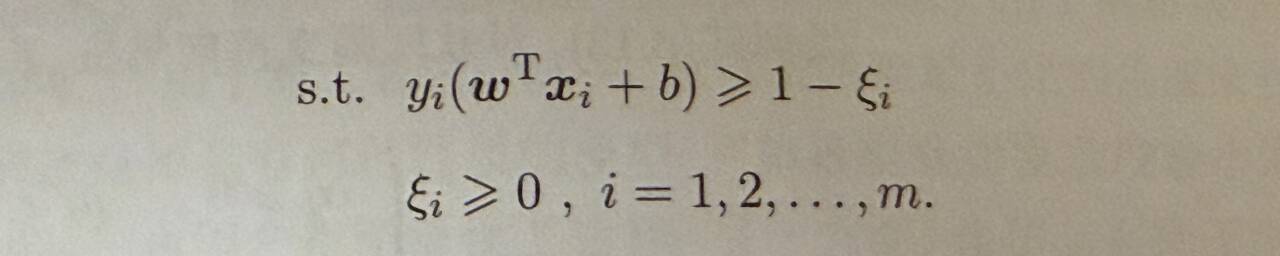
后续还是拉格朗日函数偏导求解带入得到对偶函数,用KKT证明就是软间隔支持向量,最后SMO迭代得到w*和b*,w*代表最优超平面法向量唯一解。
6.5支持向量回归


支持向量回归是回归任务的分支,目标是找到一个宽度为2s的间隔带,让尽可能多的样本落入带内,实现连续值的预测。
6.6核方法
这里讲到了KLDA,相较于前面提到的低维LDA这一个分类问题,是基于核函数进行运算升维,到可分类维度进行映射运算的。