【实战】共拱线的“漂移”：如何优雅地给卫星来一脚？ (例题 6.6)

【实战】共拱线的"漂移"：如何优雅地给卫星来一脚？ (例题 6.6)

💡 摘要：本文将带你围观一场卫星变轨的"暴力美学"。当卫星不想走寻常路（霍曼转移）时，我们如何通过一次精准的脉冲机动，让它在共享拱线的两条椭圆轨道间横跳？我们将深度解析 Curtis 教材中的例题 6.6，用 Python 揭开速度增量 Δv\Delta vΔv 的神秘面纱。

📚 1. 预备知识 (Prerequisites)

在开始这场星际漂移之前，你需要装备以下姿势：

真近点角 (θ\thetaθ) ：卫星在轨道上的"进度条"，从近地点开始算起，跑一圈是 360∘360^\circ360∘。
飞行路径角 (ϕ\phiϕ) ：速度矢量与当地地平线的夹角。如果 ϕ>0\phi > 0ϕ>0，说明卫星正在"爬坡"（远离地心）。
共拱线 (Common Apseline)：两条轨道的"长轴"重合。就像是两张椭圆形的饼，虽然大小不一，但中心和中轴线是对齐的。

🚀 2. 任务背景 (The Mission)

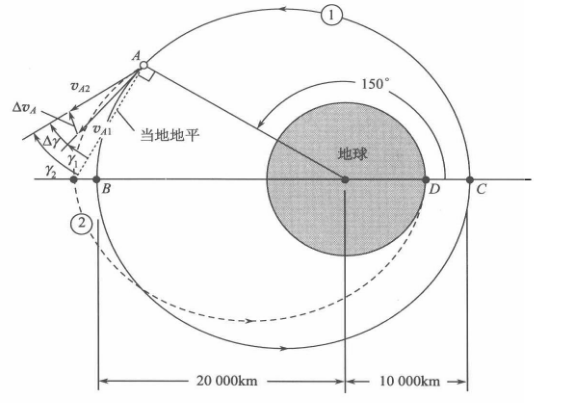
想象你是一名航天指挥官，你的卫星正悠闲地在轨道 1 上晃悠。突然，上级要求卫星执行一次机动，去"亲吻"地球表面（到达 D 点，即近地点高度降至地球半径）。

最关键的是，这次机动必须在 A 点（真近点角 150∘150^\circ150∘）完成。这就像是在高速公路上，不仅要换道，还得在指定的出口前完成一次"神龙摆尾"。

输入：轨道 1 的近/远地点半径，机动点 A 的位置，轨道 2 的目标近地点。
目标：计算这一脚油门（Δv\Delta vΔv）该怎么踩，往哪儿踩。
难点：这不是简单的加减速，而是速度矢量的重新合成。

🔮 3. 核心魔法：算法解读 (Algorithm Explanation)

本问题的核心在于共拱线轨道切换算法。

3.1 通俗解读

这本质上是一场速度矢量的"外科手术" 。卫星在 A 点原本有一个速度 v1\mathbf{v}_1v1，我们给它补上一个脉冲 Δv\Delta \mathbf{v}Δv，使其瞬间变成轨道 2 所需的速度 v2\mathbf{v}_2v2。由于位置没变，只有速度变了，这就是所谓的"脉冲假设"。这就像是在冰面上滑行时，被另一股侧向力量猛推了一把，瞬间改变了航向和快慢。

3.2 流程图解

输入轨道1参数与机动点A
计算A点在轨道1的速度分量
根据目标近地点计算轨道2偏心率
计算A点在轨道2的速度分量
矢量合成: Delta v = v2 - v1
输出速度增量大小与方向

3.3 关键公式

r=h2/μ1+ecos⁡θ r = \frac{h^2/\mu}{1 + e \cos \theta} r=1+ecosθh2/μ
解读：轨道方程是我们的"地图"，它定义了卫星在特定真近点角处的径向距离。

vr=μhesin⁡θ,vθ=hr v_r = \frac{\mu}{h} e \sin \theta, \quad v_{\theta} = \frac{h}{r} vr=hμesinθ,vθ=rh
解读：速度分解公式。将速度拆解为径向（上下）和横向（左右），这是矢量合成的前提。

e2=rA−rp2rp2−rAcos⁡θA2 e_2 = \frac{r_A - r_{p2}}{r_{p2} - r_A \cos \theta_{A2}} e2=rp2−rAcosθA2rA−rp2
解读：偏心率反求公式。这是变轨的关键，决定了轨道 2 的"体型"。

Δv=(vr2−vr1)2+(vθ2−vθ1)2 \Delta v = \sqrt{(v_{r2} - v_{r1})^2 + (v_{\theta 2} - v_{\theta 1})^2} Δv=(vr2−vr1)2+(vθ2−vθ1)2
解读：最终的暴力美学，通过分量差的平方和根号得到总的速度增量。

💻 4. Python 代码实战 (Code Deep Dive)

我们如何用 Python 实现它？我们将核心逻辑拆解为三个关键部分。

4.1 关键片段一：解析轨道 1 与机动点

python 复制代码

e1 = (ra1 - rp1) / (ra1 + rp1)
h1 = math.sqrt(mu * rp1 * (1 + e1))
r_a = (h1**2 / mu) / (1 + e1 * math.cos(theta_a1))

解读：这段代码先算出了轨道 1 的"身材"（偏心率）和"能量"（角动量），并确定了机动发生时的精确位置 rAr_ArA。

4.2 关键片段二：轨道 2 的"整容"逻辑

python 复制代码

e2 = (rp2 - r_a) / (r_a * math.cos(theta_a2) - rp2)
h2 = math.sqrt(mu * rp2 * (1 + e2))

解读：根据目标近地点高度，逆推轨道 2 的参数。这就像是根据你想去的终点，倒推这脚油门该怎么踩。

4.3 关键片段三：速度矢量的"乾坤大挪移"

python 复制代码

dvr = vr2 - vr1
dvt = vt2 - vt1
dv = math.sqrt(dvr**2 + dvt**2)
beta = math.degrees(math.atan2(dvr, dvt))

解读：计算两个轨道在 A 点的速度差，并使用 atan2 优雅地处理方向角，避免象限混乱。

4.4 求解技巧 (Pro Tips)

技巧 1 ：利用 math.atan2(y, x) 而不是 atan(y/x)，这在处理全圆角度（0∘0^\circ0∘ 到 360∘360^\circ360∘）时能自动识别正负号和象限。
技巧 2 ：在计算 e2e_2e2 时，注意共拱线前提下的 θA2\theta_{A2}θA2 依然是 150∘150^\circ150∘，因为两条轨道的近地点方向是一致的。

4.5 避坑指南 (Pitfalls)

⚠️ 高能预警：

弧度制陷阱 ：math.sin 和 math.cos 接收的是弧度，记得用 math.radians() 转换。

单位统一 ：确保 μ\muμ 的单位（km3/s2\text{km}^3/\text{s}^2km3/s2）与 rrr 的单位（km）一致，否则结果会差出几个量级。

物理方向 ：β\betaβ 角是从当地地平线逆时针测量的，如果结果大于 90∘90^\circ90∘，说明有"刹车"分量。

📊 5. 结果揭秘 (The Result)

运行脚本 solve_6_6.py，让我们看看程序输出了什么。

5.1 中间过程验证

在得出最终结果前，我们先检查中间变量是否合理：

text 复制代码

[Step 1] 轨道 1 偏心率 e1 = 0.333333
[Step 2] 机动点半径 rA = 18744.37 km

text 复制代码

[Step 3] 轨道 2 偏心率 e2 = 0.546916
[Step 4] 轨道 2 角动量 h2 = 62711.07 km^2/s

分析：这里的结果表明卫星从一个相对圆润的轨道切换到了一个非常扁平的轨道，以实现近地点高度的剧降。

5.2 最终结果

text 复制代码

Total Delta V (dv): 0.989584 km/s
Direction beta (rel. to horizon): 123.33 deg

数据分析：

这一脚有多狠？ 接近 1 km/s 的速度增量。在航天领域，这绝对是大手笔，得烧不少燃料。
方向在哪？ 123.33∘123.33^\circ123.33∘。这意味着你不仅要往"后"踩刹车（横向分量为负），还得往"外"推一把（径向分量为正）。

🧠 6. 扩展思考：其他解法 (Alternative Approaches)

除了本文介绍的解析法，还有哪些路可以通罗马？

方法一：数值积分法
- 原理：直接建立二体受力方程，在 A 点施加一个猜测的脉冲，看卫星轨迹是否经过 D 点。
- 优缺点：精度极高，能考虑非球形引力，但计算量大，且需要复杂的迭代过程。
方法二：兰伯特问题（Lambert's Problem）求解
- 原理：已知起点 A、终点 D 和飞行时间，反求转移轨道。
- 优缺点：更具通用性，但对于共拱线这类特定几何约束的问题，解析法往往更直观。

🌌 7. 工程应用与展望 (Engineering Impact)

这个问题在真实的航天工程中意味着什么？

应用场景 ：这种非霍曼转移常用于紧急重返大气层 或轨道截击任务。当任务对时间或特定几何位置有严格要求，且燃料充足时，这种变轨方式非常有效。
局限性：本模型忽略了地球非球形摄动（J2 项）。在真实任务中，由于 J2 摄动，轨道的拱线会缓慢旋转，维持"共拱线"需要额外的控制。
未来展望：随着电推进技术的发展，连续小推力转移正在取代这种瞬时脉冲机动，但理解脉冲机动的物理本质依然是航天动力学的基础。

📝 8. 总结 (Summary)

通过这个案例，我们掌握了：

轨道方程的逆推技巧：如何根据一个点和轨道特征反求偏心率。
速度矢量的精细分解：径向和横向分量在变轨中的不同作用。
非霍曼转移的代价：深刻理解了非最优路径下换取特定几何约束的燃料成本。
Python 在动力学中的应用 ：如何利用 math 库快速验证复杂的轨道几何问题。

声明

本文由AI生成，经人工审核，过程和结果均符合预期。