充分利用未来已知信息：DAG 用双因果结构把 TSF-X 时序预测推到新高度

充分利用未来已知信息：DAG 用双因果结构把 TSF-X 时序预测推到新高度

B站懒羊羊吃辣条-2026-01-21
论文名称：DAG: A Dual Causal Network for Time Series Forecasting with Exogenous Variables

论文引用：Qiu X, Zhu Y, Li Z, et al. Dag: A dual causal network for time series forecasting with exogenous variables[J]. arXiv preprint arXiv:2509.14933, 2025.

论文链接：https://arxiv.org/abs/2509.14933

一、这篇论文在做什么

DAG 研究的是"当你做时间序列预测时，除了目标序列的历史数据，还拥有一堆外生协变量（其中一部分在未来也能提前知道）时，如何更稳健、更有效地用这些外生信息"，并用"可迁移的因果结构"去约束模型的融合方式，从而提升预测精度与泛化稳定性。

你要预测一个数值（销量、客流、流量、价格、传感器读数、设备状态......），通常你会同时拥有：

• 目标序列的历史（内生变量）：比如过去 7 天的销量。
• 外部协变量的历史（外生变量）：比如过去的促销标记、天气、节假日、宏观指标、上游系统输出等。
• 外部协变量的未来（未来外生变量）：比如未来的日历是确定的、促销计划是已排期的、天气预报是可查询的、策略/控制量是已规划的，或未来某些上游预测结果可以提前拿到。

论文讨论的任务设定（TSF-X）就是：

输入：历史内生 + 历史外生 + 未来外生；输出：未来内生。

个人感觉这篇工作比较适合光伏发电量预测和电力负荷预测领域。因为它覆盖了很多真实业务：

• 零售/营销：未来促销、节假日是已知的；
• 城市交通/客流：未来日历与事件排期可能已知；
• 工业过程：未来控制量/设定值在计划控制里往往是已知的；
• 气象相关预测：天气预报可得，影响下游序列（需求、出行、能耗等）。

创新点1：不把外生变量当"拼在一起的特征"，而是把它当"可以学习结构的信号源"

很多模型的做法是：把所有变量直接拼接/做注意力，让模型自己决定怎么用未来外生变量。DAG 认为这样容易学到短期有效但不稳定的相关性（换数据集/换时间段就崩）。

创新点2：把"因果"用作一种工程上的"结构约束/归纳偏置"

注意：论文里的"因果"更像"可迁移依赖结构"，而不是要输出一张明确可解释的因果图。它做的是：先在某些"更容易学、信号更强"的关系上学习到依赖结构；再把这种结构注入到最终预测里，让模型融合外生变量时更有章法。

创新点3：同时抓两种"结构相似性"：时间维度 + 变量维度

• 时间维度（temporal）相似性： 外生变量自己也有时间演化规律，"历史外生 → 未来外生"的演化结构，往往和"历史目标 → 未来目标"的演化结构在形式上相似（比如都有趋势、季节性、突变）。
• 变量维度（channel）相似性： 外生变量与目标变量之间的影响关系，"外生 → 目标"的结构在历史与未来之间应当相对一致（比如促销对销量的作用、日历对客流的作用）。

DAG 就是围绕这两种相似性设计了"双模块：时间因果模块 + 通道因果模块"，并用"发现→注入"的方式把结构迁移到最终预测里。

二、为什么要做：痛点与背景

做时间序列预测时，很多人一开始默认的是：

"用目标序列的历史值去预测目标序列的未来值。"

这在很多场景能得到很好的效果，但一旦进入更真实、更复杂的任务，就会遇到三个典型痛点，而这篇论文正是围绕它们展开的。

痛点 1：现实任务里，"外生变量"几乎无处不在，而且其中一部分在未来是可知的

在通用时序预测里，除了目标序列本身，通常还会有大量外部协变量（论文称 exogenous variables/covariates）。比如：

• 日历类：星期几、是否节假日、季节等（未来往往是确定的）；
• 计划/策略类：促销排期、价格策略、生产计划、控制设定值（未来往往是确定的）；
• 环境类：天气预报、宏观指标预告、事件排期（未来往往可获取但有误差）；
• 上游系统输出：上游预测结果或传感器先验（未来可能可用）。

因此，论文强调的 TSF-X 设定非常关键：预测时不只给你历史外生变量，还给你未来外生变量 (Y_{exo})。这类设定如果利用得当，预测上限会明显更高。

痛点 2：很多方法要么"不用未来外生变量"，要么"用得很粗糙"，导致信息浪费或泛化不稳

论文在引言里把方法大致分为四类，并指出现有路线的局限：

• 不考虑外生变量（a图）：只建模目标序列自身动态，遇到强外部驱动时容易吃亏；
• 只用历史外生变量（b图）：把外生当作过去的辅助特征，但对"未来已知信息"无能为力；
• 同时用历史与未来外生变量（c图）：信息更全，但很多做法是直接拼接或注意力融合，缺少结构约束；
• DAG（d图）：不仅使用未来外生变量，还显式利用因果结构（更准确说是"可迁移依赖结构"）来指导融合。

这里有一个工程上很关键、但常被忽视的问题：

外生变量一多，相关性几乎到处都是；模型若没有约束，很容易"抓住错误的相关性"，短期看准确，换一段时间或换一个场景就不稳。

这也是为什么作者强调"仅靠相关性不够"，需要把注意力机制里的依赖学习用更稳定的结构去约束。

痛点 3：时序预测里存在两类"结构相似性"，但过去的方法没把它用起来

• 时间维度的相似性（Similar Temporal Causality）： 外生变量也在随时间演化，"历史外生→未来外生"的依赖结构，与"历史目标→未来目标"的依赖结构往往在形式上相近。直观理解：都可能有趋势、季节性、突变等时间规律。
• 变量维度的相似性（Similar Channel Causality）： 外生与目标之间的作用关系在历史与未来之间应该具有一致性：如果历史上"外生A"对目标有影响，那么未来当外生A变化时，这种影响方向与机制大概率仍然成立。

把这两点合起来，作者的论证逻辑是：

与其直接让模型在"高维外生变量 + 长序列"上盲目学依赖，不如先在更容易的关系上学到可迁移的依赖结构，再把结构注入到最终预测里。

这也解释了 DAG 的名称与思路：它借用"因果（causality）"的视角，不是为了给出可解释因果图，而是为了引入一种更稳健的学习偏置，减少伪相关风险。

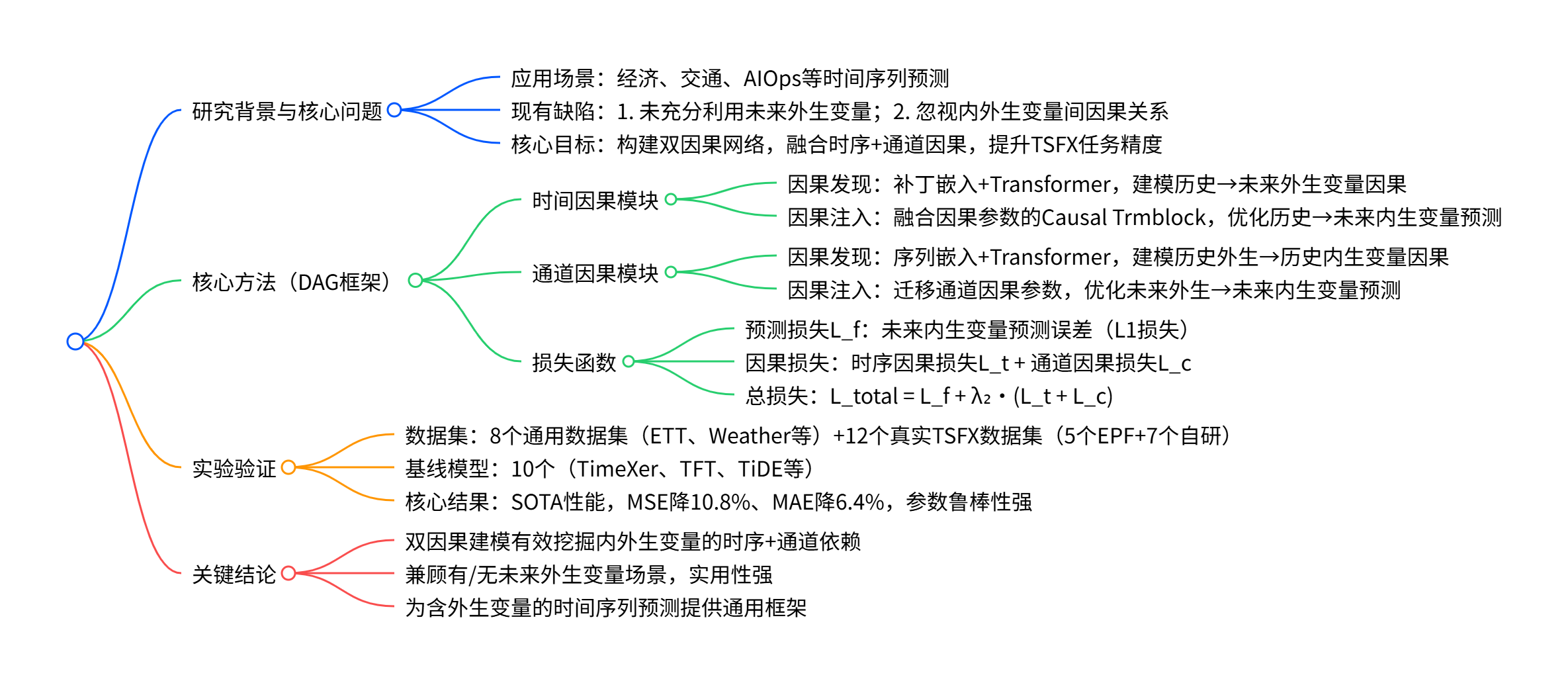
三、怎么做：方法框架拆解

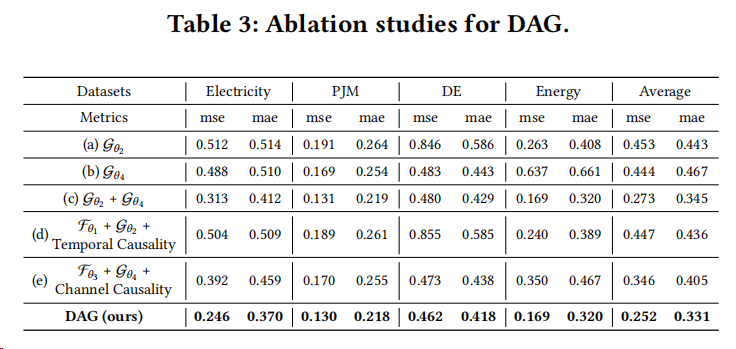
DAG 的核心不是"把外生变量堆进模型"，而是先用外生变量完成两个更容易的辅助任务，学出一套可迁移的依赖结构。 具体做法是两条分支并行：一条沿时间学"外生变量怎么演化"，一条沿变量学"外生变量怎么影响目标"，每条分支都遵循"先发现、再注入"。所谓"注入"，就是把发现阶段学到的注意力投影矩阵 (Wq′,Wk′)(W_q',W_k')(Wq′,Wk′)带进最终预测的注意力计算里，并用门控系数自适应融合"模型自己学的注意力"和"结构引导的注意力"。最后，时间分支和通道分支各给一个预测，再用融合成最终输出，并用 (Lf+λ2(Lt+Lc)(L_f+\lambda_2(L_t+L_c)(Lf+λ2(Lt+Lc) 联合训练，确保"学结构"真的能服务于最终预测。

3.1 先把 TSF-X 这件事说清楚

做预测时，我们手里有三种信息：

• 目标序列的历史（论文叫内生）：过去发生了什么（例如销量/流量/价格的历史）。
• 外生变量的历史：过去的"影响因素"是什么（节假日、促销、天气、策略、上游预测等）。
• 外生变量的未来：未来的"影响因素"你往往也能提前知道一部分（未来日历、促销排期、天气预报、控制设定值等）。

任务就是：

输入（历史目标 + 历史外生 + 未来外生），输出（未来目标）。

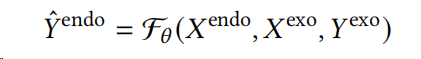
3.2 DAG 的"总体框架"：两条路并行跑，最后合票

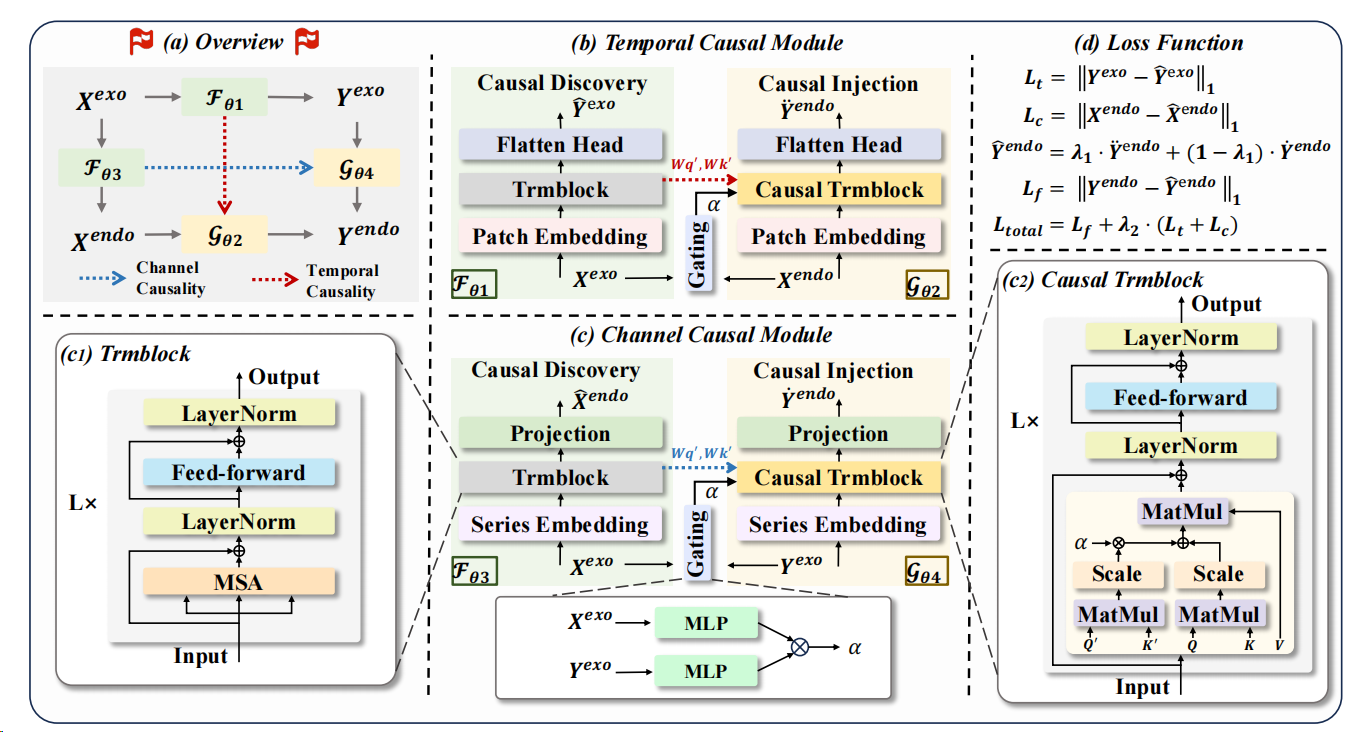
作者把模型分成两条并行分支：

• 时间因果分支（Temporal）：重点解决"沿时间怎么迁移结构"。
• 通道因果分支（Channel）：重点解决"不同变量之间的关系怎么迁移结构"。

两条分支各自产出一个对未来目标的预测，然后用一个权重混合成最终结果。

3.3 每条分支都做两件事：先"学结构"，再"用结构"

DAG 的核心设计是一个非常"工程化"的两步走：

第一步：Causal Discovery（先学结构） 它先做一个相对容易、信号更强的"辅助预测任务"，目的不是为了预测本身，而是为了从中抽出一套稳定依赖结构。

第二步：Causal Injection（再用结构） 把第一步学到的结构注入到真正的"目标预测"里，让模型在用外生变量时更有章法。

最重要的细节在这里： 作者把"结构"具体实现为注意力机制里的两组参数 (W_q',W_k')（Query/Key 的投影矩阵），并把它们注入到最终预测的注意力计算里。

你可以把 (W_q',W_k') 当作"依赖关系的模板"：它告诉模型更倾向于关注哪些模式，而不是完全从零开始乱学。

3.4 时间因果分支：用"外生的时间演化"当老师，教目标怎么沿时间看

这一支分两步：

（1）先学结构：用历史外生去预测未来外生 输入是(Xexo)，目标是预测(Y^exo)，并计算时间因果损失(Lt=∣Yexo−Y^exo∣1),关键不是预测外生本身，而是从这个过程中抽出(Wq′,Wk′)，作为"时间结构模板"。输入是 (X_{exo})，目标是预测 (\hat{Y}{exo})，并计算时间因果损失(L_t=|Y{exo}-\hat{Y}_{exo}|_1),关键不是预测外生本身，而是从这个过程中抽出 (W_q',W_k')，作为"时间结构模板"。 输入是(Xexo)，目标是预测(Y^exo)，并计算时间因果损失(Lt=∣Yexo−Y^exo∣1),关键不是预测外生本身，而是从这个过程中抽出(Wq′,Wk′)，作为"时间结构模板"。

（2）再用结构：预测未来目标时，把这套时间结构注入注意力 当它用历史目标Xendo预测未来目标时，会在注意力里同时计算两套分数一套来自当前分支自己学的(Wq,Wk)一套来自"外生时间老师传下来的"(Wq′,Wk′)然后用一个权重(α)把两套注意力分数融合当它用历史目标X_{endo}预测未来目标时， 会在注意力里同时计算两套分数 一套来自当前分支自己学的(W_q,W_k) 一套来自"外生时间老师传下来的" (W_q',W_k') 然后用一个权重 (\alpha) 把两套注意力分数融合当它用历史目标Xendo预测未来目标时，会在注意力里同时计算两套分数一套来自当前分支自己学的(Wq,Wk)一套来自"外生时间老师传下来的"(Wq′,Wk′)然后用一个权重(α)把两套注意力分数融合

3.5 通道因果分支：用"外生→目标"的历史关系当老师，教未来外生怎么影响未来目标

这一支也分两步，但"老师"换了：它教的是变量之间的影响关系。

（1）先学结构：用历史外生去预测历史目标 输入(Xexo)，输出(X^endo)，并计算通道因果损失(Lc=∣Xendo−X^endo∣1)输入 (X_{exo})，输出 (\hat{X}{endo})，并计算通道因果损失(L_c=|X{endo}-\hat{X}_{endo}|_1) 输入(Xexo)，输出(X^endo)，并计算通道因果损失(Lc=∣Xendo−X^endo∣1)

同样，过程中抽出 (W_q',W_k') 当作"变量关系模板"。

（2）再用结构：用未来外生预测未来目标时，把变量关系注入注意力 当用 (Y_{exo}) 去预测未来目标时，注意力里也会同时看两套分数并融合，(\alpha) 由历史外生与未来外生的编码点积得到。

历史上"哪些外生因素会影响目标"是一堂高质量的课；DAG 让模型把这堂课的笔记带到未来去用，而不是未来再从零猜一遍。

3.6 为什么要用"门控 α + 两条分支融合 λ1"？

这里作者做了两层"保险"：

保险 1：注意力层面用 α 融合 不是强行要求"全听老师的"，也不是"完全自己学"，而是让模型自适应决定：这一次更该相信自身学习的注意力，还是更该相信注入的结构。

保险 2：输出层面用 λ1 融合两条分支 时间分支与通道分支各有擅长场景，最终用 (\lambda_1) 融合。

3.7 训练怎么保证"学结构"不是摆设？三项损失一起约束

DAG 不是只盯着最终预测误差，还把两条"老师任务"也一起训练：

• (L_t)：预测未来外生（时间老师）
• (L_c)：预测历史目标（通道老师）
• (L_f)：最终预测未来目标

总损失是：(Ltotal=Lf+λ2(Lt+Lc))(L_{total}=L_f+\lambda_2(L_t+L_c))(Ltotal=Lf+λ2(Lt+Lc))

你不能只让学生做"最终考试题"（预测未来目标），还要让他把"老师布置的练习题"（两个发现任务）认真做完，才能真正学到可迁移的结构。

四、实验与结果

4.1 作者怎么做实验

（1）两组数据集，两种现实程度 作者把实验分成两大块：

• 8 个常见公开多变量数据集（ETT 四个子集、Weather、Exchange、Electricity、Traffic）：这些数据集严格来说并不天然提供"可知未来外生变量"，作者采用一种 vanilla TSF-X 处理：把多变量序列的最后一维当作预测目标（内生），其余维度当作外生变量来做 TSF-X 设定。
• 12 个满足 TSF-X 条件的真实数据集：这里的未来外生变量被认为"近似可知或高度准确"，更接近真实业务设定。

（2）对比模型覆盖两大阵营：能原生用未来外生 vs 不能 基线一共 10 个，作者特别强调了公平性处理：对那些原本不支持未来外生变量的模型，用一个统一的 MLP fusion 方式把未来外生并入输入（算法在附录 A.3）。 这点很重要，因为它避免了"DAG 用了未来外生、别人没用"的不公平。

（3）评价指标与预测设置

• 指标：MSE、MAE。
• 8 个公开数据集：lookback 固定 96，预测 horizon 取 {96, 192, 336, 720}（表 1 给的是平均效果；全量结果在附录表 6）。
• 12 个真实 TSF-X 数据集：同时做短期与长期两档（如多数数据集用 168→24、720→360；Colbún/Rapel 用 60→10、180→30）。

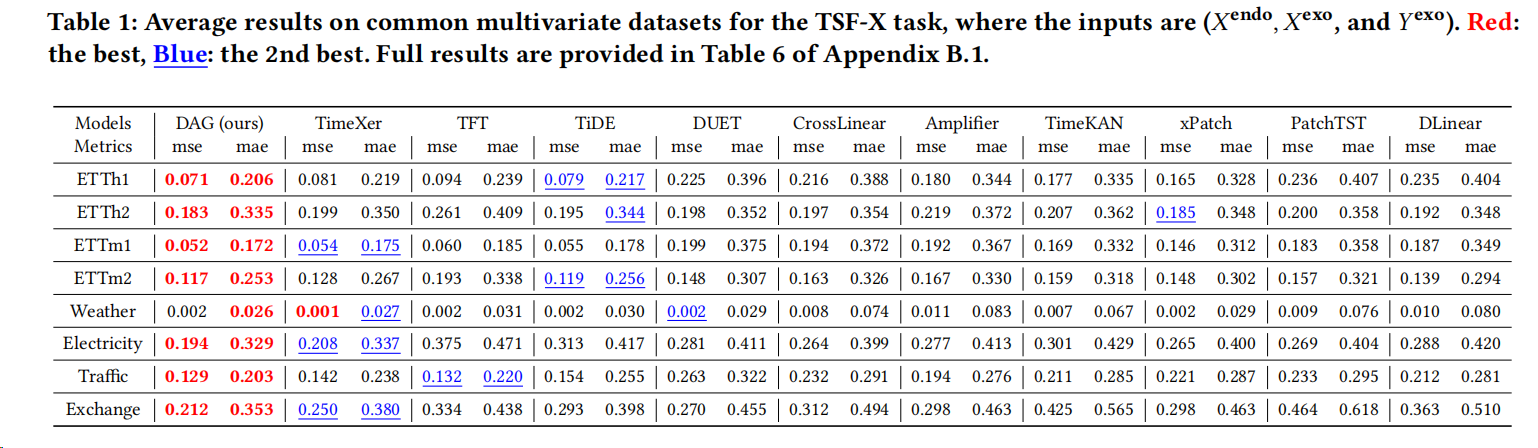
4.2 主要实验结论

作者自己在论文里把主结论总结得很直接：

• 在常见多变量数据集（表 1）上，DAG 相比第二名 TimeXer MSE 下降 10.8%，MAE 下降 6.4%。
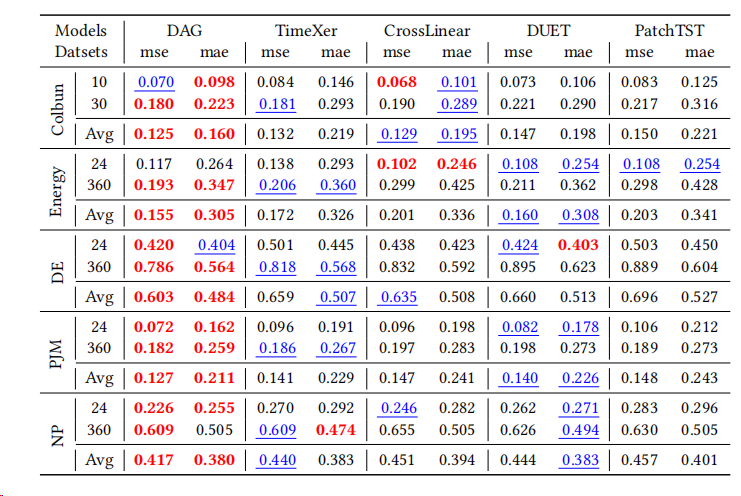
• 在真实 TSF-X 数据集（表 2）上，DAG 拿到的"第一名次数"最多：MSE 26 次第一、MAE 29 次第一。

4.3 它"强"在哪里：不是只强在一个点，而是强在三层逻辑

强点 1：在"未来外生变量确实重要"的设定里，它吃到了真正的增益 作者指出：原生支持未来外生的模型（TiDE、TFT、TimeXer）整体上确实更强；这说明"未来外生变量"是提升上限的关键来源之一。 DAG 的不同在于：它不仅用未来外生变量，还强调用因果结构（更准确说"因果感知机制"）去组织这些信息，因此在这些强基线之上还能继续领先。

强点 2：跨结构对比下更稳：Transformer、MLP、线性类都比过 基线既包括注意力类（TFT、PatchTST 等）、也包括 MLP/线性类（DLinear 等），还有显式建模交互的 CrossLinear/DUET 等。作者的结论是：DAG 在几乎所有指标上都能压过这些不同结构的路线。 这对读者的启示是：DAG 的收益不是"调参调出来的偶然胜利"，而更像"信息组织方式的系统性改进"。

强点 3：更贴近业务的真实 TSF-X 上，领先更明显 12 个真实 TSF-X 数据集的设定强调"未来外生变量更可信"（近似可知或高度准确），也更符合很多场景：未来日历/计划是确定的，未来环境是可预报的。 在这种情况下，DAG 的第一名次数（26/29）尤其说明它对"未来外生信息"的利用更充分、更稳健。

4.4 作者对"现实限制"的补充实验

如果未来外生变量拿不到怎么办？ 作者在后续实验里专门做了"只用历史外生、不用未来外生"的设定，并说明DAG在推理时可以用(Fθ1)预测出来的(Y^exo)去替代真实(Yexo)并说明 DAG 在推理时可以用 (F_{\theta1}) 预测出来的 (\hat{Y}{exo}) 去替代真实 (Y{exo}) 并说明DAG在推理时可以用(Fθ1)预测出来的(Y^exo)去替代真实(Yexo)，

从而规避"未来外生不可得"。结果表明 DAG 依然表现优秀，这对工程落地是一个加分点。

"DAG 的亮点不在于又发明了一个更大的 Transformer，而在于把未来外生变量从'特征拼接'升级成'结构可迁移的信息源'。"

五、我认为最有价值的3个启发

启发 1：别把"未来外生变量"当成简单特征拼接，它更像另一条可对齐的"未来信息通道"。 论文把未来外生变量的作用分成两层：一层是直接用于预测未来内生（通道模块），另一层是作为学习"可迁移结构"的对象（时间模块先预测未来外生）。这种思路对能源负荷/电价预测很实用：天气预报、负荷预测、风速预报，不只是输入特征，更是你可以"建模其生成机制"的对象。

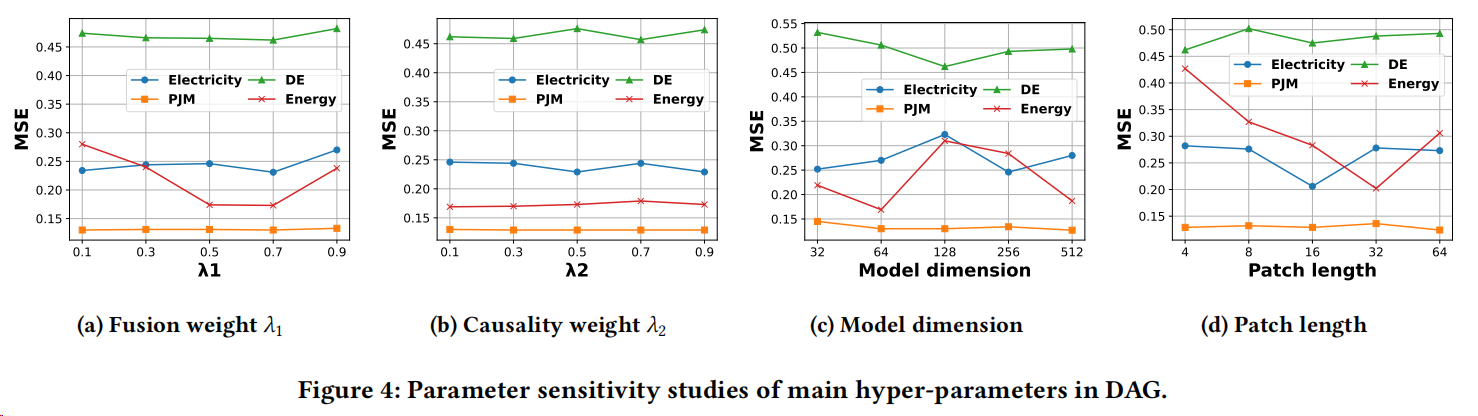
启发 2：用"结构相似性"做迁移，比直接追相关性更稳。 作者用图示强调 temporal/channel 的相似性，并把它落成了"用外生去学注意力的 Q/K，然后注入到目标预测里"。你可以把它理解为：先在更容易学的关系上学到'结构'，再把结构迁移到真正目标上。这对多源协变量的负荷预测尤其友好：目标序列噪声可能更大，但协变量之间的演化更稳定。

启发 3：做 TSF-X 的 ablation 一定要拆"信息源"和"结构约束"。 论文的消融把"只用历史内生""只用未来外生""两者结合""再加 temporal causality / channel causality""最后双因果全量"拆得很清楚，读者可以直接对照：提升到底来自信息源，还是来自结构注入。

六、术语小字典

1. 内生变量（Endogenous）：预测目标本身（如电价、负荷、风机有功功率等），通常由系统内部动态决定。
2. 外生变量（Exogenous / Covariates）：非预测目标但能影响目标的协变量（如天气、日历、负荷/风电预测等）。
3. TSF-X：Time Series Forecasting with Exogenous Variables，指输入包含历史内生、历史外生、以及（可能可得的）未来外生的预测任务设定。
4. Temporal Causality（时间因果）：沿时间维度的依赖结构；论文强调"历史外生→未来外生"的机制与"历史内生→未来内生"的演化相似。
5. Channel Causality（通道/变量因果）：沿变量维度的依赖结构；论文强调"历史外生→历史内生"的关系可迁移到"未来外生→未来内生"。
6. Causal Discovery（因果发现）：在 DAG 里指通过预测任务学习注意力的 Q/K 参数，用作可注入的"因果表征"。
   外生、以及（可能可得的）未来外生的预测任务设定。
7. Temporal Causality（时间因果）：沿时间维度的依赖结构；论文强调"历史外生→未来外生"的机制与"历史内生→未来内生"的演化相似。
8. Channel Causality（通道/变量因果）：沿变量维度的依赖结构；论文强调"历史外生→历史内生"的关系可迁移到"未来外生→未来内生"。
9. Causal Discovery（因果发现）：在 DAG 里指通过预测任务学习注意力的 Q/K 参数，用作可注入的"因果表征"。
10. Causal Injection（因果注入）：把发现阶段得到的 Q/K 参数注入到目标预测分支的注意力计算中，用融合注意力分数约束依赖学习。