本文用通俗易懂的方式讲解了AI背后的三大数学基石:线性代数、微积分和概率统计。线性代数作为"数据容器"和"计算引擎",通过矩阵运算实现高效并行计算;微积分作为"指南针",通过梯度下降算法指引AI优化方向;概率统计作为"水晶球",帮助AI处理不确定性并实现创造性输出。文章通过切菜、调味等生活化比喻,生动阐释了这些数学概念在AI中的实际应用,包括神经网络计算、参数优化和生成式AI创作等核心功能,让读者理解数学如何赋予AI思考和创造的能力。

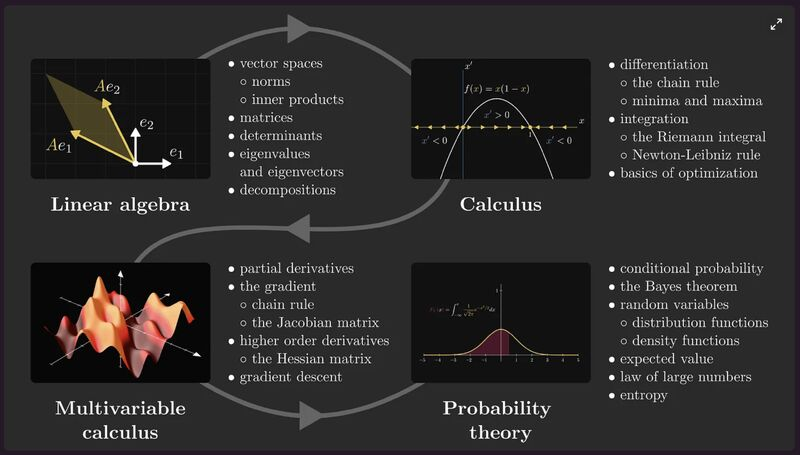

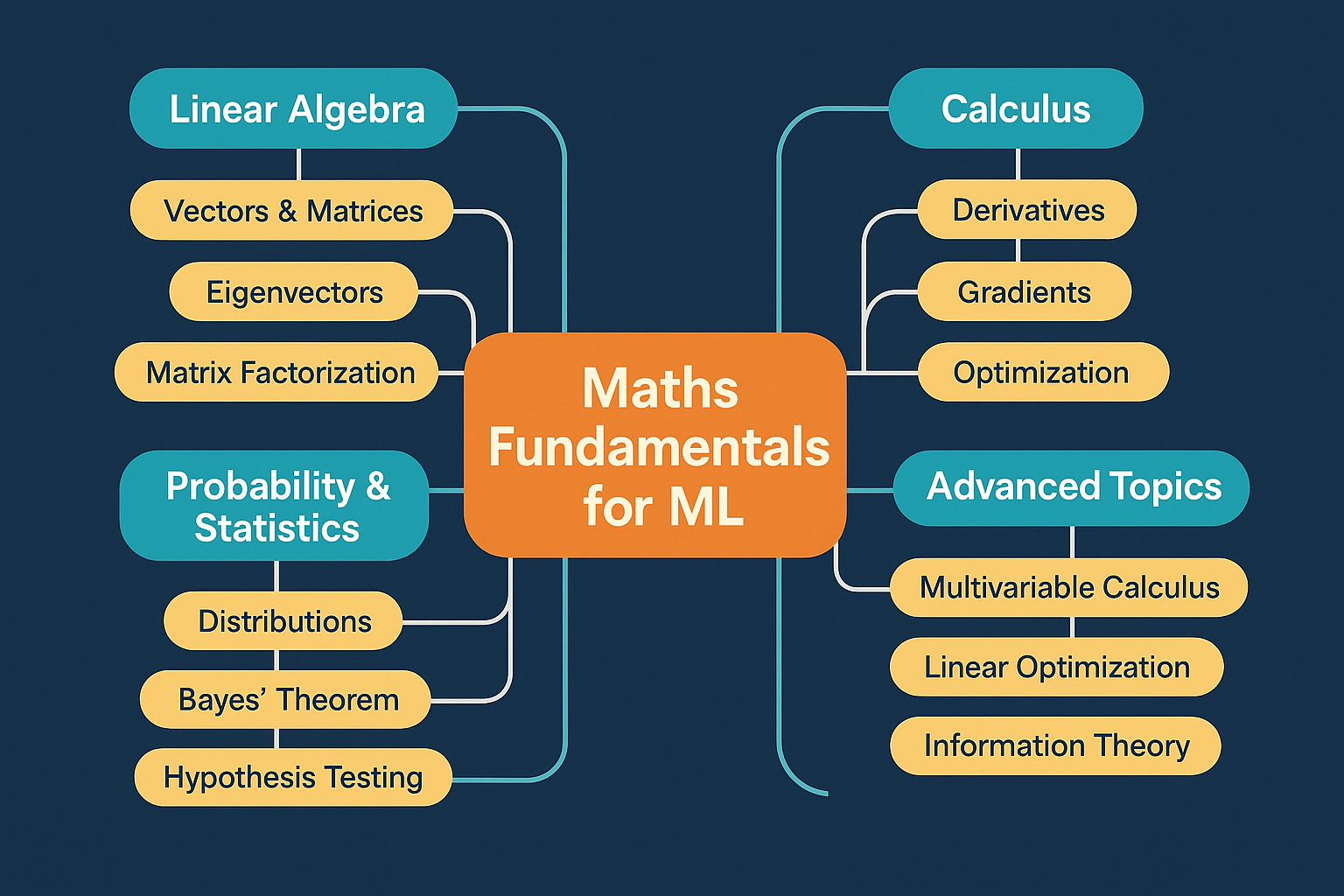
半专业讲解,后面还有大白话讲解
https://www.thepaper.cn/newsDetail_forward_9939482
线性代数 ------ AI 的"数据容器"与"计算引擎"
如果在传统编程中,最重要的数据结构是"数组"和"链表";那么在 AI 编程中,至高无上的神只有一种:张量 (Tensor)。
而线性代数,就是操作张量的说明书。
1. 数据的三种形态:从点到面
在 AI 的眼里,万物皆可数字化。不管是一张照片、一段声音还是一句"我爱你",最终都会变成一堆数字。为了管理这些数字,我们定义了三种容器:
-
标量 (Scalar) ------ 一个点
- 定义: 只有一个单独的数字。
- 例子:
x = 5。 - 在 AI 中: 它可以代表损失函数的值(Loss = 0.02),或者学习率(lr = 0.001)。它没有方向,只有大小。
-
向量 (Vector) ------ 一条线
- 定义: 一排有序的数字。
- 例子:
x = [170, 65]。 - 在 AI 中: 它可以代表一个人的特征:[身高 170cm, 体重 65kg]。或者一个单词在空间中的坐标。
- 几何意义: 它是多维空间中的一个箭头。
-
矩阵 (Matrix) ------ 一个面
- 定义: 一个二维的表格(行 × 列)。
- 例子: 一个 Excel 表格。
- 在 AI 中: 它可以代表一张黑白照片(像素点阵),或者是一次性打包处理的 100 个人的数据。
注: 你以后还会听到 "张量 (Tensor)" 这个词。别怕,它只是通用的叫法:
- 0 阶张量 = 标量
- 1 阶张量 = 向量
- 2 阶张量 = 矩阵
- 3 阶及以上 = 高维数组(比如彩色照片是 3 阶:高 × 宽 × RGB 三通道)
2. 核心运算:矩阵乘法 (Matrix Multiplication)
在神经网络中,90% 的计算量都是矩阵乘法。如果你理解了它,你就理解了 AI 是如何"思考"的。
规则:行 × 列 (Row by Column)
假设我们要计算矩阵 AA 乘以矩阵 BB,得到矩阵 CC。
即 A×B=CA×B=C。
操作步骤:
- 拿出 AA 的第一行。
- 拿出 BB 的第一列。
- 对应元素相乘,然后相加(点积 Dot Product)。
- 这个结果,就是 CC 中第一行第一列的那个数字。
举个栗子(心算一下):
1234\]×\[56\]=\[1324\]×\[56\]= \\begin{bmatrix} ? \\ ? \\end{bmatrix} * **算第一个数:** * 取左边第一行 `[1, 2]`,取右边第一列 `[5, 6]`。 * 计算:1×5+2×6=5+12=171×5+2×6=5+12=17。 * **算第二个数:** * 取左边第二行 `[3, 4]`,取右边第一列 `[5, 6]`。 * 计算:3×5+4×6=15+24=393×5+4×6=15+24=39。 结果就是: $$ \\begin{bmatrix} 17 \\ 39 \\end{bmatrix} $$ > **形状法则 (The Shape Rule) ------ 只要记住这一条,代码就不会报错!** > > 两个矩阵相乘,**中间的维度必须相同**。 > > * (M×N)×(N×K)=(M×K)(M×N)×(N×K)=(M×K) > * 比如:(2×3)(2×3) 的矩阵 乘以 (3×1)(3×1) 的矩阵,结果是 (2×1)(2×1) 的矩阵。 > * 如果维度对不上(比如 2x3 乘以 2x3),程序就会报著名的 `Shape Mismatch Error`。 *** ** * ** *** ##### 3. 为什么 AI 必须要用矩阵? 你可能会问:"我就写个 `for` 循环,一个数一个数地乘不行吗?" **当然可以,但是会慢到让你怀疑人生。** 矩阵运算在 AI 里有两个核心意义: **意义 A:数学上的"加权求和"** 神经网络的本质,就是把输入的信息,赋予不同的**权重 (Weight)** ,然后加起来。 比如预测房价: $$ \\text{房价} = (\\text{面积} \\times w_1) + (\\text{房龄} \\times w_2) $$ 这在数学上,写成向量乘法 W⋅XW⋅X 是最简洁的。 **意义 B:工程上的"并行加速" (Parallelism)** 这是最重要的原因。 想象一下,你要训练一个 AI 识别猫,你有 64 张照片(Batch Size = 64)。 * **CPU (For 循环做法):** 拿起第 1 张照片,算一遍;放下;拿起第 2 张...(串行)。 * **GPU (矩阵做法):** 我把 64 张照片叠在一起,变成一个巨大的矩阵。然后利用矩阵乘法的特性,**一瞬间同时算出 64 张照片的结果**。 **GPU 就是为了做大规模矩阵乘法而生的。** 能够把复杂的数据打包成矩阵,一次性扔给 GPU 算,这就是深度学习能落地的物理基础。 *** ** * ** *** ##### \[代码实战\] Numpy 中的矩阵乘法 在 Python 中,我们不需要手算,只要会调库: Python import numpy as np # 定义数据(输入层) # 假设有 2 个样本,每个样本有 3 个特征 X = np.array([ [1, 2, 3], [4, 5, 6] ]) # 形状: (2, 3) # 定义权重(神经网络的参数) # 3 个输入特征,映射到 1 个输出结果 W = np.array([ [0.1], [0.2], [0.3] ]) # 形状: (3, 1) # 矩阵乘法 (Dot Product) # (2,3) 乘以 (3,1) -> 结果应该是 (2,1) output = np.dot(X, W) print(output) # 结果: # [[1*0.1 + 2*0.2 + 3*0.3] = [1.4] # [4*0.1 + 5*0.2 + 6*0.3]] = [3.2] 看,这就是一次微型的神经网络前向传播!你已经掌握了 AI 的引擎原理。 #### 微积分 ------ AI 的"指南针"与"纠错器" 如果说线性代数构建了 AI 的身体(骨架与肌肉),那么微积分就赋予了 AI **学习的能力**。 没有微积分,AI 就是一个静止的雕塑;有了微积分,它才能动起来,去自我优化。 ##### 1. 直觉理解:什么是导数 (Derivative)? 抛开课本上复杂的极限定义 limΔx→0limΔx→0,在 AI 的世界里,导数只有两个含义: 1. **敏感度 (Sensitivity):** 如果你轻轻推了一下输入 xx(让它变化一点点),输出 yy 会跟着变化多少? * 如果导数很大,说明 yy 对 xx 非常敏感(一触即跳)。 * 如果导数是 0,说明 yy 根本不在乎 xx 怎么变(麻木不仁)。 2. **方向 (Direction):** 如果我想让 yy 变小,我应该把 xx 调大一点,还是调小一点? * 导数为正(斜率向上):xx 变大,yy 也变大。→→ 想让 yy 变小,就要减小 xx。 * 导数为负(斜率向下):xx 变大,yy 反而变小。→→ 想让 yy 变小,就要增大 xx。 **记住这句话:导数告诉了我们,参数该往哪个方向调,才能让误差变小。** *** ** * ** *** ##### 2. 核心场景:梯度下降 (Gradient Descent) 这是深度学习中**最最最**重要的算法。没有之一。 想象一下,你被蒙住双眼,空投到了崇山峻岭之中(这个山脉就是**损失函数 Loss Function** ,高度代表**误差** )。 你的目标是:**活着走到山谷的最低点**(误差最小化)。 **你该怎么办?** 1. **感知(求导):** 用脚探一探周围。感觉到左边地势变高了,右边地势变低了(这就是计算梯度的过程)。 2. **决策(更新):** 既然右边低,那就往右边迈一步。 3. **循环(迭代):** 再探,再走。直到你感觉到四周都比脚下高(导数为 0),说明你到谷底了。 **数学公式就一行:** $$ w_{\\text{new}} = w_{\\text{old}} - \\text{lr} \\times \\frac{\\partial \\text{Loss}}{\\partial w} $$ * ww:我们要训练的参数(权重)。 * ∂Loss∂w∂w∂Loss:**梯度(导数)**。它告诉我们山坡有多陡,以及下坡的方向。 * lrlr (Learning Rate):**学习率**。它决定了你一步迈多大。 * **为什么是减号?** 因为梯度指向的是"最陡峭的上坡方向",我们要下山,所以要**反着走**。 *** ** * ** *** ##### 3. 进阶概念:偏导数与链式法则 虽然我们说不讲复杂数学,但这两个概念必须得提,因为它们是**反向传播 (Backpropagation)** 的基石。 **A. 偏导数 (Partial Derivative) ------ 控制变量法** 神经网络有成千上万个参数(w1,w2,...w1,w2,...)。当我们想调整 w1w1 时,必须假装其他参数(w2,w3...w2,w3...)都是死木头,暂时不动。 * 符号从 dd 变成了 ∂∂(读作 "del" 或 "partial")。 * 含义:**"在只有我变、别人都不变的情况下,我对结果有多大影响?"** **B. 链式法则 (Chain Rule) ------ 冤有头债有主** 神经网络是一层叠一层的(像千层饼)。 输入 x→x→ 第一层 →→ 第二层 →→ ... →→ 误差 LossLoss。 如果 LossLoss 太大,到底是谁的错?是最后一层没算好?还是第一层就传错了? 链式法则就是\*\*"连坐制度"\*\*: $$ \\frac{\\partial \\text{Loss}}{\\partial x} = \\frac{\\partial \\text{Loss}}{\\partial \\text{Layer}_2} \\times \\frac{\\partial \\text{Layer}_2}{\\partial \\text{Layer}_1} \\times \\frac{\\partial \\text{Layer}_1}{\\partial x} $$ 它像传声筒一样,把误差的信号,从最后一层,一层一层地**反向传递** 回第一层。 这就是**反向传播**的数学本质:利用链式法则,算出每一个神经元对错误的"贡献度",然后精准地惩罚它(调整它的权重)。 *** ** * ** *** ##### \[实战演示\] PyTorch 中的自动求导 好消息是,现代 AI 框架(如 PyTorch)已经帮我们搞定了所有求导工作。这种技术叫 **Autograd(自动微分)**。你只需要写前向传播(怎么算的),PyTorch 会自动把反向传播(怎么求导)给你写好。 Python import torch # 1. 定义一个参数 x,初始化为 2.0 # requires_grad=True 意味着:我们要追踪这个变量的导数 x = torch.tensor(2.0, requires_grad=True) # 2. 定义一个函数(模拟 Loss) # y = x^2 + 3x y = x**2 + 3*x # 此时 y = 2^2 + 3*2 = 10 # 3. 自动求导(反向传播) # 这一步,PyTorch 已经在后台用链式法则算好了导数 y.backward() # 4. 查看导数 # 数学计算:y' = 2x + 3 # 代入 x=2:y' = 2*2 + 3 = 7 print(x.grad) # 输出:tensor(7.) 看,你不需要手算导数。你只需要理解:**`backward()` 就是在命令 PyTorch 去山坡上探路。** 在传统的编程世界里,`1+1` 必须等于 `2`;但在 AI 的世界里,我们将学会接受:`1+1` 也就是大概率等于 `2`,有时候可能是 `1.99`,有时候甚至是"我不知道"。 #### 概率统计 ------ AI 的"水晶球"与"造梦术" 传统软件开发建立在\*\*逻辑(Logic)**之上,非黑即白。 AI 开发建立在**概率(Probability)\*\*之上,充满了灰度。 如果你问一个 AI:"照片里这只动物是猫吗?" 它不会回答"是"或"否"。 它会回答:"我有 **98.2%** 的把握它是猫,还有 **1.8%** 的可能是只像猫的小狗。" 要听懂 AI 的这种"模糊语言",你需要掌握三个核心概念。 ##### 1. 数据的"中心"与"范围":期望与方差 当你训练 AI 时,你实际上是在处理成千上万个数据点。我们不可能盯着每一个点看,我们需要用两个指标来概括它们: * **期望 (Expectation / Mean, μμ):** * **直觉:** 平均值,或者说"大多数数据聚集的地方"。 * **AI 场景:** 预测房价时,模型输出的那个价格,本质上是它对真实价格的**期望**。 * **方差 (Variance, σ2σ2):** * **直觉:** 离散程度,或者说"数据有多乱"。 * **AI 场景:** * **方差小:** 数据都很守规矩,挤在平均值旁边(好学)。 * **方差大:** 数据到处乱跑,忽大忽小(难学,噪声大)。 * *注:标准差 (Standard Deviation, σσ) 是方差的平方根,更常用,因为它和数据的单位一致。* > **射击的比喻:** > > * **期望** 决定了你打出的子弹**平均落在哪里**(是不是瞄准了靶心)。 > * **方差** 决定了你的**手有多抖**(子弹是聚在一起,还是散得满墙都是)。 > * **最好的 AI 模型:** 期望对准靶心(偏差小),且方差极小(极其稳定)。 *** ** * ** *** ##### 2. 上帝的曲线:正态分布 (Normal Distribution) 在数学界,只有一种分布能被称为"正态"(Normal,意为正常的、标准的),可见它的地位。它也叫**高斯分布 (Gaussian Distribution)**。 * **形状:** 著名的**钟形曲线 (Bell Curve)**。中间高,两边低,左右对称。 * **含义:** 绝大多数数据都聚集在中间(均值附近),极少数极端数据在两边(长尾)。 * **为什么 AI 离不开它?** 1. **大自然的规律:** 人类的身高、考试的成绩、传感器的噪声,天然都服从正态分布。AI 既然要模拟真实世界,就必须用这个模型。 2. **初始化的默认值:** 当我们刚开始创建一个神经网络时,参数(权重)不能全是 0。我们通常会从正态分布中随机抽取一些小数来赋值。这叫 **"高斯初始化"**。 *** ** * ** *** ##### 3. 为什么需要概率?从"判别"到"生成" 这是本章最重要的部分。概率不仅仅是用来描述数据的,它更是现代 AI **创造力**的源泉。 **A. 判别式 AI (Discriminative AI) ------ 处理不确定性** * **任务:** 给你一张图,分类是猫还是狗。 * **原理:** 神经网络的最后一层通常是一个 **Softmax** 函数。它把输出变成了一组概率分布。 * Output: `[猫: 0.9, 狗: 0.1]` * 这意味着 AI 承认了世界的不确定性。它不说绝对的话,只给可能性的建议。 **B. 生成式 AI (Generative AI) ------ 扩散模型的魔法** 你一定听说过 Stable Diffusion 或 Midjourney。它们是怎么凭空画出一幅画的? **答案就是:玩弄正态分布。** * **扩散模型 (Diffusion Model) 的原理:** 1. **加噪(毁图):** 把一张清晰的蒙娜丽莎照片,一点点加上符合**正态分布** 的噪点(雪花点)。最后,图片变成了一张纯粹的、毫无意义的**高斯噪声图**。 2. **去噪(画图):** AI 学习的是**逆向过程**。给它一张全是噪点的图,让它猜测:"如果我想把这堆噪点还原成一幅画,我该减去什么样的噪声?" 3. **创造:** 当你让 AI 画画时,它其实是从**纯随机的正态分布噪声**中,一步步"雕刻"出图像的。 > **一句话总结:** > > 如果没有概率论中的正态分布,AI 就无法理解什么是"噪声",也就无法从噪声中创造出惊艳的艺术作品。 *** ** * ** *** ##### \[代码实战\] 用 PyTorch 制造一点"混乱" 让我们看看如何在 Python 中生成正态分布数据,这在任何 AI 项目的开头都是必做步骤。 Python import torch import matplotlib.pyplot as plt # 1. 生成一个标准正态分布的张量 # mean(均值) = 0, std(标准差) = 1 # 形状为 1000 个点 noise = torch.randn(1000) # 2. 打印看看 print(f"期望 (均值): {noise.mean().item():.4f}") # 结果应该非常接近 0,比如 0.012 print(f"方差: {noise.var().item():.4f}") # 结果应该非常接近 1,比如 0.985 # 3. 看看前5个数据 # 这些数据就是神经网络权重的"初始状态" print(f"随机权重: {noise[:5]}") # 输出示例: tensor([-0.12, 1.45, -0.03, 0.88, -1.21]) 当你运行这段代码时,你其实是在模拟上帝掷骰子。而 AI 的训练过程,就是要把这些随机杂乱的骰子,排列成有序的智慧结构。 ### 用"大白话"再讲一遍这三个数学基石 想象你在**做菜**(训练 AI) #### 1. 线性代数 = 切菜与装盘(批量处理) * **学术说法**:标量、向量、矩阵运算。 * **人话版** :**这就是一种"打包批发"的高效计算方法。** 想象你要处理 100 根胡萝卜(数据)。 * **没有线性代数(标量思维)** :你拿一根胡萝卜,切一刀;放下;再拿第二根,切一刀......(累死你,也就是 CPU 传统的 `for` 循环模式)。 * **有了线性代数(矩阵思维)** :你把 100 根胡萝卜整整齐齐码在一起,变成一个长方形的方阵(这就是**矩阵** )。然后你拿一把 40 米长的大刀,**咔嚓一下**,这 100 根胡萝卜同时被切好了。 **核心作用** : **省时间。** 显卡(GPU)就是那把 40 米大刀,它最擅长这种"咔嚓一下全部算完"的操作。如果你不懂把数据打包成矩阵,显卡这把大刀就没法用,AI 训练就要跑几百年。 *** ** * ** *** #### 2. 微积分 = 尝味与调料(指引方向) * **学术说法**:导数、梯度下降。 * **人话版** :**这就是在问:"如果我把火开大一点点,这道菜会更好吃还是更难吃?"** 你在炖一锅汤(训练模型),目标是让汤变好喝(误差变小)。 * **什么是导数?** 你尝了一口,觉得淡了。你心想:"如果我现在**多加一勺盐** (参数变化),汤的味道会**变咸多少** (结果变化)?" 这个\*\*"变咸多少"\*\*的感觉,就是导数。 * **什么是梯度下降?** * 如果导数告诉你:加盐会让汤更好喝 →→ 那你就**加盐**。 * 如果导数告诉你:加盐会让汤齁死 →→ 那你就**少加盐**(或者加水)。 * 你要做的就是不断地:**尝一口 →→ 算算该加还是该减 →→ 动手调一点 →→ 再尝一口**。 * 一直调到汤的味道完美为止。 **核心作用** : **给 AI 导航。** 告诉 AI 现在的参数是太大了还是太小了,下一步该往哪个方向改。 *** ** * ** *** #### 3. 概率统计 = 猜谜与容错(处理不确定) * **学术说法**:正态分布、期望、方差。 * **人话版** :**这就是承认"差不多得了",别钻牛角尖。** 在这个世界上,很多事情是没有 100% 确定答案的。 * **什么是概率分布?** 你问 AI:"这张模糊的照片里是人吗?" AI 不会死板地说"是"或"不是"。它会像个老练的算命先生:"我有 90% 的把握是人,但看这轮廓,也有 10% 的可能是一把拖把。" 这种**给自己留后路**的说话方式,就是概率分布。 * **什么是正态分布(高斯分布)?** 这就是\*\*"随大流"\*\*。 比如全班考试,大多数人(中间最高的那个峰)都考 70-80 分,考 0 分和考 100 分的都是极少数(两边低)。 AI 在刚开始学习或者生成图片时,会假设所有数据都长这副德行(随大流),然后再慢慢调整。 **核心作用** : **让 AI 拥有创造力和抗干扰能力。** 正是因为有概率,AI 生成的画作才每次都不一样(创造力);也正是因为有概率,AI 看到一张稍微有点脏的猫照片,也能认出是猫,而不是报错(抗干扰)。 *** ** * ** *** #### 总结一下 做一道名为"AI"的菜: 1. **线性代数** 帮你把几吨食材一次性**切好**(高效计算)。 2. **微积分** 告诉你现在的火候不对,该**往大调还是往小调**(自我修正)。 3. **概率统计** 让你在最后摆盘时,允许有一点点**随机的艺术感**,而不是像机器人一样死板(处理不确定性)。
