学的这个课程
算是强化学习里面很火的课程了(ﾟ∀ﾟ)
老师的讲义和书都是英文的，可以看看啊，词汇都不难，主要是理解一些专业词汇
这个是第三章里面压缩映射定理的证明，正好学习一下Latex
CSDN里面公式显示好像不太稳定，可以直接去看书
1. we prove that the sequence 
with is convergent.
the proof relies on Cauchy sequences: for any small , there exists
such that
for all
if we simply have , it is insufficient to claim that the sequence is a Cauchy sequence. For example, it holds that
for
, but apparently, it diverges.
we next show that is a Cauchy sequence and hence converges.
first, since is a contraction mapping, we have
thus,we have
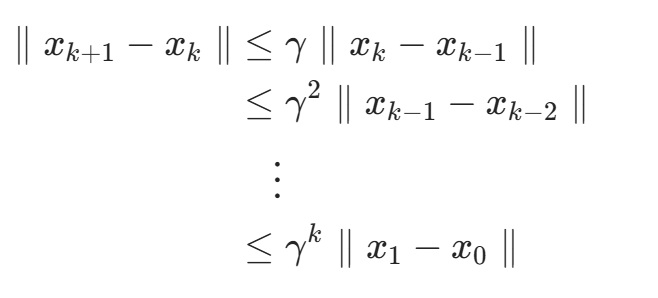
since ,we know that
converges to zero exponentially fast as
given any
we need to futher consider for any
. In particular,
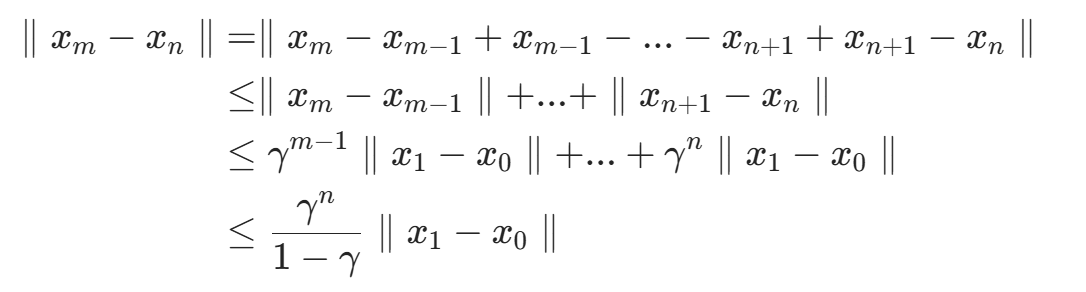
Therefore, this sequence is Cauchy and hence converges to a limit point denoted as
2. we show that the limit is a fixed point.
converges to zero exponentially fast
3. we show that the fixed point is unique.
suppose that there is another fixed point , then
this inequality holds if and only if . therefore,