控制系统建模仿真（十）:实战篇——从工具掌握到工程化落地

前言

欢迎进入实战习题演练环节。

如果说前面的九个章节是让你在"武器库"中逐一挑选并熟悉各种精良的装备，那么从这一刻起，你将正式踏上战场。

控制系统的设计从来不是孤立的。在真实的工程挑战中，你不会只用到一个 tf 函数或一个 Step 模块。你需要像一位经验丰富的指挥官，在面对一个物理对象时，迅速调用第四章的建模能力 进行"画像"，利用第五、六章的分析工具 进行"体检"，最后综合第七、八章的设计方案给予"治疗"。

本环节我们将全面调动 MATLAB 的脚本编程逻辑与 Simulink 的动态仿真能力，去解决那些真正令工程师头疼的实际问题。理论的生命力在于实践，让我们开始这场由数字通往现实的最后征途。

第一题：M 函数实现 for/while 循环计算

一、解题思路

核心目标是通过两种循环结构（for/while）实现"累加k的k次方"，步骤拆解如下：

函数框架设计 ：定义M函数 fun(n)，输入参数为求和上限 n，输出两个结果（分别对应for/while循环），方便验证一致性。
for循环逻辑 ：
- 初始化累加变量为0（避免初始垃圾值影响结果）；
- 循环变量 k 遍历1到n，每次将 k^k 累加到累加变量中（利用MATLAB的 ^ 运算符实现幂运算）。
while循环逻辑 ：
- 同样初始化累加变量为0，额外初始化循环变量 k=1；
- 以 k<=n 为循环条件，每次累加 k^k 后，手动将 k 自增1（否则会陷入死循环）。
测试验证 ：调用函数传入 n=20，输出两种方法的结果，确认一致即正确。

二、完整代码

1. M函数文件（需保存为 `fun.m`，与MATLAB工作目录一致）

matlab 复制代码

function [y_for, y_while] = fun(n)
    % --------------- for循环实现 ---------------
    y_for = 0;  % 初始化累加变量（必须从0开始）
    for k = 1:n  % 循环变量k：1→2→...→n（步长默认1）
        y_for = y_for + k^k;  % 累加k的k次方（^是幂运算）
    end
    
    % --------------- while循环实现 ---------------
    y_while = 0;  % 初始化累加变量
    k = 1;        % 初始化循环变量（起始值1）
    while k <= n  % 循环条件：k不超过n时继续
        y_while = y_while + k^k;  % 累加操作
        k = k + 1;  % 循环变量自增（关键！避免死循环）
    end
end

2. 测试代码（在MATLAB命令行或脚本中运行）

matlab 复制代码

% 调用函数计算n=20时的结果
[n20_for, n20_while] = fun(20);

% 输出结果（%g自动优化显示格式，适配大数值）
fprintf('for循环计算n=20的结果：%g\n', n20_for);
fprintf('while循环计算n=20的结果：%g\n', n20_while);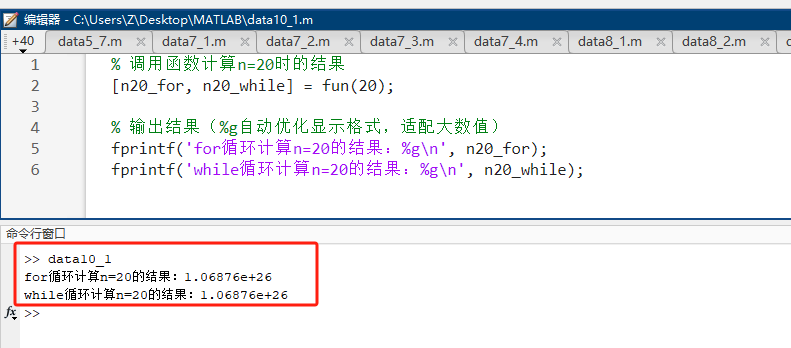

第二题：非线性约束最小优化

一、解题思路

一、问题背景：待求解的优化问题

先明确我们要解决的核心问题，目标函数和约束条件如下：

1. 目标函数（最小化）
f(s,t)=s4+4s−8t+15 f(s,t) = s^4 + 4s - 8t + 15 f(s,t)=s4+4s−8t+15

其中 s、ts、ts、t 是优化变量。

2. 约束条件

变量下界约束：s≥1，t≥2s \geq 1，t \geq 2s≥1，t≥2（对应代码中lb=[1,2]）；
线性不等式约束：
{2s+3t≤2t−s≤5 \begin{cases} 2s + 3t \leq 2 \\ t - s \leq 5 \end{cases} {2s+3t≤2t−s≤5
非线性不等式约束：
s2+t2≥9 s^2 + t^2 \geq 9 s2+t2≥9

fmincon是MATLAB Optimization Toolbox中求解有约束非线性最小化问题 的专用函数，核心逻辑是：
定义目标函数 → 定义所有约束 → 设置初始点/变量边界 → 调用fmincon求解 → 输出结果

matlab 复制代码

[x, fval, exitflag, output] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)

每个参数的详细含义

按参数顺序逐一解释，表格+文字结合，重点标注你代码中用到的参数：

参数名	核心含义	数据类型/格式	你的案例取值/说明
`fun`	需最小化的目标函数（核心）	函数句柄（@函数名）/匿名函数	`@fun2`：对应目标函数 f(s,t)=s4+4s−8t+15f(s,t)=s^4+4s-8t+15f(s,t)=s4+4s−8t+15，输入是向量`x=[s,t]`，输出是标量fff
`x0`	优化算法的初始迭代点（必须指定）	n维向量（n=变量数）	`[1,2]`：对应变量s=1、t=2s=1、t=2s=1、t=2，是迭代的起点（非线性优化初始点可能影响结果）
`A`	线性不等式约束 A⋅x≤bA·x ≤ bA⋅x≤b 的系数矩阵	m×n矩阵（m=约束数，n=变量数）	`[]`：将线性约束放到了`nonlcon`中，故设为空；若单独写，如 2s+3t≤22s+3t≤22s+3t≤2 则`A=[2,3]`
`b`	线性不等式约束 A⋅x≤bA·x ≤ bA⋅x≤b 的右端项向量	m×1向量	`[]`：无单独的线性不等式约束，故设为空
`Aeq`	线性等式约束 Aeq⋅x=beqAeq·x = beqAeq⋅x=beq 的系数矩阵	p×n矩阵（p=等式约束数）	`[]`：问题无线性等式约束（如s+t=5s+t=5s+t=5），故设为空
`beq`	线性等式约束 Aeq⋅x=beqAeq·x = beqAeq⋅x=beq 的右端项向量	p×1向量	`[]`：无线性等式约束，故设为空
`lb`	优化变量的下界（x≥lbx ≥ lbx≥lb）	n维向量	`[1,2]`：对应s≥1、t≥2s≥1、t≥2s≥1、t≥2；若某变量无下界，可设为`-inf`（如s≥−∞s≥-∞s≥−∞则`lb(1)=-inf`）
`ub`	优化变量的上界（x≤ubx ≤ ubx≤ub）	n维向量	`[]`：你的问题无上界约束；若某变量无上界，可设为`inf`（如t≤∞t≤∞t≤∞则`ub(2)=inf`）
`nonlcon`	非线性约束函数句柄（返回不等式约束g(x)≤0g(x)≤0g(x)≤0、等式约束h(x)=0h(x)=0h(x)=0）	函数句柄（@函数名）	`@fun3`：返回g=[−s2−t2+9;2s+3t−2;s−t−5]g=[-s²-t²+9;2s+3t-2;s-t-5]g=[−s2−t2+9;2s+3t−2;s−t−5]（均≤0），h=[]h=[]h=[]（无非线性等式约束）
`options`	优化选项（算法、显示模式、迭代次数等）	优化选项对象（optimoptions）	`optimoptions('fmincon','Display','iter','Algorithm','sqp')`：显示迭代、用SQP算法

二、完整代码

代码一：

matlab 复制代码

function f=fun2(x)
    f=x(1)^4+4*x(1)-8*x(2)+15;
end

代码二：

matlab 复制代码

function [g,h]=fun3(x)
    g=[-x(1)^2-x(2)^2+9;
        2*x(1)+3*x(2)-2;
        x(1)-x(2)-5];
    h=[];
end

代码三：

matlab 复制代码

x0=[1,2];
lb=[1,2];
options=optimoptions('fmincon','Display','iter','Algorithm','sqp');
[x,fval]=fmincon('fun2',x0,[],[],[],[],lb,[],'fun3',options);
disp("最优解为");
disp(x);
disp("最优值为");
disp(fval)

三、运行结果

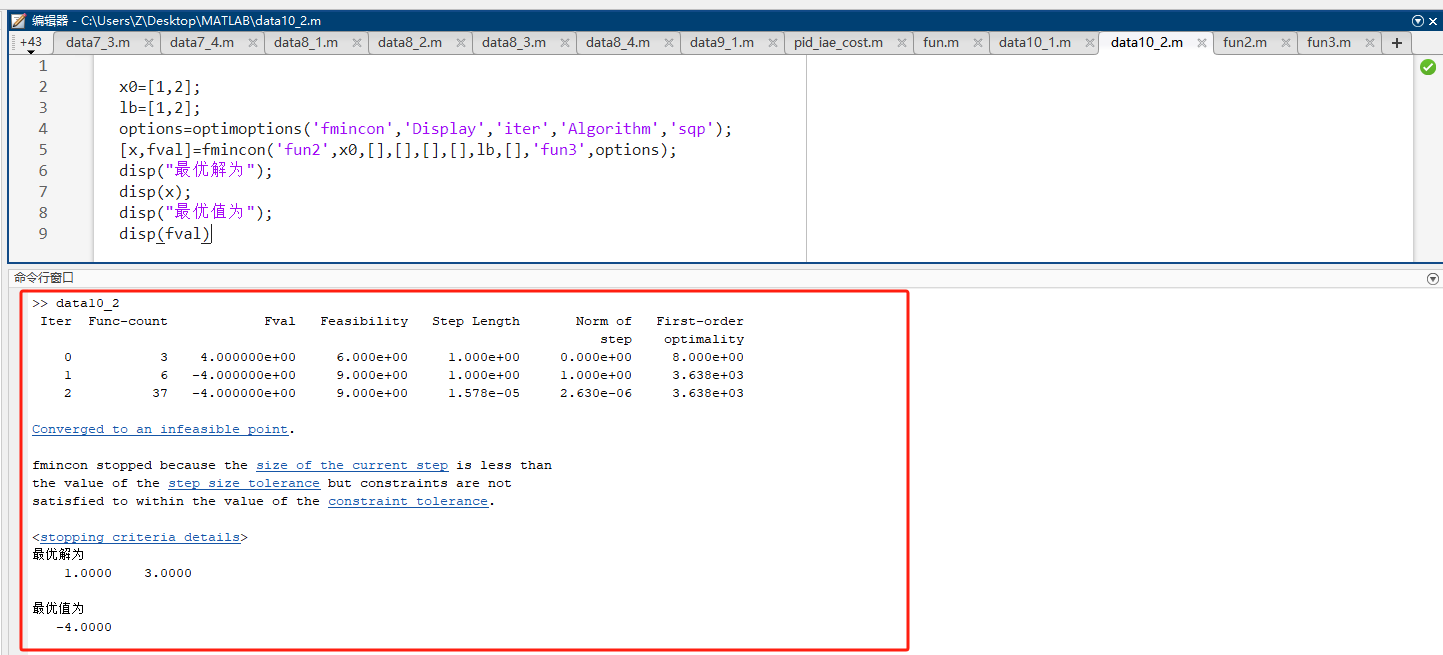
第三题：求解线性方程组

一、解题思路

提取系数矩阵 ( \boldsymbol{A} )：将每个方程的未知数系数按行排列（注意：缺失的未知数系数填0，如第二个方程的 ( x_3 ) 系数为0）；
提取常数项向量 ( \boldsymbol{b} )：将每个方程的右端常数按顺序排列；
求解方程组 ：用 x = A\b 计算未知数向量；
输出结果：打印求解得到的 ( x_1, x_2, x_3, x_4 )。

二、完整代码

matlab 复制代码

% ---------------------- 求解四元线性方程组 ----------------------
clc; clear;  % 清空命令行和工作区，避免干扰

% 1. 定义系数矩阵A（4行4列，对应4个方程、4个未知数）
% 方程1：2x1 -3x2 +1x3 +2x4 =8 → 行1：[2, -3, 1, 2]
% 方程2：1x1 +3x2 +0x3 +1x4 =6 → 行2：[1, 3, 0, 1]（x3系数为0）
% 方程3：1x1 -1x2 +1x3 +8x4 =1 → 行3：[1, -1, 1, 8]
% 方程4：7x1 +1x2 -2x3 +2x4 =5 → 行4：[7, 1, -2, 2]
A = [
    2, -3, 1, 2;
    1,  3, 0, 1;
    1, -1, 1, 8;
    7,  1, -2, 2
];

% 2. 定义常数项向量b（4行1列，对应每个方程的右端常数）
b = [8; 6; 1; 5];

% 3. 求解线性方程组：A*x = b → x = A\b
x = A \ b;

% 4. 输出结果（保留4位小数，增强可读性）
fprintf('线性方程组的解为：\n');
fprintf('x1 = %.4f\n', x(1));
fprintf('x2 = %.4f\n', x(2));
fprintf('x3 = %.4f\n', x(3));
fprintf('x4 = %.4f\n', x(4));

三、运行结果

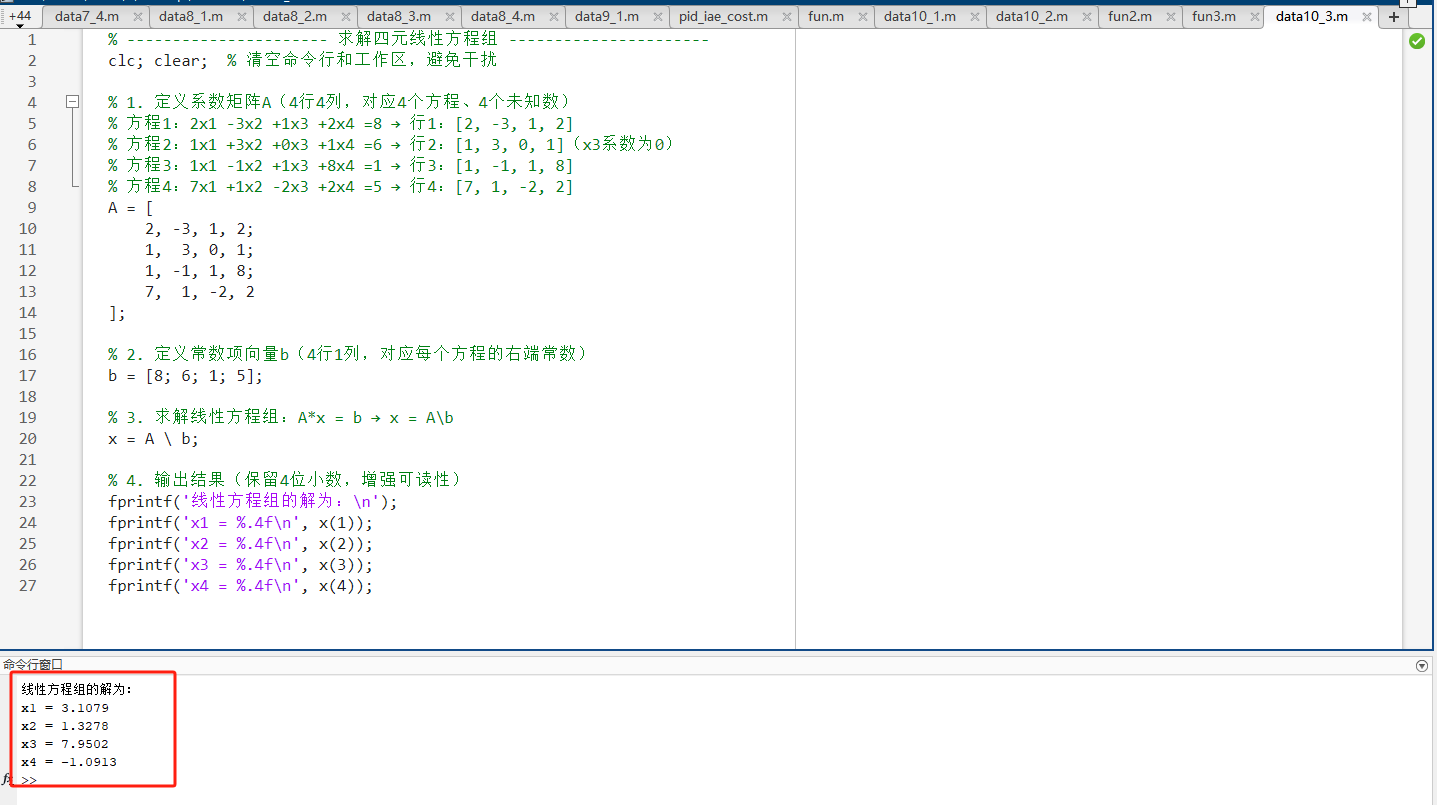
第四题：响应曲线建模

一、解题思路

响应计算：根据题目给出的二阶系统时域响应公式，生成0~10s的时间序列，对每个阻尼比(\zeta)（0.1、0.5、0.8）计算对应的响应曲线(y(t))；
绘图要求：在同一图中绘制三条曲线，分别用指定颜色/线型区分，并添加标注；
性能指标 ：通过MATLAB函数（或逻辑判断）计算每条曲线的上升时间 （从0到稳态值的时间）、峰值时间 （第一个峰值的时间）、超调量（峰值与稳态值的偏差百分比）。

二、完整代码

matlab 复制代码

function test()
    % 二阶系统时域响应仿真与性能指标计算
    % ---------------------- 1. 初始化参数 ----------------------
    t = 0:0.01:10;  % 仿真时间：0~10s，步长0.01s（保证曲线平滑）
    zeta_list = [0.1, 0.5, 0.8];  % 待分析的阻尼比
    y = zeros(length(t), length(zeta_list));  % 存储3条响应曲线（行：时间点，列：阻尼比）

    % ---------------------- 2. 计算各阻尼比的时域响应 ----------------------
    for i = 1:length(zeta_list)
        zeta = zeta_list(i);  % 当前阻尼比
        sigma = zeta * pi;    % 衰减系数（对应题目公式中的-ζπt）
        omega_d = sqrt(1 - zeta^2);  % 阻尼振荡频率
        phi = acos(zeta);     % 相位角（对应公式中的arccosζ）
        
        % 按题目公式计算响应（点运算适配向量t）
        y(:,i) = 1 - (1/omega_d) .* exp(-sigma .* t) .* sin(omega_d .* t + phi);
    end

    % ---------------------- 3. 绘制响应曲线 ----------------------
    figure('Name','二阶系统时域响应（不同阻尼比）');
    hold on; grid on;  % 保留曲线+显示网格
    
    % 绘制3条曲线（对应不同阻尼比，设置颜色/线型）
    plot(t, y(:,1), 'b-', 'LineWidth', 1.5);   % ζ=0.1：蓝色实线
    plot(t, y(:,2), 'g-.', 'LineWidth', 1.5);  % ζ=0.5：绿色点划线
    plot(t, y(:,3), 'r--', 'LineWidth', 1.5);  % ζ=0.8：红色虚线
    
    % 标注信息（图例、标题、坐标轴）
    legend(['ζ=', num2str(zeta_list(1))], ['ζ=', num2str(zeta_list(2))], ['ζ=', num2str(zeta_list(3))], 'Location','best');
    title('二阶系统单位阶跃响应（不同阻尼比）');
    xlabel('时间 t (s)');
    ylabel('输出 y(t)');
    hold off;

    % ---------------------- 4. 计算性能指标（上升时间、峰值时间、超调量） ----------------------
    fprintf('===== 二阶系统性能指标（不同阻尼比） =====\n');
    for i = 1:length(zeta_list)
        zeta = zeta_list(i);
        yi = y(:,i);  % 当前阻尼比的响应曲线
        
        % （1）上升时间Tr：第一次到达稳态值（1）的时间（取y≥0.99的第一个时刻）
        idx_rise = find(yi >= 0.99, 1, 'first');  % 找第一个满足条件的索引
        Tr = t(idx_rise);
        
        % （2）峰值时间Tp：第一个峰值对应的时间（用findpeaks找极大值）
        [pks, locs] = findpeaks(yi);  % 提取所有峰值的"值"和"索引"
        if ~isempty(pks)  % 欠阻尼系统（ζ<1）必有峰值
            Tp = t(locs(1));  % 第一个峰值的时间
            PO = (pks(1) - 1) * 100;  % 超调量（%，公式：(峰值-稳态值)/稳态值×100%）
        else
            Tp = NaN; PO = 0;  % 临界/过阻尼无峰值（本题ζ<1，不会执行）
        end
        
        % 输出结果
        fprintf('ζ=%.1f 时：\n', zeta);
        fprintf('  上升时间 Tr = %.2f s\n', Tr);
        fprintf('  峰值时间 Tp = %.2f s\n', Tp);
        fprintf('  超调量 PO = %.2f %%\n\n', PO);
    end
end

三、运行结果

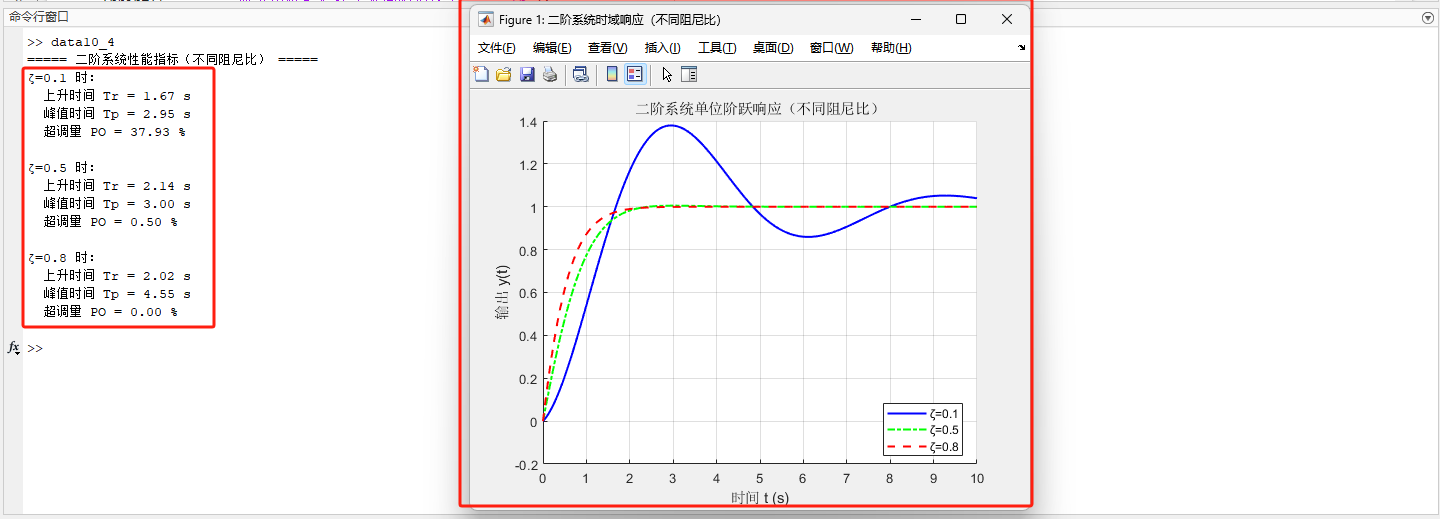
第五题：稳定性判别

一、解题思路

构建开环传递函数 ：根据题目给出的开环传递函数 ( G(s) = \frac{10}{s(s+1)(s+5)} )，分解分子、分母的多项式系数，用tf()函数创建传递函数对象；
绘制Bode图 ：用bode()函数直接绘制系统的幅频特性和相频特性曲线；
计算稳定裕度 ：用margin()函数提取幅值裕度 （Gm）和相角裕度（Pm）（稳定裕度是判断系统稳定性的核心指标）；
判断稳定性 ：若相角裕度Pm>0° 且幅值裕度Gm（dB）>0dB，系统稳定；否则不稳定。

二、完整代码

matlab 复制代码

% ---------------------- 单位负反馈系统的Bode图与稳定裕度分析 ----------------------
% 1. 构建开环传递函数 G(s) = 10/[s(s+1)(s+5)]
num = [10];  % 分子多项式系数（10对应s^0项）
den = [1, 6, 5, 0];  % 分母多项式系数：s(s+1)(s+5) = s³+6s²+5s → 系数为[1,6,5,0]
G = tf(num, den);  % 创建开环传递函数对象
disp('开环传递函数 G(s)：');
disp(G);

% 2. 绘制系统的Bode图
figure('Name','系统Bode图（含稳定裕度）');
bode(G);  % 绘制幅频+相频特性曲线
grid on;  % 显示网格（便于读取数据）
title('开环传递函数 Bode图（幅值裕度+相角裕度）');

% 3. 计算幅值裕度、相角裕度
[Gm, Pm, Wcg, Wcp] = margin(G);  % 提取稳定裕度
% 转换幅值裕度为dB（默认Gm是线性值，工程中常用dB表示）
Gm_dB = 20*log10(Gm);

% 4. 输出稳定裕度并判断稳定性
fprintf('\n===== 系统稳定裕度 =====\n');
fprintf('幅值裕度（线性值）：Gm = %.2f\n', Gm);
fprintf('幅值裕度（dB）：Gm_dB = %.2f dB\n', Gm_dB);
fprintf('相角裕度：Pm = %.2f °\n', Pm);
fprintf('相角穿越频率（Wcg）：%.2f rad/s\n', Wcg);
fprintf('幅值穿越频率（Wcp）：%.2f rad/s\n', Wcp);

% 判断稳定性
if Pm > 0 && Gm_dB > 0
    fprintf('\n系统稳定性：稳定\n');
else
    fprintf('\n系统稳定性：不稳定\n');
end

三、运行结果

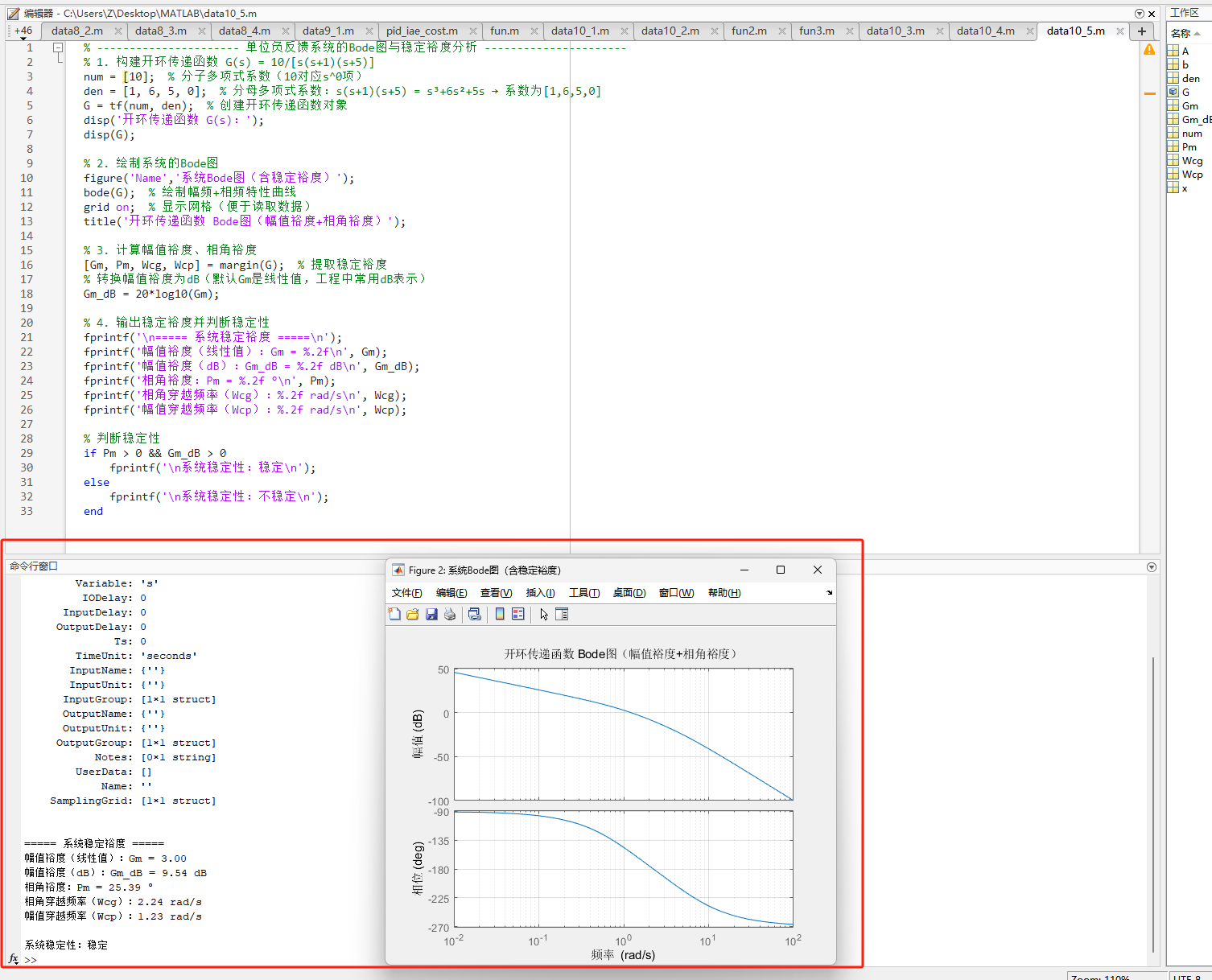
第六题：实时控制系统设计

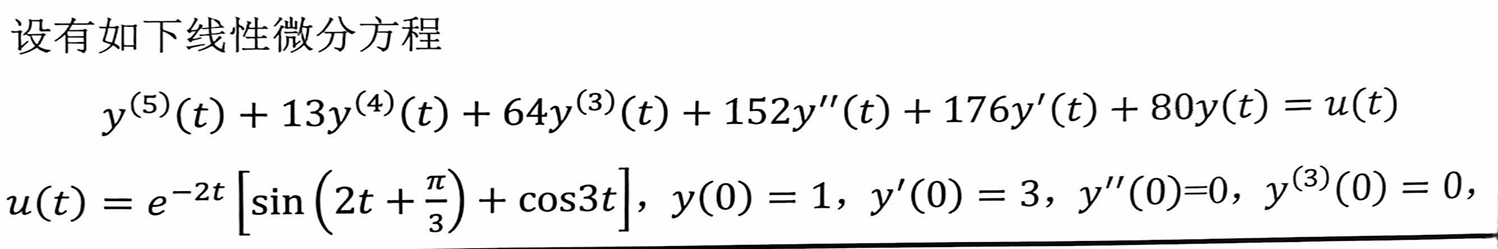
matlab 复制代码

% 读取仿真输出（此时工作区已生成OUTY）
y_data = OUTY.signals(1).values;  % 提取y(t)的数值
max_y = max(y_data);
disp(['y(t)的最大值为：', num2str(max_y)]);

要解决这个问题，我们分**Simulink模型搭建（第一题）、子系统创建（第二题）、反馈系统设计（第三题）**三个部分逐步实现：

一、第一题：Simulink搭建五阶微分方程模型并求解

核心思路

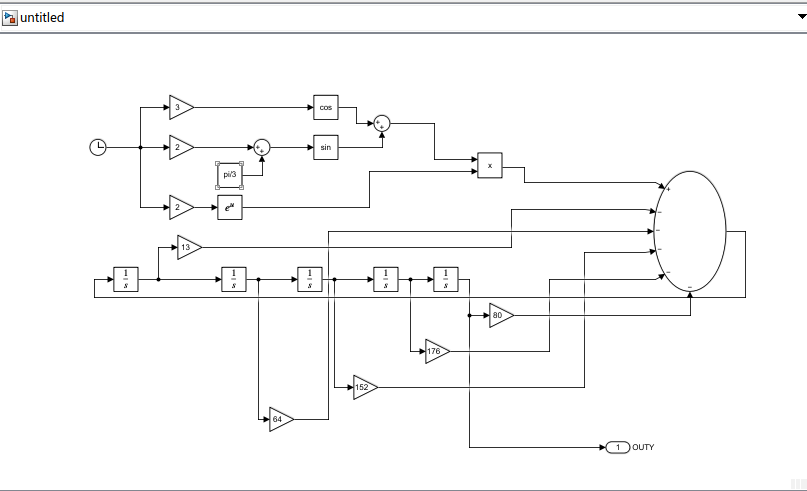
五阶微分方程需通过反向积分法 搭建：从最高阶导数 ( y^{(5)}(t) ) 出发，通过5个积分器依次得到 ( y^{(4)}(t)、y{(3)}(t)、y''(t)、y'(t)、y(t) )，再将各阶导数反馈回 ( y^{(5)}(t) ) 的计算式，同时搭建输入 ( u(t) )。

步骤1：打开Simulink并新建模型

打开MATLAB，点击主页的「Simulink」按钮，选择「Blank Model」创建空白模型。

步骤2：添加并配置模块（从Simulink库拖拽）

需添加的模块及配置如下：

模块类型	路径（Simulink Library）	数量	配置说明
Integrator	Continuous/Integrator	5	串联使用，依次积分得到 ( y^{(4)}→y{(3)}→y''→y'→y )；需设置初始条件： - 积分器1（输出 ( y^{(4)} )）：初始条件=-1（对应 ( y^{(4)}(0)=-1 )） - 积分器2（输出 ( y^{(3)} )）：初始条件=0 - 积分器3（输出 ( y'' )）：初始条件=0 - 积分器4（输出 ( y' )）：初始条件=3 - 积分器5（输出 ( y )）：初始条件=1
Sum	Signal Routing/Sum	2	① 主Sum（计算 ( y^{(5)} )）：设置「Number of inputs=6」，「Signs=±----」（对应 y(5)=u−13y(4)−64y(3)−152y′′−176y′−80yy^{(5)}=u -13y^{(4)}-64y^{(3)}-152y''-176y'-80yy(5)=u−13y(4)−64y(3)−152y′′−176y′−80y ② 辅助Sum（计算2t+π/32t+\pi/32t+π/3、sin⁡+cos⁡\sin+\cossin+cos
Gain	Math Operations/Gain	5	分别设置Gain值为13、64、152、176、80（对应各阶导数的系数）
Clock	Sources/Clock	1	输出仿真时间 ( t )
Trigonometric Function	Math Operations/Trigonometric Function	2	① 设为「sin」（输入2t+π/32t+\pi/32t+π/3）；② 设为「cos」（输入 3t3t3t）
Math Function	Math Operations/Math Function	1	设为「exp」（计算 e−2te^{-2t}e−2t）
Product	Math Operations/Product	1	计算e−2t×[sin⁡(2t+π/3)+cos⁡3t]e^{-2t} \times [\sin(2t+\pi/3)+\cos3t]e−2t×[sin(2t+π/3)+cos3t]（即 u(t)u(t)u(t)）
Outport	Sinks/Outport	1	双击设置「Signal name=OUTY」（保存 ttt 和 y(t)y(t)y(t)到工作区）

步骤3：连接模块（核心逻辑）

搭建 u(t)u(t)u(t) 信号：
- Clock → Gain（值=2）→ Sum（+）← Constant（值=π/3）→ 输出 ( 2t+\pi/3 ) → 连到「sin」模块输入；
- Clock → Gain（值=3）→ 连到「cos」模块输入；
- 「sin」和「cos」的输出 → Sum（+）→ 得到 sin⁡(2t+π/3)+cos⁡3t\sin(2t+\pi/3)+\cos3tsin(2t+π/3)+cos3t；
- Clock → Gain（值=-2）→ 「exp」模块 → 得到 e−2te^{-2t}e−2t；
- 上述两个结果 → Product模块 → 输出 u(t)u(t)u(t)。
搭建微分方程回路：
- $u(t) ) → 主Sum的第1个输入（+端）；
- 积分器1输出（y(4)y^{(4)}y(4)）→ Gain（13）→ 主Sum第2个输入（-端）；
- 积分器2输出（y(3)y^{(3)}y(3)）→ Gain（64）→ 主Sum第3个输入（-端）；
- 积分器3输出（y′′y''y′′）→ Gain（152）→ 主Sum第4个输入（-端）；
- 积分器4输出（y′y'y′）→ Gain（176）→ 主Sum第5个输入（-端）；
- 积分器5输出（yyy）→ Gain（80）→ 主Sum第6个输入（-端）；
- 主Sum输出（y(5)y^{(5)}y(5)）→ 积分器1的输入；
- 积分器5输出（y(t)y(t)y(t)）→ Outport模块。

步骤4：仿真与计算最大值

点击模型窗口「Simulation」→「Configuration Parameters」，设置「Stop time=100」；
点击「Run」运行仿真；
仿真完成后，工作区生成OUTY变量（结构体，含time和signals.values）；

在MATLAB命令行输入：

matlab 复制代码

max_y = max(OUTY.signals.values); % 计算y(t)的最大值
disp(['y(t)的最大值为：', num2str(max_y)]);

二、第二题：创建子系统SYSPPlant与SYSInput

步骤1：创建被控对象子系统SYSPPlant

在Simulink模型中，选中主Sum、5个Integrator、5个Gain （即从 ( u(t) ) 输入到 y(t)y(t)y(t)输出的回路）；
右键 → 选择「Create Subsystem」→ 命名为「SYSPPlant」（子系统自动生成1个输入端口（对应u(t)u(t)u(t)和1个输出端口（对应 y(t)y(t)y(t)）。

步骤2：创建输入子系统SYSInput

选中搭建 ( u(t) ) 的所有模块（Clock、Trigonometric、Math Function、Sum、Product）；
右键 → 选择「Create Subsystem」→ 命名为「SYSInput」（子系统输出为 ( u(t) )）。

子系统连接后的Simulink图

最终图结构：SYSInput输出 → SYSPPlant输入 → Outport（OUTY）。

三、第三题：单位负反馈系统设计（含PID校正）

步骤1：搭建单位负反馈系统

删除SYSInput，添加Step模块（Sources/Step）：设置「Final value=1」（单位阶跃输入）；
添加PID Controller模块（Continuous/PID Controller）；
添加Sum模块（Signal Routing/Sum）：设置「Signs=±」（+端接Step输入，-端接SYSPPlant输出，实现负反馈）；
连接：Step → Sum（+）← SYSPPlant输出；Sum输出 → PID Controller → SYSPPlant输入。

子问题（1）：仅P控制的临界稳定分析

双击PID Controller，设置ki=0、kd=0（仅保留比例控制 ( k_p )）；
逐步增大 ( k_p ) 并仿真，观察响应：当响应出现等幅振荡时，系统进入临界稳定（需多次调试，( k_p ) 大致在200~300区间）。

子问题（2）：PI控制的参数调整

保持 ( k_p ) 接近临界值，逐步增大 ( k_i )（积分系数）；
调整目标：响应无超调且快速收敛，最终通过仿真读取「调节时间」（输出进入稳态值±2%误差带的时间）。

关键注意事项

Integrator的初始条件必须严格匹配题目给定值，否则响应错误；
Sum模块的「Signs」设置需与微分方程的符号一致（避免符号错误导致回路发散）；
子系统创建时需确保输入/输出端口与信号流向匹配。

控制系统建模仿真（十）:实战篇——从工具掌握到工程化落地

前言

第一题：M 函数实现 for/while 循环计算

一、解题思路

二、完整代码

1. M函数文件（需保存为 fun.m，与MATLAB工作目录一致）

2. 测试代码（在MATLAB命令行或脚本中运行）

第二题：非线性约束最小优化

一、解题思路

一、问题背景：待求解的优化问题

二、完整代码

代码一：

代码二：

代码三：

三、运行结果

第三题：求解线性方程组

一、解题思路

二、完整代码

三、运行结果

第四题：响应曲线建模

一、解题思路

二、完整代码

三、运行结果

第五题：稳定性判别

一、解题思路

二、完整代码

三、运行结果

第六题：实时控制系统设计

一、第一题：Simulink搭建五阶微分方程模型并求解

核心思路

步骤1：打开Simulink并新建模型

步骤2：添加并配置模块（从Simulink库拖拽）

步骤3：连接模块（核心逻辑）

步骤4：仿真与计算最大值

二、第二题：创建子系统SYSPPlant与SYSInput

步骤1：创建被控对象子系统SYSPPlant

步骤2：创建输入子系统SYSInput

子系统连接后的Simulink图

三、第三题：单位负反馈系统设计（含PID校正）

步骤1：搭建单位负反馈系统

子问题（1）：仅P控制的临界稳定分析

子问题（2）：PI控制的参数调整

关键注意事项

1. M函数文件（需保存为 `fun.m`，与MATLAB工作目录一致）