机器学习分类
不同的学习思路对应假设空间中不同的建模⽅式与学习⽅法; 参数模型和⾮参数模型的区别体现的是全局普适性和局部适⽤性的区别; 数据模型和算法模型的区别体现的是可解释性和精确性的区别; ⽣成模型和判别模型的区别体现的是联合分布和条件分布的区别。
机器学习需要根据问题特点 和已有数据确定具有最强解释性或预测⼒的模型,其过程也可以划分为类似于"学习 - 练习 - 考试"这样的三个阶段,每个阶段的⽬标和使⽤的资源可以归纳如下**: 模型拟合(model fitting):利⽤训练数据集(training set)对模型的普通参数进⾏拟 合; 模型选择(model selection):利⽤验证数据集(validation set)对模型的超参数进⾏ 调整,筛选出性能最好的模型; 模型评价(model assessment):利⽤测试数据集(test set)来估计筛选出的模型在 未知数据上的真实性能**
设计原则
模型拟合本身只是简单的数学问题,交给 计算机就可以万事⼤吉,可模型设计 却颇有⻔道,涉及到更多的思考:⼀⽅⾯,模型的合理 性很⼤程度上取决于待解决问题本身的特征;另⼀⽅⾯,模型的复杂度也要和问题的复杂度 相匹配。在机器学习中,对这两个基本准则的理解催⽣了两个基本的规律,分别是**⽆免费午 餐定理和奥卡姆剃⼑原则**
⽆免费午餐(No Free Lunch, NFL)定理证明了任何模型在所有问题上的性能都是相 同的,其总误差和模型本身是没有关系的。NFL 定理的⼀个核⼼前提,也就是每种问题 出现的概率是均等的,每个模型⽤于解决所有问题时,其平均意义上的性能是⼀样的 。NFL 定理最重要的指导意义在于先验知识的使⽤,也就是具体问题具体分析。脱离问题的实际情况谈论模型优劣是没有意义的,只有让模型的特 点和问题的特征相匹配,模型才能发挥最⼤的作⽤。
在机器学习的场景下,奥卡姆剃⼑(Occam's Razor)可 以理解为如果有多种模型都能够同等程度地符合同⼀个问题的观测结果,那就应该选择其中 使⽤假设最少的,也就是最简单的模型。尽管越复杂的模型通常能得到越精确的结果,但是 在结果⼤致相同的情况下,模型就越简单越好。
本质上说,奥卡姆剃⼑的关注点是模型复杂度 。机器学习学到的模型应该能够识别出数据背 后的模式,也就是数据特征和数据类别之间的关系。当模型本身过于复杂时,特征和类别之 间的关系中所有的细枝末节都被捕捉,主要的趋势反⽽在乱花渐欲迷⼈眼中没有得到应有的 重视,这就会导致过拟合(overfitting )的发⽣。反过来,如果模型过于简单,它不仅没有 能⼒捕捉细微的相关性,甚⾄连主要趋势本身都没办法抓住,这样的现象就是**⽋拟合 (underfitting)**
理想的模型应该是低偏差低⽅差的双低模型
模型的复杂度越低,其偏差也就越⾼;模型的复杂度越⾼,其⽅差也就越⾼
⽆免费午餐定理说明模型的选取要以问题的特点为根据; 奥卡姆剃⼑说明在性能相同的情况下,应该选取更加简单的模型; 过于简单的模型会导致⽋拟合,过于复杂的模型会导致过拟合; 从误差分解的⻆度看,⽋拟合模型的偏差较⼤,过拟合模型的⽅差较⼤。
模型验证的作⽤是选择最佳模型并确定其性能; 对数据的重采样可以直接实现对样本外误差,也就是泛化误差的估计; 折交叉验证是⽆放回的重采样⽅法; k ⾃助采样是有放回的重采样⽅法
机器学习模型的评估
⼆分类任务是最重要也最基础的机器学习任务,其最直观的性能度量指标就是分类的准确 率。
分类正确的样本占样本总数的⽐例是精度 (accuracy),分类错误的样本占样本总数的⽐例是错误率(error rate),两者之和等于 1
机器学习采⽤了混淆矩阵(confusion matrix),也叫列联表 (contingency table)来对不同的划分结果加以区分
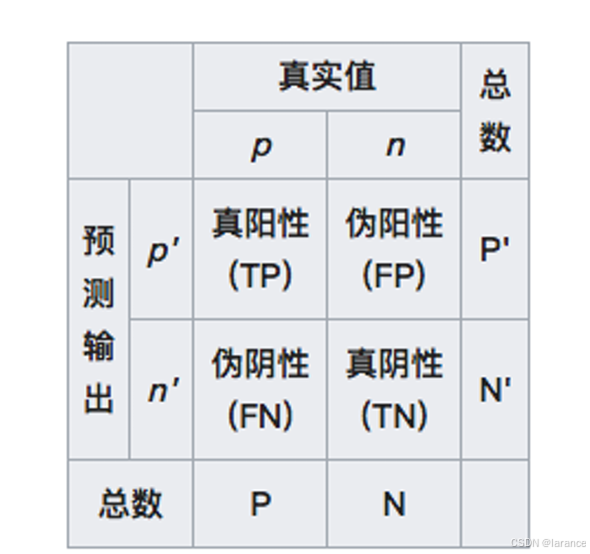
在混淆矩阵中,所有测试样例被分为真正例(true positive, TP)、假正例 (false positive, FP)、假反例(false negative, FN)、真反例(true negative, TN)四 ⼤类。
查准率 也叫正例预测值(positive predictive value),表示的是真正例占所有预测结果 为正例的样例的⽐值,也就是模型预测结果的准确程度。 查全率 也叫真正例率(true positive rate, TPR),表示的是真正例占所有真实情况为 正例的样例的⽐值,也就是模型对真实正例的判断能⼒。
将查准率和查全率画在同⼀个平⾯直⻆坐标系内,得到的就是 P-R 曲线,它表示了模型可 以同时达到的查准率和查全率。
受试者⼯作特征曲线 (receiver operating characteristic curve),简称 ROC 曲线。
ROC 曲线描述的是真正例率和假正例率之间的关系,也就是收益(真正例)与代价(假正 例)之间的关系。所谓的假正例率(false positive rate, FPR)等于假正例和所有真实反例 之间的⽐值,其数学表达式为
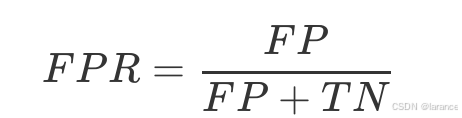
ROC 空间将 FPR 定义为 轴,TPR 定义为 轴。给定⼀个⼆元分类模型和它的阈值, 就能计算出模型的 FPR 和 TPR,并映射成由 (0, 0)、(0, 1)、(1, 0)、(1, 1) 四个点围成的正 ⽅形⾥。在这个正⽅形⾥,从 (0, 0) 到 (1, 1) 的对⻆线代表了⼀条分界线,叫作⽆识别率 线,它将 ROC 空间划分为左上/右下两个区域。
**ROC 曲线下⾯积(Area Under ROC Curve)简称 AUC。**由于 AUC 的计算是在 的⽅格⾥求⾯积,因此其取值必然在 0 到 1 之间。
在⼆分类任务中,模型性能度量的基本指标是精度和错误率,两者之和为 1; 混淆矩阵是个 的性能度量矩阵,其元素分别是真正例、假正例、假反例和真反例 的数⽬; 2×2 P-R 曲线表示的是查准率和查全率之间的关系,曲线在点 (1, 1) 上达到最优性能; ROC 曲线表示的是真正例率和假正例率之间的关系,曲线在点 (0, 1) 上达到最优性能。