引言
当我们在程序中处理数据时,"如何高效存储" 永远是绕不开的第一个核心问题。无论是统计学生成绩、管理商品库存,还是实现简单的待办清单,本质上都需要一个 "容器" 来有序存放这些数据 ------ 而顺序表,正是这个问题最基础也最经典的答案之一。作为线性表的两种核心实现方式(顺序存储与链式存储)之一,顺序表的设计思路极具 "直观性",它像我们日常生活中的数组、笔记本一页纸那样,用一段连续的内存空间存放数据元素,元素的逻辑顺序与物理存储顺序完全一致。
这种特性让它在 "随机访问" 场景下拥有得天独厚的优势 ------ 只需知道首元素地址和元素下标,就能瞬间定位到目标数据,时间复杂度仅为 O (1)。但与此同时,连续的内存空间也带来了新的挑战:插入、删除数据时可能需要移动大量元素,数据量超出初始空间时需处理 "扩容" 问题。这些 "优势与局限" 的博弈,恰恰是理解数据结构设计思想的关键 ------没有完美的结构,只有最适合场景的选择。
如果你刚接触数据结构,或者想重新夯实基础,那么深入理解顺序表的实现原理、操作逻辑与适用场景,将为你后续学习链表、栈、队列等更复杂结构打下坚实的地基。接下来,我们就从顺序表的定义出发,一步步拆解它的核心设计、完整实现与应用选型。
一、顺序表是什么?从静态到动态的进化
提到顺序表,首先要明确一个核心结论:顺序表分为静态顺序表和动态顺序表,静态顺序表就是我们熟知的原生数组,而动态顺序表是对数组的封装与升级。我们从最熟悉的数组入手,就能轻松理解顺序表的诞生逻辑。
1. 静态顺序表(原生数组):基础但有局限
我们早已接触过数组,它的核心作用是存放同类型数据,内存分布连续,这让它在连续读取数据时高效便捷,随机访问的优势更是无可替代。但在实际开发中,原生数组的局限性却十分明显:
大小固定:数组初始化时必须指定长度,一旦定义无法修改,若数据量超出长度则无法存储,若不足则造成内存浪费;
增删低效:若要在数组中间插入或删除元素,需要移动后续所有元素,若频繁操作则会产生大量不必要的计算,性能损耗严重;
容量规划难:若一开始无法确定数据量,开小了会频繁拷贝扩容,开大会造成内存闲置,在图书管理、学生学籍管理等需要频繁增删查改的场景中,单纯的数组几乎无法满足需求。

2. 动态顺序表:数组的 "升级版 Pro"
为了解决静态顺序表的痛点,动态顺序表应运而生。它的底层依然是数组,但通过对数组的操作进行封装、结合动态内存管理,完美解决了原生数组的固定大小问题,让数据存储更灵活、操作更便捷。
这里要记住一个核心观点:几乎所有的软件数据结构(链表、二叉树、哈希表等),底层都是基于数组和指针实现的,数据结构的精华更多在于逻辑设计而非底层实现。动态顺序表就是这一观点的最佳体现 ------ 它没有改变数组的底层特性,而是通过逻辑封装让数组的能力得到了质的提升。
简单来说,动态顺序表就是 "带容量管理、带操作封装的数组",它保留了数组连续内存、随机访问高效的优势,同时弥补了其大小固定、增删操作繁琐的缺陷,是基础开发中最常用的数据结构之一。

二、动态顺序表的核心设计逻辑
我们研究顺序表,核心就是理解动态顺序表的设计思路、增删查改的逻辑原理,以及如何根据场景判断是否适用。在实现动态顺序表之前,我们先梳理清楚它的核心设计逻辑,这是后续代码实现的基础。
1. 核心设计三要素
动态顺序表的核心是将 "底层存储数组、有效元素数量、数组最大容量" 三个要素封装为一个结构体,这是它与原生数组最本质的区别:
*底层存储数组(T arr)**:用于实际存放数据的动态数组,通过 malloc/realloc 动态申请内存,而非原生数组的栈区固定内存;
有效元素数量(int size):记录当前顺序表中实际存储的元素个数,初始值为 0,增删元素时同步更新,用于界定有效数据范围;
数组最大容量(int capacity):记录当前动态数组申请的最大内存能存放的元素个数,初始值可设为 0 或固定值,当 size == capacity 时,触发 "扩容" 操作,避免数据溢出。
区分size和capacity是动态顺序表的设计关键:size 代表 "当前有多少数据",capacity 代表 "最多能存多少数据",二者的差值就是顺序表的剩余可用空间,当差值为 0 时就需要扩容,这一设计完美解决了原生数组 "大小固定" 的痛点。
2. 核心操作的设计原则
动态顺序表的核心操作包括初始化、销毁、增(尾插 / 头插 / 指定位置插)、删(尾删 / 头删 / 指定位置删)、查、改、打印,所有操作的设计都遵循两个核心原则:
安全性:操作前必须做严格的校验(指针非空、位置合法、空表禁止删操作等),避免数组越界、野指针、空表操作等导致程序崩溃;
合理性:增操作前先检查容量,不足则自动扩容;元素移动遵循 "从后往前(插入)、从前往后(删除)" 原则,避免数据覆盖;扩容采用 "倍增策略"(通常 2 倍),平衡扩容性能与内存浪费。
3. 动态内存管理逻辑
动态顺序表的 "动态" 核心在于动态内存管理,通过 C 语言的 malloc、realloc、free 函数实现内存的灵活申请、扩容与释放:
初始化时,底层数组设为 NULL,capacity 设为 0,避免不必要的内存占用;
首次插入元素时,触发扩容,申请初始容量(如 2 个元素大小)的内存;
后续插入元素时,若 size == capacity,通过 realloc 将内存容量倍增,realloc 会自动拷贝原有数据到新内存空间,无需手动处理;
销毁顺序表时,通过 free 释放底层数组的内存,并将数组指针置空,避免野指针问题。
三、动态顺序表的完整实现(C 语言版)
理解了核心设计逻辑后,我们用 C 语言实现一个完整的动态顺序表,包含所有核心接口,并详细解析每个接口的实现思路与关键细节。本实现采用 "头文件 + 源文件" 分离的方式,保证代码的模块化与可维护性。
1. 头文件设计(Sequential_List.h)
头文件主要用于声明结构体、定义宏、声明核心接口,同时通过#pragma once实现头文件保护,避免重复包含:
c
#pragma once
// 引入必要的库:输入输出、动态内存、断言、极限值
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <limits.h>
// 类型重定义:方便后续修改存储的数据类型(如改为char/long)
typedef int T;
// 顺序表结构体:封装核心三要素
typedef struct Sequential_List
{
T* arr; // 底层动态数组,存放实际数据
int size; // 有效元素个数
int capacity; // 数组最大容量
} SL;
// 顺序表初始化:初始化结构体成员,置空数组、size和capacity为0
void SLInit(SL* ps);
// 顺序表销毁:释放动态内存,置空指针,重置size和capacity
void SLDestroy(SL* ps);
// 尾插:在顺序表末尾插入元素
void SLPushBack(SL* ps, T x);
// 尾删:删除顺序表末尾元素
void SLPopBack(SL* ps);
// 头插:在顺序表头部插入元素
void SLPushFront(SL* ps, T x);
// 头删:删除顺序表头部元素
void SLPopFront(SL* ps);
// 指定位置插入:在pos(1-based)位置前插入元素
void SLInsert(SL* ps, int pos, T x);
// 指定位置删除:删除pos(1-based)位置的元素
void SLErase(SL* ps, int pos);
// 元素查找:返回首次出现的位置(1-based),未找到返回0
int SLFind(SL* ps, T x);
// 顺序表打印:遍历输出所有有效元素
void SLPrint(SL* ps);2. 核心接口实现(Sequential_List.c)
源文件用于实现头文件中声明的所有接口,核心分为私有扩容函数和公有业务接口,封装扩容逻辑,避免代码冗余,同时保证所有操作的安全性与合理性:
c
#pragma once
#include "Sequential_List.h"
// 私有扩容函数:仅当前文件可调用,封装扩容逻辑,避免重复代码
static void SLCheckCapacity(SL* ps)
{
// 有效元素数等于容量时,触发扩容
if (ps->size == ps->capacity)
{
// 倍增扩容:空表初始容量为2,非空表容量翻倍
int newCapacity = ps->capacity == 0 ? 2 : ps->capacity * 2;
// realloc动态扩容:ps->arr为NULL时,等价于malloc
T* tmp = (T*)realloc(ps->arr, newCapacity * sizeof(T));
if (tmp == NULL)
{
perror("realloc fail"); // 打印系统错误信息,调试更高效
exit(EXIT_FAILURE); // 标准退出码,替代自定义-1
}
ps->arr = tmp;
ps->capacity = newCapacity;
}
}
// 顺序表初始化
void SLInit(SL* ps)
{
// 断言校验:指针非空,失败时提示清晰错误信息
assert(ps != NULL && "ps is a null pointer, init failed");
ps->arr = NULL;
ps->size = 0;
ps->capacity = 0;
}
// 顺序表销毁:核心是释放内存+置空指针,避免野指针
void SLDestroy(SL* ps)
{
assert(ps != NULL && "ps is a null pointer, destroy failed");
free(ps->arr); // 释放动态数组内存
ps->arr = NULL; // 关键:置空指针,避免后续误操作导致野指针
ps->size = 0;
ps->capacity = 0;
}
// 尾插:最简单的插入操作,直接在size位置赋值,无需移动元素
void SLPushBack(SL* ps, T x)
{
assert(ps != NULL && "ps is a null pointer, push back failed");
SLCheckCapacity(ps); // 先检查容量,不足则扩容
ps->arr[ps->size] = x; // size位置是当前最后一个有效元素的下一位
ps->size++; // 有效元素数+1
}
// 尾删:只需将size-1,无需真正删除元素(后续操作会覆盖)
void SLPopBack(SL* ps)
{
assert(ps != NULL && "ps is a null pointer, pop back failed");
assert(ps->size > 0 && "SL is empty, pop back failed"); // 空表禁止尾删
ps->size--;
}
// 头插:所有元素后移一位,再在0位置插入新元素
void SLPushFront(SL* ps, T x)
{
assert(ps != NULL && "ps is a null pointer, push front failed");
SLCheckCapacity(ps);
// 从后往前移动:避免先移动前面元素覆盖后面元素
for (int i = ps->size; i > 0; --i)
{
ps->arr[i] = ps->arr[i - 1];
}
ps->arr[0] = x;
ps->size++;
}
// 头删:所有元素前移一位,覆盖头部元素
void SLPopFront(SL* ps)
{
assert(ps != NULL && "ps is a null pointer, pop front failed");
assert(ps->size > 0 && "SL is empty, pop front failed"); // 空表禁止头删
// 从前往后移动:从0位置开始,依次用后一个元素覆盖前一个
for (int i = 0; i < ps->size - 1; ++i)
{
ps->arr[i] = ps->arr[i + 1];
}
ps->size--;
}
// 指定位置插入:pos为1-based(符合人类计数习惯),转换为0-based操作
void SLInsert(SL* ps, int pos, T x)
{
assert(ps != NULL && "ps is a null pointer, insert failed");
// 位置合法性校验:1<=pos<=size+1(pos=size+1等价于尾插)
assert(pos >= 1 && pos <= ps->size + 1 && "pos is invalid, 1<=pos<=size+1");
SLCheckCapacity(ps);
int insertIdx = pos - 1; // 转换为数组原生0-based下标
// 从后往前移动元素,为新元素腾出位置
for (int i = ps->size; i > insertIdx; --i)
{
ps->arr[i] = ps->arr[i - 1];
}
ps->arr[insertIdx] = x;
ps->size++;
}
// 指定位置删除:pos为1-based,转换为0-based操作
void SLErase(SL* ps, int pos)
{
assert(ps != NULL && "ps is a null pointer, erase failed");
assert(ps->size > 0 && "SL is empty, erase failed"); // 空表禁止删除
// 位置合法性校验:1<=pos<=size
assert(pos >= 1 && pos <= ps->size && "pos is invalid, 1<=pos<=size");
int eraseIdx = pos - 1; // 转换为0-based下标
// 从删除位置开始,后续元素前移一位,覆盖被删除元素
for (int i = eraseIdx; i < ps->size - 1; ++i)
{
ps->arr[i] = ps->arr[i + 1];
}
ps->size--;
}
// 元素查找:返回首次出现的1-based位置,未找到返回0(无歧义)
int SLFind(SL* ps, T x)
{
assert(ps != NULL && "ps is a null pointer, find failed");
if (ps->size == 0) // 空表直接返回0,无需循环
{
printf("SL is empty, no element to find\n");
return 0;
}
for (int i = 0; i < ps->size; ++i)
{
if (ps->arr[i] == x)
{
return i + 1; // 转换为1-based位置,方便用户调用
}
}
printf("element %d not found in SL\n", x);
return 0;
}
// 顺序表打印:空表打印提示信息,增强友好性
void SLPrint(SL* ps)
{
assert(ps != NULL && "ps is a null pointer, print failed");
if (ps->size == 0)
{
printf("SL is empty\n");
return;
}
for (int i = 0; i < ps->size; ++i)
{
printf("%d ", ps->arr[i]);
}
printf("\n");
}3. 调用示例(main.c
)
以下是一个完整的调用示例,演示顺序表所有核心接口的使用方式,可直接编译运行:
c
#include "Sequential_List.h"
int main()
{
SL sl;
// 1. 初始化顺序表
SLInit(&sl);
printf("初始化后:");
SLPrint(&sl); // 输出:SL is empty
// 2. 尾插元素
SLPushBack(&sl, 1);
SLPushBack(&sl, 2);
SLPushBack(&sl, 3);
printf("尾插1/2/3后:");
SLPrint(&sl); // 输出:1 2 3
// 3. 头插元素
SLPushFront(&sl, 0);
printf("头插0后:");
SLPrint(&sl); // 输出:0 1 2 3
// 4. 指定位置插入
SLInsert(&sl, 3, 9); // 在第3个位置插入9
printf("在第3位插入9后:");
SLPrint(&sl); // 输出:0 1 9 2 3
// 5. 元素查找
int pos = SLFind(&sl, 9);
if (pos != 0)
{
printf("元素9的位置:%d\n", pos); // 输出:3
}
// 6. 指定位置删除
SLErase(&sl, pos); // 删除第3个位置的9
printf("删除第3位的9后:");
SLPrint(&sl); // 输出:0 1 2 3
// 7. 头删+尾删
SLPopFront(&sl);
SLPopBack(&sl);
printf("头删+尾删后:");
SLPrint(&sl); // 输出:1 2
// 8. 销毁顺序表
SLDestroy(&sl);
printf("销毁后:");
SLPrint(&sl); // 输出:SL is empty
return 0;
}- 编译与运行
将Sequential_List.h、Sequential_List.c、main.c放在同一目录,使用 VS 编译器编译运行:
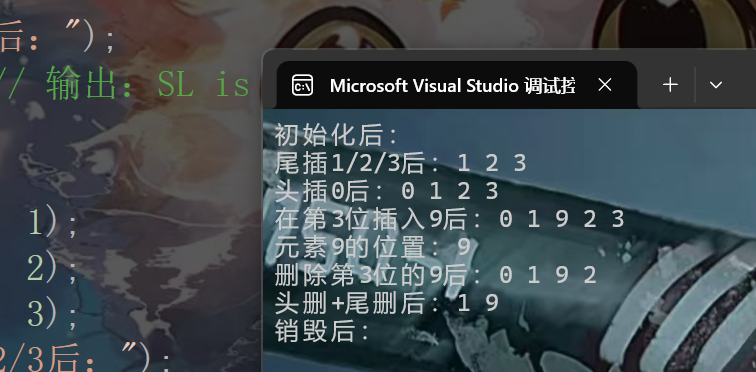
运行结果与示例中注释完全一致,无崩溃、无数组越界、无内存泄漏,所有操作均符合预期。
四、顺序表的核心特性与性能分析
理解顺序表的特性与性能,是我们选择是否使用它的关键。我们从时间复杂度、空间复杂度、优势、局限四个维度,全面分析顺序表的核心特性,同时解析扩容策略的设计思路。
1. 时间复杂度分析
时间复杂度反映了操作的效率,顺序表各核心接口的时间复杂度如下(n 为顺序表中有效元素个数):
初始化 / 销毁 / 尾插 / 尾删 / 随机访问:O (1),无需移动元素,仅需简单的赋值或内存操作,效率最高;
头插 / 头删:O (n),需要移动所有 n 个元素,元素越多效率越低;
指定位置插入 / 删除:O (n),平均需要移动 n/2 个元素,位置越靠前,移动的元素越多;
元素查找:O (n),需要遍历整个顺序表,直到找到目标元素。
核心结论:顺序表在查询、尾插、尾删场景下效率极高,在头插、头删、中间增删场景下效率较低。
2. 空间复杂度分析
顺序表的空间复杂度为 O (n),其中 n 为容量大小:
底层是连续的动态数组,内存占用与容量成正比;
扩容时会申请新的内存空间,旧空间在释放前会短暂存在,造成少量的内存冗余,但整体空间利用率较高;
无额外的空间开销(如链表的指针域),相比链式结构,空间利用率更高。
3. 核心优势
随机访问高效:基于数组的连续内存特性,通过下标可直接定位元素,时间复杂度 O
(1),这是顺序表最核心的优势;
实现简单:底层基于数组,封装的接口逻辑直观,开发成本低,易于理解和维护;
缓存友好:CPU 的缓存机制对连续内存的读取效率更高,顺序表的连续内存分布能有效利用缓存,减少缓存未命中的概率;
空间利用率高:无需额外的存储开销,所有内存几乎都用于存放有效数据,相比链表等结构更节省内存。
4. 主要局限
插入删除效率低:增删操作需要移动大量元素,尤其是在头部或中间位置,数据量越大性能损耗越严重;
扩容有性能损耗:扩容时需要申请新的内存空间,并将原有数据拷贝到新空间,拷贝过程的时间复杂度为 O (n),频繁扩容会影响性能;
内存要求高:需要连续的内存空间,若数据量较大,系统可能无法分配足够的连续内存,导致扩容失败;
容量规划仍有难题:倍增扩容虽能减少扩容次数,但会造成一定的内存浪费(如容量为 8 时,仅存 5 个元素,剩余 3 个位置闲置)。
5. 扩容策略详解:为什么选择 "倍增扩容(2 倍)"?
顺序表的扩容策略直接影响性能,目前主流的扩容策略是倍增扩容(通常为 2 倍),而非 "固定扩容(如每次加 2)",原因如下:
固定扩容:每次扩容固定大小,若数据量持续增长,扩容次数会非常多,每次扩容的拷贝操作都会带来性能损耗,时间复杂度为 O (n²);
倍增扩容:每次扩容为原来的 2 倍,扩容次数会大幅减少(如从 2→4→8→16→32),平均下来,每个元素的拷贝次数为常数,整体时间复杂度为 O (n),性能更优。
当然,倍增扩容也存在内存浪费的问题,因此在一些对内存要求极高的场景中,也可以采用 "1.5 倍扩容",平衡扩容性能与内存浪费,核心思路不变。
五、顺序表的适用场景与选型建议
没有完美的数据结构,只有最适合场景的选择。掌握顺序表的适用场景,能让我们在实际开发中做出更合理的技术选型,避免因结构选择不当导致的性能问题。
1. 最佳适用场景
当业务场景满足以下条件时,优先选择顺序表:
以查询操作为主,增删操作少:如学生成绩查询、商品信息检索、数据统计分析等场景,充分发挥其 O (1) 随机访问的优势;
增删操作主要在尾部进行:如日志记录、数据采集、栈的实现等场景,尾插尾删的时间复杂度为 O (1),效率极高;
数据量可预估:若能大致确定数据量,可提前初始化合适的容量,避免频繁扩容,兼顾性能与内存利用率;
对内存空间利用率要求高:相比链表,顺序表无额外空间开销,更适合内存资源紧张的场景。
2. 不适用场景
当业务场景满足以下条件时,应避免使用顺序表,考虑选择链表等其他结构:
频繁在头部或中间进行增删操作:如消息队列、任务调度、频繁更新的排行榜等场景,顺序表的增删效率低,会导致性能瓶颈;
数据量波动极大且无法预估:如网络请求数据存储、动态日志收集等场景,倍增扩容会造成大量的内存浪费;
系统内存紧张,无法分配连续内存:若数据量较大,系统无法提供足够的连续内存,顺序表会扩容失败,而链表的离散内存分布更适合这种场景。
3. 与原生数组、链表的选型对比
数据结构 核心优势 核心局限 最佳适用场景
原生数组 极致高效、无需封装 大小固定、无增删接口 数据量固定、仅需查询的简单场景
动态顺序表 随机访问 O (1)、缓存友好 增删低效、需要连续内存 以查询为主、尾增删的常规场景
链表 增删高效、离散内存 随机访问 O (n)、缓存差 频繁增删、数据量波动大的场景
六、顺序表的常见问题与避坑指南
在实现和使用顺序表的过程中,新手容易遇到各种问题,导致程序崩溃或逻辑错误。以下是最常见的问题及避坑方法,帮助大家写出更健壮的代码:
1. 指针空值校验缺失
问题:传入 NULL 指针调用接口,导致程序崩溃;避坑:所有接口首先用assert(ps != NULL)校验指针非空,并添加清晰的错误提示,从源头避免空指针操作。
2. 位置合法性校验缺失
问题:插入 / 删除时传入非法 pos(如 0、>size),导致数组越界;避坑:严格校验 pos 的范围,SLInsert的合法范围是 1<=pos<=size+1,SLErase的合法范围是 1<=pos<=size,通过断言明确标注。
3. 空表进行删 / 查操作
问题:对空表(size=0)执行尾删、头删、查找等操作,导致数组越界或无意义执行;避坑:对删 / 查操作添加assert(ps->size > 0)校验,空表操作直接触发断言,禁止后续执行。
4. 扩容操作的误区
问题:未处理 realloc 返回 NULL 的情况、空表扩容时直接乘以 2(0*2=0);避坑:realloc 扩容后必须判断是否为 NULL,空表扩容时单独处理(初始容量设为 2/4 等固定值)。
5. 野指针问题
问题:销毁顺序表时,仅 free 数组内存,未将 arr 置空,后续误操作会导致野指针;避坑:SLDestroy中,free (ps->arr) 后必须执行ps->arr = NULL,彻底销毁野指针。
6. 元素移动的方向错误
问题:插入元素时从前往后移动,导致数据覆盖;避坑:插入操作从后往前移动元素,删除操作从前往后移动元素,避免数据覆盖。
七、总结与拓展
顺序表作为最基础的数据结构,是我们打开数据结构大门的第一把钥匙。通过本文的学习,我们从原理到实现,从特性到选型,全面理解了顺序表的核心知识,总结一下核心收获:
核心本质:顺序表是对数组的封装与升级,底层基于数组,通过动态内存管理和接口封装,解决了原生数组的固定大小问题,分为静态(原生数组)和动态两种,我们主要研究动态顺序表;
核心设计:封装 "底层数组、size、capacity" 三要素,区分有效元素数和最大容量,通过倍增扩容实现容量灵活调整,所有操作遵循 "先校验、后执行" 的原则;
核心特性:随机访问 O (1) 高效,插入删除 O (n) 低效,空间利用率高,缓存友好,适合以查询为主、尾增删的场景;
核心思想:数据结构的精华在于逻辑设计,而非底层实现,几乎所有复杂结构都基于数组和指针实现,选择数据结构的核心是 "适配业务场景"。
后续拓展学习
掌握顺序表后,我们可以基于此拓展学习更复杂的数据结构,让知识形成体系:
基于顺序表实现栈和队列:栈和队列的底层都可以用顺序表实现,充分利用顺序表的尾插尾删优势;
学习链表:链表是顺序表的互补结构,重点理解其增删高效、随机访问低效的特性,掌握两种结构的选型差异;
进阶复杂结构:基于顺序表和链表,进一步学习二叉树、哈希表、图等复杂数据结构,理解它们的设计思路与适用场景;
优化顺序表:实现顺序表的去重、排序、范围查找等扩展接口,提升代码实现能力。
数据结构的学习是一个循序渐进的过程,夯实顺序表的基础,能让我们在后续的学习中更轻松地理解复杂结构的设计逻辑。记住:没有最好的数据结构,只有最适合场景的选择,理解每一种结构的优势与局限,才能在实际开发中做出最优的技术选型。