lerobot_train中scheduler具体实现

对于pi05，它的scheduler实现如下，

py 复制代码

@LRSchedulerConfig.register_subclass("cosine_decay_with_warmup")
@dataclass
class CosineDecayWithWarmupSchedulerConfig(LRSchedulerConfig):
    """Used by Physical Intelligence to train Pi0.

    Automatically scales warmup and decay steps if num_training_steps < num_decay_steps.
    This ensures the learning rate schedule completes properly even with shorter training runs.
    """

    num_warmup_steps: int
    num_decay_steps: int
    peak_lr: float
    decay_lr: float

    def build(self, optimizer: Optimizer, num_training_steps: int) -> LambdaLR:
        # Auto-scale scheduler parameters if training steps are shorter than configured decay steps
        actual_warmup_steps = self.num_warmup_steps
        actual_decay_steps = self.num_decay_steps

        if num_training_steps < self.num_decay_steps:
            # Calculate scaling factor to fit the schedule into the available training steps
            scale_factor = num_training_steps / self.num_decay_steps
            actual_warmup_steps = int(self.num_warmup_steps * scale_factor)
            actual_decay_steps = num_training_steps

            logging.info(
                f"Auto-scaling LR scheduler: "
                f"num_training_steps ({num_training_steps}) < num_decay_steps ({self.num_decay_steps}). "
                f"Scaling warmup: {self.num_warmup_steps} → {actual_warmup_steps}, "
                f"decay: {self.num_decay_steps} → {actual_decay_steps} "
                f"(scale factor: {scale_factor:.3f})"
            )

        def lr_lambda(current_step):
            def linear_warmup_schedule(current_step):
                if current_step <= 0:
                    return 1 / (actual_warmup_steps + 1)
                frac = 1 - current_step / actual_warmup_steps
                return (1 / (actual_warmup_steps + 1) - 1) * frac + 1

            def cosine_decay_schedule(current_step):
                step = min(current_step, actual_decay_steps)
                cosine_decay = 0.5 * (1 + math.cos(math.pi * step / actual_decay_steps))
                alpha = self.decay_lr / self.peak_lr
                decayed = (1 - alpha) * cosine_decay + alpha
                return decayed

            if current_step < actual_warmup_steps:
                return linear_warmup_schedule(current_step)

            return cosine_decay_schedule(current_step)

        return LambdaLR(optimizer, lr_lambda, -1)

学习率分段函数

设 ttt 为当前训练步数，给定参数：
p=2.5×10−5p = 2.5 \times 10^{-5}p=2.5×10−5（peak_lr）
d=2.5×10−6d = 2.5 \times 10^{-6}d=2.5×10−6（decay_lr）
W=1000W = 1000W=1000（warmup_steps）
D=30000D = 30000D=30000（decay_steps）
α=dp=0.1\alpha = \frac{d}{p} = 0.1α=pd=0.1

完整分段函数，
lr(t)={p⋅1+tW+10≤t<Wp⋅[(1−α)⋅1+cos⁡(πtD)2+α]W≤t≤Ddt>D \text{lr}(t) = \begin{cases} \displaystyle p \cdot \frac{1 + t}{W + 1} & 0 \leq t < W \\[12pt] \displaystyle p \cdot \left[ (1 - \alpha) \cdot \frac{1 + \cos\left(\frac{\pi t}{D}\right)}{2} + \alpha \right] & W \leq t \leq D \\[12pt] d & t > D \end{cases} lr(t)=⎩ ⎨ ⎧p⋅W+11+tp⋅[(1−α)⋅21+cos(Dπt)+α]d0≤t<WW≤t≤Dt>D

代入具体数值，
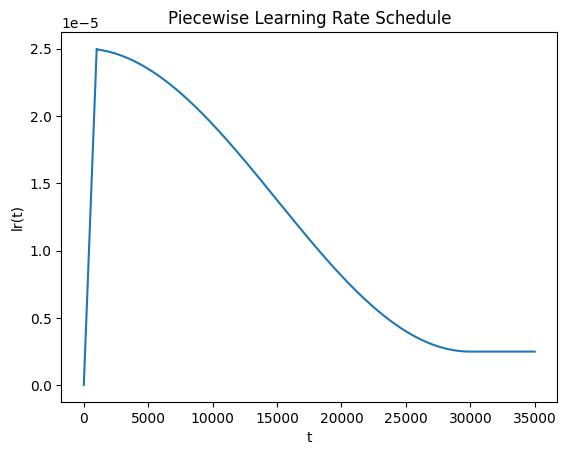
lr(t)={2.5×10−5⋅1+t10010≤t<10001.125×10−5⋅(1+cos⁡πt30000)+2.5×10−61000≤t≤300002.5×10−6t>30000 \text{lr}(t) = \begin{cases} \displaystyle 2.5 \times 10^{-5} \cdot \frac{1 + t}{1001} & 0 \leq t < 1000 \\[12pt] \displaystyle 1.125 \times 10^{-5} \cdot \left(1 + \cos\frac{\pi t}{30000}\right) + 2.5 \times 10^{-6} & 1000 \leq t \leq 30000 \\[12pt] 2.5 \times 10^{-6} & t > 30000 \end{cases} lr(t)=⎩ ⎨ ⎧2.5×10−5⋅10011+t1.125×10−5⋅(1+cos30000πt)+2.5×10−62.5×10−60≤t<10001000≤t≤30000t>30000

曲线表示为，