人工势场与领航跟随的Matlab仿真

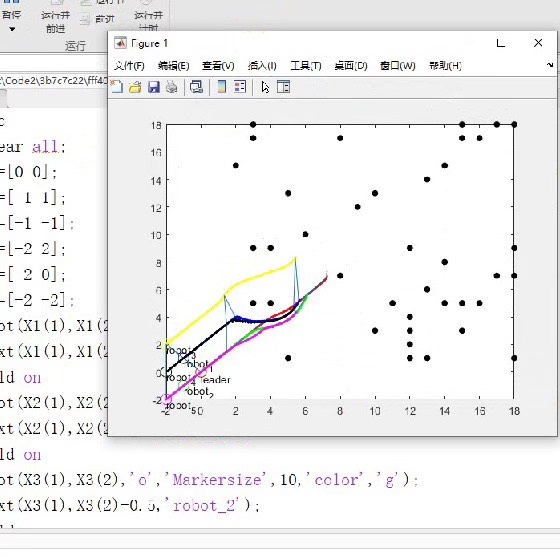
人工势场+领航跟随matlab仿真。

人工势场法这玩意儿玩路径规划确实挺有意思的，尤其是配上领航跟随策略，整个多机器人系统动起来那叫一个丝滑。今天咱们就撸起袖子整一个简单版的Matlab仿真，顺便聊聊代码里那些容易踩坑的地方。

先说说核心思想吧：领航机器人根据目标点生成引力，障碍物产生斥力，跟随机器人不仅要避开障碍，还得保持和领航者的相对位置。这里头最要命的就是势场函数的计算，咱们直接上代码：

matlab 复制代码

function [F_att, F_rep] = potential_field(q, goal, obstacles)
    % 引力参数
    K_att = 0.5;
    % 斥力参数
    K_rep = 30;
    rho_0 = 2;
    
    % 引力计算
    d_goal = norm(q - goal);
    F_att = -K_att * (q - goal);
    
    % 斥力计算
    F_rep = [0, 0];
    for i = 1:size(obstacles,1)
        d_obs = norm(q - obstacles(i,:));
        if d_obs < rho_0
            rep_dir = (q - obstacles(i,:))/d_obs;
            F_rep = F_rep + K_rep*(1/d_obs - 1/rho_0)*(1/d_obs^2)*rep_dir;
        end
    end
end

注意看斥力计算那块，K_rep调大了容易震荡，调小了又避不开障碍。有个骚操作是在机器人接近目标时减小斥力系数，这样可以避免在目标点附近震荡。不过咱们这个demo先保持简单。

人工势场+领航跟随matlab仿真。

领航者的运动控制更简单粗暴，直接朝着目标点冲：

matlab 复制代码

% 领航者运动模型
function q_leader = move_leader(q, goal, step)
    direction = (goal - q)/norm(goal - q);
    q_leader = q + direction * step;
end

跟随者的控制才是重头戏。既要考虑领航者的相对位置，又要处理势场合力。这里用了个PID保持队形：

matlab 复制代码

% 跟随者控制
error_prev = [0 0];
integral = [0 0];

function u = follower_control(q_follow, q_leader, obstacles)
    global error_prev integral
    
    % 期望相对位置
    desired_pos = q_leader - [3, 0];
    
    % PID参数
    Kp = 0.8;
    Ki = 0.01;
    Kd = 0.3;
    
    error = desired_pos - q_follow;
    integral = integral + error;
    derivative = error - error_prev;
    
    % 势场合力
    [~, F_rep] = potential_field(q_follow, desired_pos, obstacles);
    
    u = Kp*error + Ki*integral + Kd*derivative + 0.2*F_rep;
    error_prev = error;
end

注意那个0.2的系数，这是在PID输出和斥力之间找平衡。实测中发现纯势场容易让跟随者走蛇形，加上PID的微分项能有效抑制震荡。但积分项别给太大，不然超调能让你怀疑人生。

跑仿真的时候最常见的坑就是局部极小值。比如遇到凹形障碍，机器人直接卡住不动了。这时候可以加个随机扰动或者换个势场函数。不过咱们这个二维仿真里，只要把障碍物摆得不是太变态，基本都能绕过去。

最后看看效果：领航者带着三个小弟穿越障碍林，路径虽然不够最优，但好歹能安全到达。想要更丝滑的移动，可以把步长调小，代价是计算量增加。其实这个框架还能玩出很多花样，比如动态领航者、可变队形，甚至加上通信延迟模拟，那又是另一个层面的快乐（和掉头发）了。