【人工智能学习-AI入试相关题目练习-第十二次】

人工智能学习-AI入试相关题目练习-第十二次

1-前言
3-问题题目训练
問1（幅優先探索：BFS）
- 题目在问什么？
- 过程（关键步骤）
- [✅ 問1答案](#✅ 問1答案)
問2（ベイズ：条件付き概率）
- 题目在问什么？
- 关键公式（贝叶斯）
- [✅ 問2答案](#✅ 問2答案)
[問3（空栏填空：K-means / Bellman / 最急降下）](#問3（空栏填空：K-means / Bellman / 最急降下）)
- 题目在问什么？
- [① K-means](#① K-means)
- [② ベルマン方程式（强化学习）](#② ベルマン方程式（强化学习）)
- [③ 最急降下法（梯度下降）](#③ 最急降下法（梯度下降）)
- [✅ 問3总答案汇总](#✅ 問3总答案汇总)
【模擬問題①】（既出系：強化学習・MDP）
- 問題1
【模擬問題②】（既出系：教師あり学習・最適化）
- 問題2
【予測問題①】（新傾向：不確実性・確率推論）
- 問題3
【予測問題②】（新傾向：汎化・モデルの限界）
- 問題4
4-练习（日语版本）解析
【模擬問題①】問題1（強化学習・MDP）
【模擬問題②】問題2（教師あり学習・最適化）
【予測問題①】問題3（確率的推論・不確実性）
【予測問題②】問題4（汎化性能・学習限界）
- [✅ 一页速记版（考前用）](#✅ 一页速记版（考前用）)
5-単語练习（日语版本）
6-总结

1-前言

为了应对大学院考试，我们来学习相关人工智能相关知识，并做各种练习。

通过学习，也算是做笔记，让自己更理解些。

3-问题题目训练

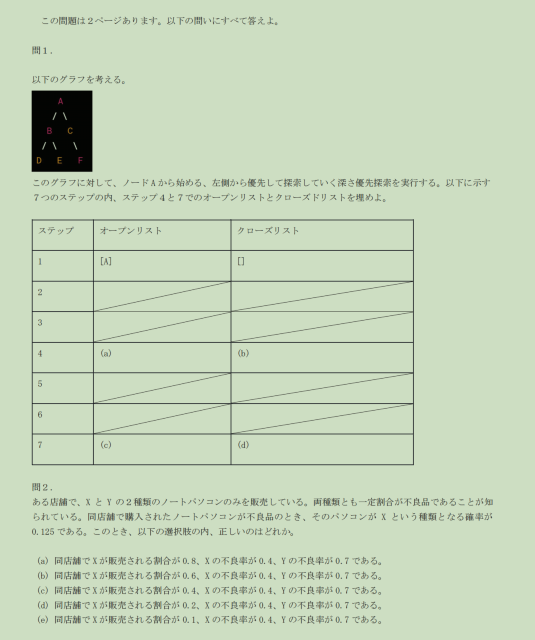
問1（幅優先探索：BFS）

题目在问什么？

从 ノードA 出发，按从左到右 做 幅優先探索（BFS） 。

题目要你填表里 ステップ4 和 ステップ7 时的：

オープンリスト（Open list）：接下来"排队等着被展开"的节点
クローズドリスト（Closed list）：已经"取出来展开过"的节点

图结构（按图）是：

A 的子：B, C
B 的子：D, E
C 的子：F

BFS 的规则就是：先进先出（队列） ，并且展开子节点时左→右入队。

过程（关键步骤）

Step1：Open= $A$ , Close=\[\]
Step2：取出A → 入Close；把B,C入Open
Open= $B,C$ , Close= $A$
Step3：取出B → 入Close；把D,E入Open
Open= $C,D,E$ , Close= $A,B$
Step4：取出C → 入Close；把F入Open
→ 就得到题目要填的 (a)(b)

之后继续：

Step5：取出D → Close= $A,B,C,D$ , Open= $E,F$
Step6：取出E → Close= $A,B,C,D,E$ , Open= $F$
Step7：取出F → Close= $A,B,C,D,E,F$ , Open=\[\]
→ 就得到题目要填的 ©(d)

✅ 問1答案

ステップ4

(a) オープンリスト：[D, E, F]
(b) クローズドリスト：[A, B, C]

ステップ7

© オープンリスト：[]
(d) クローズドリスト：[A, B, C, D, E, F]

問2（ベイズ：条件付き概率）

题目在问什么？

已知店里只卖两类电脑 X / Y ，两者都有不良率。

当你买到的是不良品 时，它属于 X 的概率是：

P(X \\mid 不良)=0.125

题目给了 5 个选项，每个选项给：

(P(X))（X 的销售比例）
(P(不良\mid X)=0.4)
(P(不良\mid Y)=0.7)

要你选哪一组数据能让 (P(X \mid 不良)=0.125)。

关键公式（贝叶斯）

P(X\\mid 不良)=\\frac{P(不良\\mid X)P(X)} {P(不良\\mid X)P(X)+P(不良\\mid Y)P(Y)}

其中 (P(Y)=1-P(X))

代入题目固定值：

0.125=\\frac{0.4p}{0.4p+0.7(1-p)}

解得：

p=0.2

✅ 問2答案

正确选项是：(d)

(P(X)=0.2)
(P(不良\mid X)=0.4)
(P(不良\mid Y)=0.7)

（也就是"卖 X 的比例是 0.2"那一项）

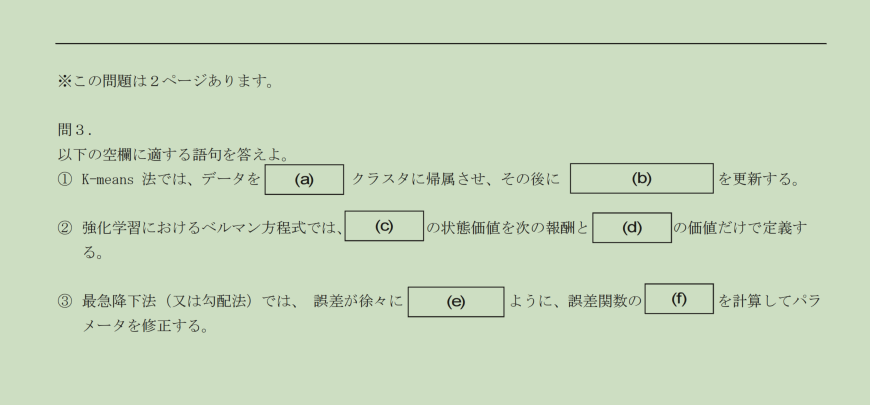
問3（空栏填空：K-means / Bellman / 最急降下）

题目在问什么？

这题就是考你是不是知道三个经典概念的标准表述，属于立命馆常见"术语挖空"。

① K-means

题干：

K-means 法では，データを (a) クラスタに帰属させ，その後に (b) を更新する。

意思（中文）：

K-means 先把每个数据分到最近的 簇，然后更新簇中心。

✅ 答案：

(a) 最近傍の（最も近い）
中文：最近的 / 最近邻的
(b) クラスタ中心（重心）
中文：簇中心（质心）

② ベルマン方程式（强化学习）

题干：

ベルマン方程式では，© の状態価値を次の報酬と (d) の価値だけで定義する。

意思（中文）：

"当前状态"的价值，可以用"下一步的奖励 + 下一状态的价值"来定义（递归）。

✅ 答案：

© 現在
中文：当前
(d) 次状態
中文：下一状态

③ 最急降下法（梯度下降）

题干：

誤差が徐々に (e) ように，誤差関数の (f) を計算してパラメータを修正する。

意思（中文）：

为了让误差逐渐变小，计算误差函数的梯度来更新参数。

✅ 答案：

(e) 小さくなる
中文：变小
(f) 勾配
中文：梯度

✅ 問3总答案汇总

(a) 最近傍の（最も近い）
(b) クラスタ中心（重心）
© 現在
(d) 次状態
(e) 小さくなる
(f) 勾配

【模擬問題①】（既出系：強化学習・MDP）

問題1

強化学習では，エージェントが環境との相互作用を通じて学習を行う。

このとき，状態遷移が現在の状態と行動のみに依存するという性質を (a) という。

この仮定に基づき，強化学習の問題は (b) として定式化される。

(b) は，状態集合，行動集合，遷移確率，および © から構成される。

価値関数に基づく手法では，将来得られる報酬を現在の価値として評価するため，

報酬は (d) によって重み付けされる。

このとき，最適価値関数は (e) によって再帰的に定義され，

この関係式を (f) 方程式と呼ぶ。

(a)～(f) に入る最も適切な語句を記せ。

【模擬問題②】（既出系：教師あり学習・最適化）

問題2

教師あり学習では，入力データとそれに対応する (a) の組を用いて学習を行う。

モデルの学習は，一般に (b) を最小化する最適化問題として定式化される。

この最適化において，パラメータの更新方向を決定するために © が計算され，

更新量は (d) によって調整される。

勾配に基づく最適化手法では，誤差関数の形状によっては

局所的な最小値である (e) に収束する可能性がある。

この問題を緩和するため，(f) を導入することで

学習の安定性を向上させる手法が用いられる。

(a)～(f) に入る語句を記せ。

【予測問題①】（新傾向：不確実性・確率推論）

問題3

知能システムが実環境で動作する場合，観測情報にはしばしば (a) が含まれる。

そのため，状態を一意に決定することが困難となる。

このような状況では，状態を (b) として表現し，

観測が得られるたびにその分布を更新する手法が用いられる。

前者では (d) に基づいて状態分布を更新する。

後者では，観測モデルを用いて (e) を計算し，

分布の総和が 1 となるように (f) が行われる。

(a)～(f) に入る最も適切な語句を記せ。

【予測問題②】（新傾向：汎化・モデルの限界）

問題4

機械学習モデルは，学習データに対して高い性能を示しても，

未知データに対して同様の性能を示すとは限らない。

このような現象は，モデルが学習データに過度に適合することによって生じ，

一般に (a) と呼ばれる。

(a) が発生すると，モデルの (b) が低下する。

また，学習データを複数に分割し，性能を評価する方法として

(d) が用いられる。

さらに，学習途中で性能の悪化を検知し学習を停止する手法を (e) という。

(a)～(e) に入る語句を記せ。

4-练习（日语版本）解析

【模擬問題①】問題1（強化学習・MDP）

アンサー：

(a) マルコフ性

中文：马尔可夫性（只与当前状态和行动有关）
(b) マルコフ決定過程（MDP）

中文：马尔可夫决策过程
(d) 割引率

中文：折扣率（γ）
(e) ベルマン最適方程式

中文：贝尔曼最优方程
(f) ベルマン

中文：贝尔曼（人名，用于方程名称）

【模擬問題②】問題2（教師あり学習・最適化）

アンサー：

(a) 正解ラベル

中文：正确标签
(b) 損失関数（誤差関数）

中文：损失函数（误差函数）
© 勾配

中文：梯度
(d) 学習率

中文：学习率
(e) 局所最小値

中文：局部最小值
(f) 正則化

中文：正则化

【予測問題①】問題3（確率的推論・不確実性）

アンサー：

(a) ノイズ

中文：噪声
(b) 確率分布

中文：概率分布
(d) 状態遷移モデル

中文：状态转移模型
(e) 尤度

中文：似然（likelihood）
(f) 正規化

中文：归一化

【予測問題②】問題4（汎化性能・学習限界）

アンサー：

(a) 過学習（オーバーフィッティング）

中文：过拟合
(b) 汎化性能

中文：泛化性能
(d) 交差検証

中文：交叉验证
(e) 早期終了（Early Stopping）

中文：提前停止学习

✅ 一页速记版（考前用）

复制代码

マルコフ性 / MDP / 報酬関数 / 割引率 / ベルマン方程式
正解ラベル / 損失関数 / 勾配 / 学習率 / 正則化
ノイズ / 確率分布 / 観測更新 / 正規化
過学習 / 汎化性能 / 交差検証 / 早期終了

5-単語练习（日语版本）

6-总结

知识一点点记录吧，最后应对考试，打下基础