BCQ: Batch-Constrained Q-learning
离线强化学习开篇之作 BCQ,针对离线场景外推泛化误差问题,通过生成 + 扰动的批次约束策略。
BCQ 以 CVAE 为生成模型拟合批次数据分布、Actor 为扰动模型做局部动作优化、双 Q 网络实现无偏价值评估,
三者协同让策略仅访问与缓冲区 Buffer 相似的(s,a)对,有效规避分布外数据误差。
同时详解算法代码实现细节,包括 VAE、Actor、Critic 的网络设计与训练流程。
目录
[1. 离线强化学习](#1. 离线强化学习)
[2. 离线核心问题:外推泛化误差 Extrapolation Error](#2. 离线核心问题:外推泛化误差 Extrapolation Error)
[3. BCQ: Batch-Constrained Q-learning 摘要](#3. BCQ: Batch-Constrained Q-learning 摘要)
[4. 生成+扰动:只访问与数据集中相似的 (s,a) 数据](#4. 生成+扰动:只访问与数据集中相似的 (s,a) 数据)
[5. 伪代码 - 代码](#5. 伪代码 - 代码)
[1. VAE (s,a) -> a' 编码器 + 解码器](#1. VAE (s,a) -> a' 编码器 + 解码器)
[2. Actor(扰动模型)动作优化器 (s,a) -> a'](#2. Actor(扰动模型)动作优化器 (s,a) -> a')
[3. 双 Q 同 TD3 的实现](#3. 双 Q 同 TD3 的实现)
[4. agent 组件初始化 + 训练完agent 的动作选择](#4. agent 组件初始化 + 训练完agent 的动作选择)
[5. agent.train()](#5. agent.train())
1. 离线强化学习
在线训练:智能体在训练过程中可以不断和环境交互 ,得到新的反馈数据。
on-policy 数据只跑一遍; off-policy 经验回放池
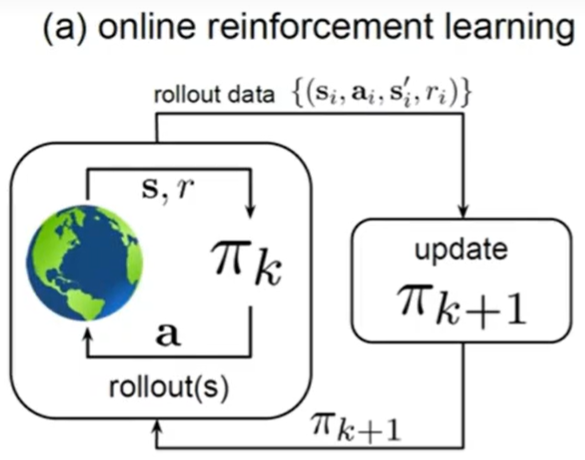
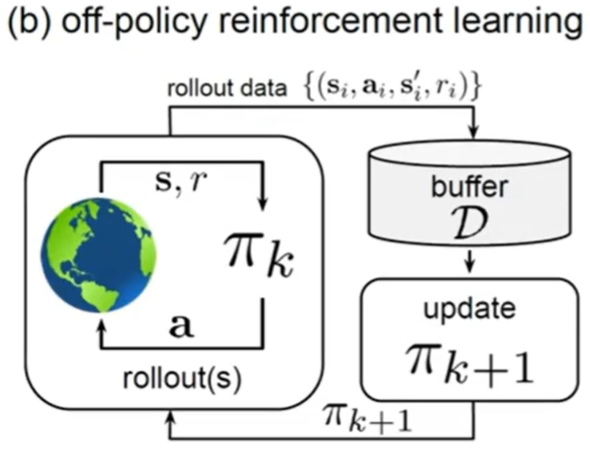
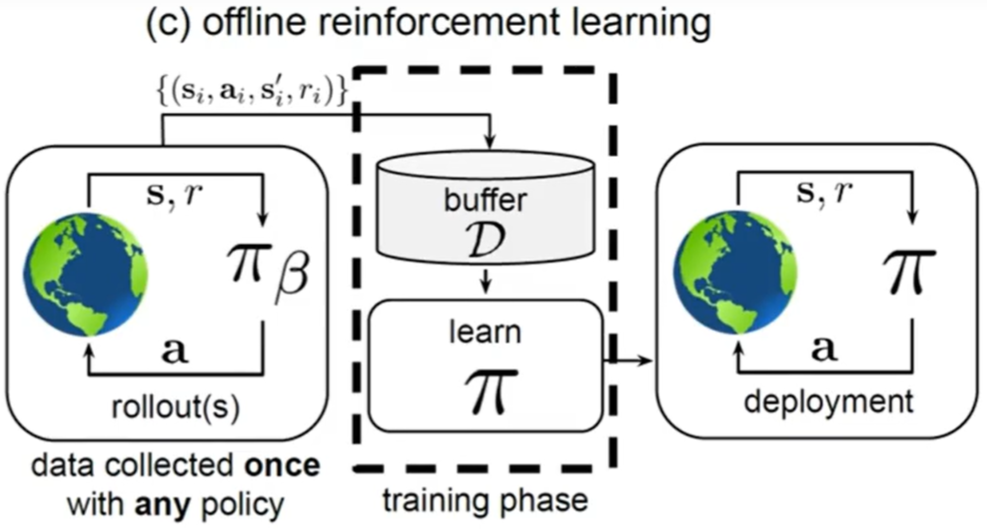
离线训练:不能让没训练好的 agent 直接和环境交互(比如自动驾驶 和 医疗)
只能和 buffer 中已有的数据交互。(像有监督学习那样)
- Behavior Cloning / Imitation Learning 行为克隆 / 模仿学习
局限性:1. compounding error 每一步误差累积 成更大的错误 2. 效果上限 就是专家本身
-
Model-based:不能直接和 env 交互,就搭建一个仿真环境 和仿真环境交互。
-
Model-free:训练时 显式/隐式 设置训练策略和 buffer 数据偏差不大。
2. 离线核心问题:外推泛化误差Extrapolation Error
-
Absent Data 数据缺失(当前训练策略访问的(s,a) 是 buffer 里没有的数据)
-
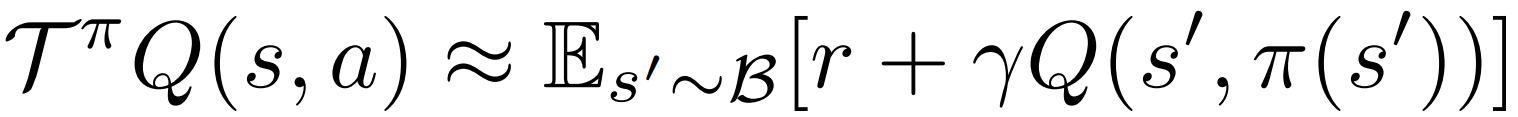
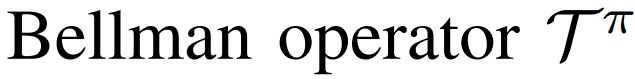 右边的期望 基于批次数据集 B 中的经验转移。若(s,a)较少 偏差。
右边的期望 基于批次数据集 B 中的经验转移。若(s,a)较少 偏差。
- 损失函数的权重与批次数据的出现概率相关
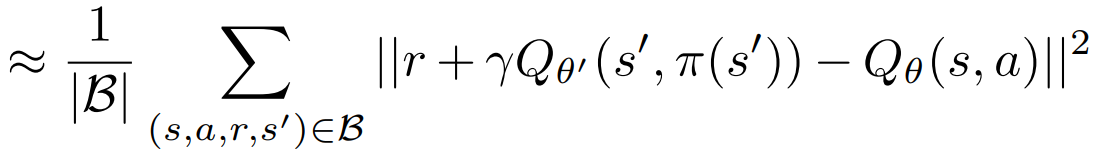
倘若数据集中不存在当前策略下高概率出现的 (s, a) 对,
最终的价值估计结果仍会存在较大误差。这意味着,我们仅能对一部分特定的策略进行准确评估。
而在线强化学习,即使训练是离线策略的,智能体依然有机会通过与环境交互 及时采样到新的数据 ,从而修正这些误差。
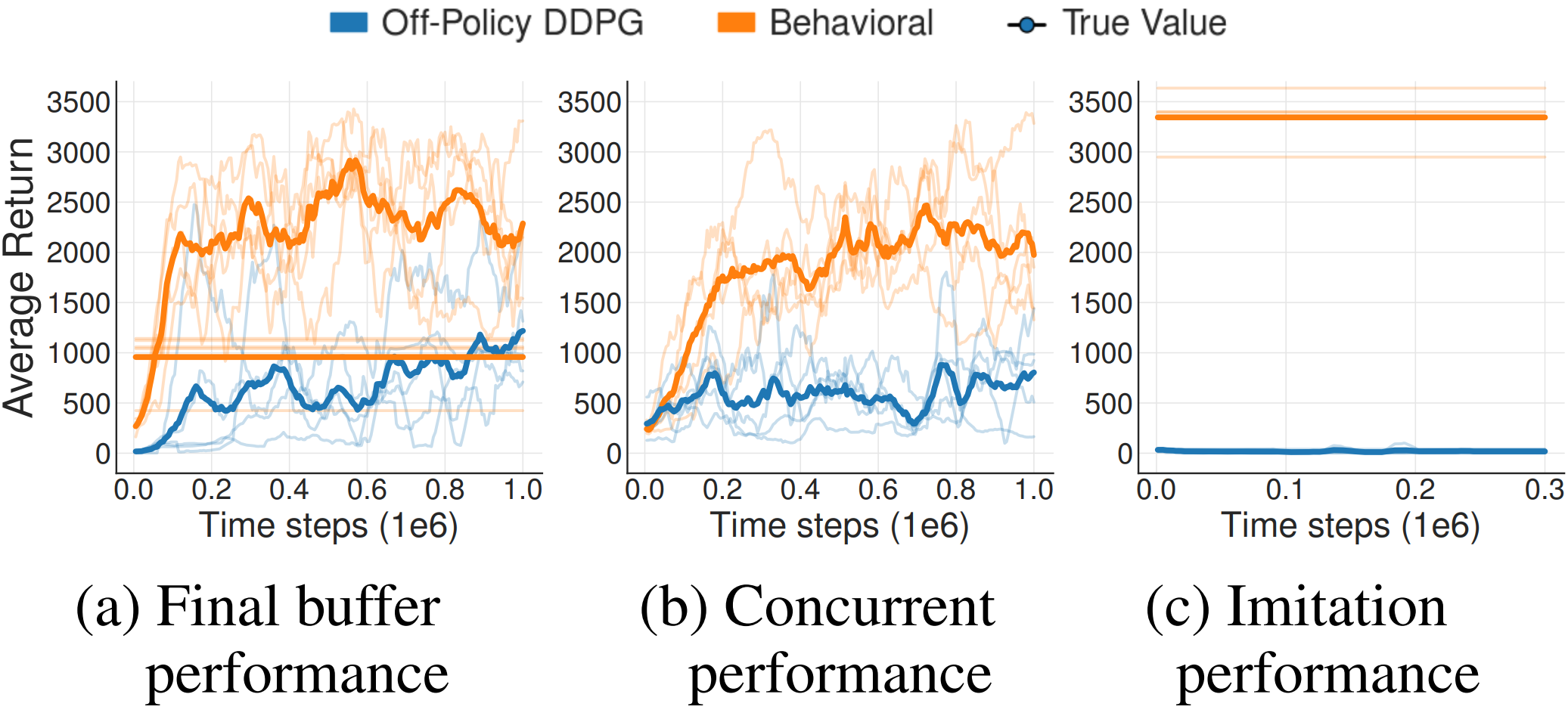
三组实验分别:
-
离线用 之前 训 DDPG 过程中收集的一批 buffer;
-
行为和离线一起训练 离线用行为的 buffer;
-
训练完成的 DDPG 作为专家 采100w步经验转移数据;
3. BCQ: Batch-Constrained Q-learning 摘要
对于那些数据采集过程成本高昂、存在风险或耗时长久的任务而言,
1. 批次强化学习 是实现强化学习规模化应用的关键前提。
由于"外推误差 " 当数据集 与当前策略对应的真实分布不相关时,算法的训练就无法成功。
-
无法为 选择批次数据集B 中未包含动作(s,a)的策略,学习有效的价值函数。
-
采用一个状态条件生成模型 来仅生成数据集中曾出现过的动作。
该生成模型与 Q 网络相结合,从而筛选出与批次数据特征相近且价值最高的动作。
- 我们的算法为模仿学习和离策略学习提供了统一的研究视角,不仅能够基于纯专家示范数据进行学习,
还可以利用有限的非最优批次数据完成训练,且无需开展额外的探索操作。
4. 生成+扰动:只访问与数据集中相似的 (s,a) 数据
减少外推误差 只访问与数据集中相似的 (s,a) 数据。
batch-constrained policy 批次约束策略:
(1) 选择的 a 接近 buffer 中已有的 a(后两者的基础)
(2) 引导到 相似数据buffer中有 的状态
(3) 最大化价值函数
表格形式:仅从 buffer 数据集中存在的动作中选择最优动作 argmax

高维/连续空间下 为了满足 buffer 约束:
在状态 s 下生成+扰动;得到几个距离 buffer 很近的 (s,a) 再通过 Q 网络 argmax
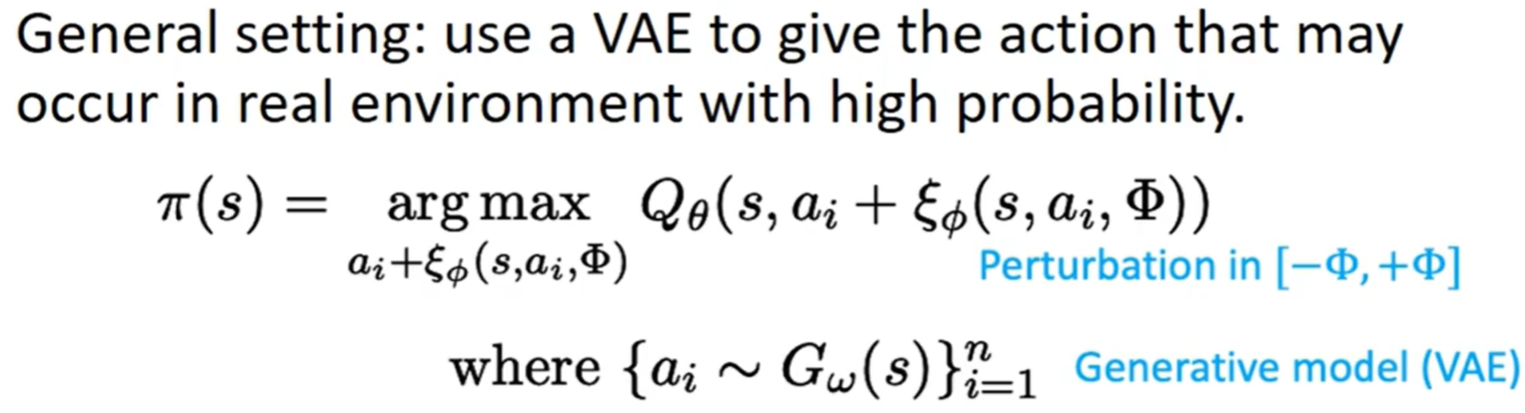
三大类组件:生成器 G;扰动器 ξ ;两个 Q 网络

相似性度量准则 similarity metric:(s,a) 对 是否与 B 相似 -> 状态条件边缘似然
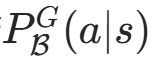 在批次缓冲区B的数据集分布下,给定状态 s 时,动作 a 出现的概率。
在批次缓冲区B的数据集分布下,给定状态 s 时,动作 a 出现的概率。
越高说明 (s,a) 与 B 越相似;低的话 就是 OOD(分布外数据)
生成模型G(s) 的目标:学习批次缓冲区B的动作分布 ,能够基于状态 s,生成 高相似性 动作。
(使用 条件变分自编码器(CVAE))
扰动模型:提升动作多样性 限制在[−Φ,Φ]内的调整。
可在约束动作空间 的前提下,覆盖更多合理动作 ,避免为获取足够动作多样性 而对生成模型进行大量采样。
最终 确定性策略为:(生成+扰动) 得到的候选动作中 -> 选 Q 最高的
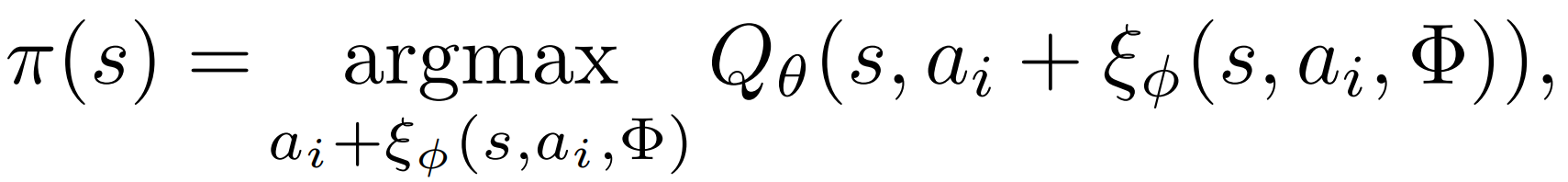
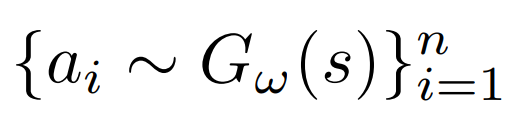
扰动模型 ξ 通过确定性策略梯度算法训练,目标是最大化 Q 网络的价值估计
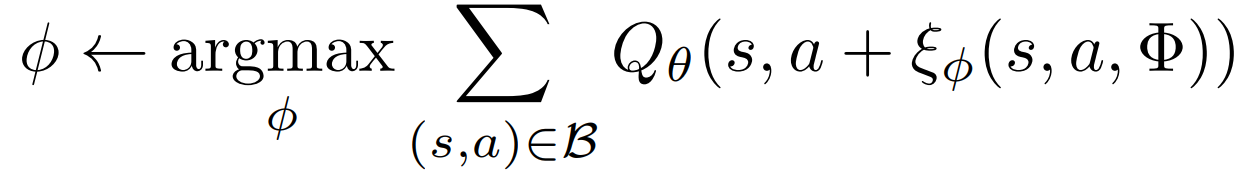
5. 伪代码 - 代码
VAE:(s,a) -> a 生成 符合批次数据分布的基础动作,保证动作的接近 Buffer;
Actor:对 VAE 生成的基础动作进行小幅度扰动优化 ,在合理范围内提升动作的 "价值";
Critic:双Q;准确评估状态 - 动作对的价值
1. VAE (s,a) -> a' 编码器 + 解码器
编码器 (s,a) -> latent_dim 维度的 z
python
class VAE(nn.Module):
def __init__(self, state_dim, action_dim, latent_dim, max_action, device):
super().__init__()
# 编码器网络:输入(状态+动作),输出潜在空间的均值和标准差
self.e1 = nn.Linear(state_dim + action_dim, 750)
self.e2 = nn.Linear(750, 750)
self.mean = nn.Linear(750, latent_dim)
self.log_std = nn.Linear(750, latent_dim) # 对数标准差; 取指数以确保标准差为正值
# 解码器网络:输入(状态+潜在变量),输出生成的动作
self.d1 = nn.Linear(state_dim + latent_dim, 750)
self.d2 = nn.Linear(750, 750)
self.d3 = nn.Linear(750, action_dim)
self.max_action = max_action
self.latent_dim = latent_dim
self.device = device解码器 (s,z) -> a';完整的 VAE 由编码器得到 z;
在下方 agent.select_action 中,通过N~(0,1) 采样不同的 z 得到不同的动作。
python
def decode(self, state, z=None):
# 没有z 直接s->a 从标准正态分布采样z,并裁剪到[-0.5, 0.5]
if z is None:
z = torch.randn((state.shape[0], self.latent_dim)).to(self.device).clamp(-0.5, 0.5)
a = F.relu(self.d1(torch.cat([state, z], 1)))
a = F.relu(self.d2(a))
return self.max_action * torch.tanh(self.d3(a))forward:(s,a) -> 编码器 -> z -> (s,z) -> 解码器 -> u
python
def forward(self, state, action):
z = F.relu(self.e1(torch.cat([state, action], 1)))
z = F.relu(self.e2(z))
mean = self.mean(z)
log_std = self.log_std(z).clamp(-4, 15) # 截断 -> 数值稳定
std = torch.exp(log_std)
z = mean + std * torch.randn_like(std) # 重参数化 在潜在分布中采样潜在变量z
u = self.decode(state, z)
return u, mean, std2. Actor(扰动模型)动作优化器 (s,a) -> a'
得到扰动范围内的 a;action + a 裁剪后作为最终 a'
python
class Actor(nn.Module):
def __init__(self, state_dim, action_dim, max_action, phi=0.05):
super().__init__()
self.l1 = nn.Linear(state_dim + action_dim, 400)
self.l2 = nn.Linear(400, 300)
self.l3 = nn.Linear(300, action_dim)
self.max_action = max_action
self.phi = phi # 扰动幅度系数(对应论文中的Φ),控制扰动的最大幅度
def forward(self, state, action):
a = F.relu(self.l1(torch.cat([state, action], 1)))
a = F.relu(self.l2(a))
a = self.phi * self.max_action * torch.tanh(self.l3(a)) # 扰动值 在[-phi*max_action, phi*max_action]
return (a + action).clamp(-self.max_action, self.max_action) # 最终动作 裁剪在范围内3. 双 Q 同 TD3 的实现
python
class Critic(nn.Module):
def __init__(self, state_dim, action_dim):
super().__init__()
# Q1 architecture
self.l1 = nn.Linear(state_dim + action_dim, 400)
self.l2 = nn.Linear(400, 300)
self.l3 = nn.Linear(300, 1)
# Q2 architecture
self.l4 = nn.Linear(state_dim + action_dim, 400)
self.l5 = nn.Linear(400, 300)
self.l6 = nn.Linear(300, 1)
def forward(self, state, action):
q1 = F.relu(self.l1(torch.cat([state, action], 1)))
q1 = F.relu(self.l2(q1))
q1 = self.l3(q1)
q2 = F.relu(self.l4(torch.cat([state, action], 1)))
q2 = F.relu(self.l5(q2))
q2 = self.l6(q2)
return q1, q2
def q1(self, state, action):
q1 = F.relu(self.l1(torch.cat([state, action], 1)))
q1 = F.relu(self.l2(q1))
q1 = self.l3(q1)
return q14. agent 组件初始化 + 训练完agent 的动作选择
python
class BCQ(object):
def __init__(self, state_dim, action_dim, max_action, device, discount=0.99, tau=0.005, lmbda=0.75, phi=0.05):
latent_dim = action_dim * 2 # 隐变量维度
self.actor = Actor(state_dim, action_dim, max_action, phi).to(device)
self.actor_target = copy.deepcopy(self.actor)
self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=1e-3)
self.critic = Critic(state_dim, action_dim).to(device)
self.critic_target = copy.deepcopy(self.critic)
self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=1e-3)
self.vae = VAE(state_dim, action_dim, latent_dim, max_action, device).to(device)
self.vae_optimizer = torch.optim.Adam(self.vae.parameters())
self.max_action = max_action
self.action_dim = action_dim
self.discount = discount
self.tau = tau
self.lmbda = lmbda
self.device = device完成训练后 使用时的动作选择:每个状态 通过 z 的采样,得到一百个动作,取 q1.argmax()
python
def select_action(self, state):
with torch.no_grad():
state = torch.FloatTensor(state.reshape(1, -1)).repeat(100, 1).to(self.device) # [100, state_dim] 的批量 state
action = self.actor(state, self.vae.decode(state)) # 根据N~(0,1)采样的z得到100个动作,再actor扰动优化
q1 = self.critic.q1(state, action)
ind = q1.argmax(0) # 每个状态选择第0维(100个动作中) Q值最大的动作
return action[ind].cpu().data.numpy().flatten()5. agent.train()
- 采样批次数据训练 G 生成模型(VAE 包含 E 和 D)
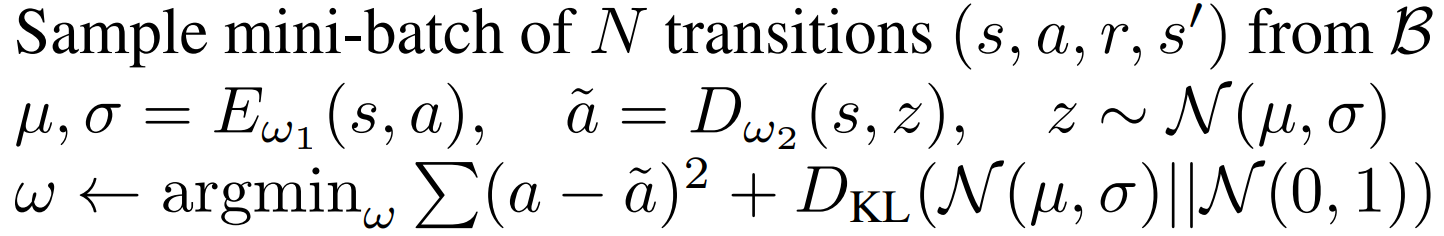
- 编码器 E 对输入的状态 - 动作对 (s,a) 编码,得到潜在变量的均值 μ 和标准差 σ。
- 解码器 D 从潜在分布 N(μ,σ) 采样 z,并解码生成动作 ã。
损失函数由两部分组成:
- 重建 损失 ∑(a − ã)²:确保生成的动作与原始动作尽可能相似 ,对应理论中 "生成与批次数据相似的动作" 的要求。
- KL 散度损失 D_KL(N(μ,σ)||N(0,1)):约束潜在分布接近标准正态分布 ,防止模型过度拟合样本,提升生成动作的泛化性。
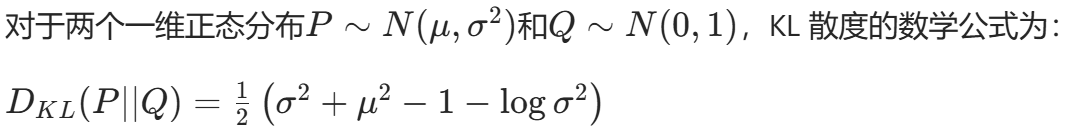
python
def train(self, replay_buffer, iterations, batch_size=100):
for it in range(iterations):
# Sample replay buffer / batch
state, action, next_state, reward, not_done = replay_buffer.sample(batch_size)
# Variational Auto-Encoder Training
recon, mean, std = self.vae(state, action)
recon_loss = F.mse_loss(recon, action) # 重构损失
KL_loss = -0.5 * (1 + torch.log(std.pow(2)) - mean.pow(2) - std.pow(2)).mean() # KL散度损失
vae_loss = recon_loss + 0.5 * KL_loss # 总体VAE损失
self.vae_optimizer.zero_grad()
vae_loss.backward()
self.vae_optimizer.step()- 训练 Q;用 s' 生成动作 得到 Q(s', a') 作为 TD target
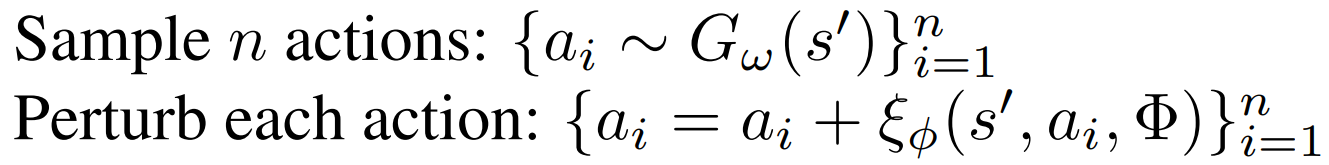
target:Clipped Double Q-learning 裁剪双 Q 学习 作为 TD target
TD3里就是 min; 这里用:min 高权重 + max 低权重。
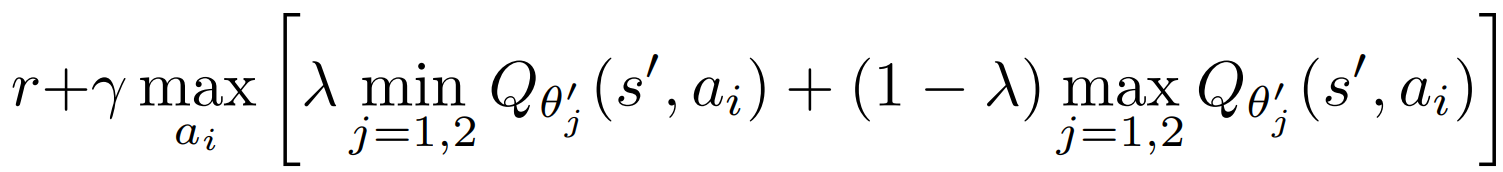
python
with torch.no_grad():
# 复制10个s'
next_state = torch.repeat_interleave(next_state, 10, 0)
# Compute value of perturbed actions sampled from the VAE
target_Q1, target_Q2 = self.critic_target(next_state,
self.actor_target(next_state, self.vae.decode(next_state)))
# 最小最大加权 Clipped Double Q-learning
target_Q = self.lmbda * torch.min(target_Q1, target_Q2) + (1. - self.lmbda) * torch.max(target_Q1, target_Q2)
target_Q = target_Q.reshape(batch_size, -1).max(1)[0].reshape(-1, 1) # Q*
target_Q = reward + not_done * self.discount * target_Q
current_Q1, current_Q2 = self.critic(state, action)
critic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()- 更新 Q 和 生成模型 G;并软更新
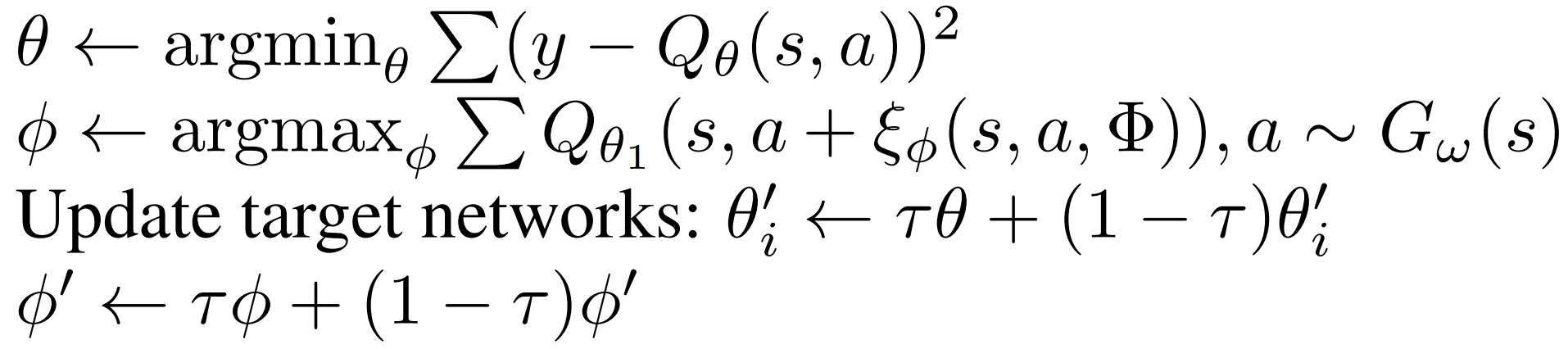
扰动模型 ξ 通过 DDPG目标函数 训练,目标是最大化 Q 网络的价值估计(类似 TD3 只用Q1)
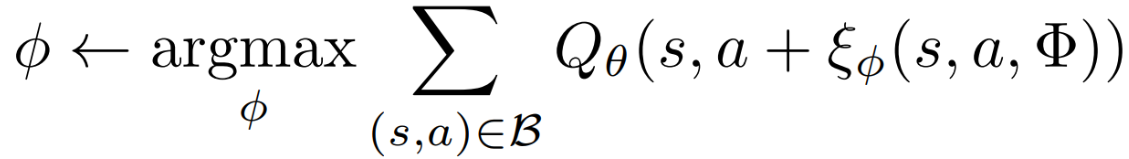
python
# 训练 actor
actor_loss = -self.critic.q1(state, self.actor(state, self.vae.decode(state))).mean()
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# 软更新
for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)
for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
target_param.data.copy_(self.tau * param.data + (1 - self.tau) * target_param.data)实验使用:DDPG 先得到 Buffer;再用 Buffer 训 BCQ.