深度学习学习技巧总结

深度学习的核心是让模型高效学到数据规律，而实际工作中常遇到训练慢、过拟合、梯度不稳定等问题。本章聚焦工程中最常用的学习技巧，用通俗的语言拆解核心逻辑和实操方法。

一、先解决核心痛点：梯度消失 / 爆炸

深度神经网络训练时，容易出现 "梯度消失 "（前面层的参数几乎不更新）或 "梯度爆炸"（参数值异常过大导致模型崩溃），这是深层模型的常见问题。

关键原因

反向传播时，梯度会逐层传递并乘以系数，系数小于 1 则梯度越传越小（消失），大于 1 则越传越大（爆炸）。

实用解决方法

选对激活函数：隐藏层优先用 ReLU，避免 Sigmoid（极易梯度消失）；若 ReLU 出现 "神经元死亡"，换用 Leaky ReLU。
合理初始化参数：用 Xavier 初始化搭配 Sigmoid/Tanh，He 初始化搭配 ReLU/Leaky ReLU，避免权重过大或过小。
用 Batch Normalization（BN 层）：放在线性层之后、激活函数之前，自动调整数据分布，让梯度稳定传递，还能加速训练。

二、参数更新：比 SGD 更高效的优化方法

参数更新的目标是快速找到损失函数的最小值，SGD 虽基础但效率低，工作中更常用以下优化器：

1. 动量法（Momentum）

核心逻辑：模拟物理中的 "惯性"，积累历史梯度方向，避免训练时来回震荡。
适用场景：损失函数曲面崎岖、震荡明显的任务（如图像分类）。
关键参数：动量值（通常设 0.9），平衡历史梯度和当前梯度的影响。

class Momentum:
"""
动量优化
"""
#初始化
def init(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
#更新参数
def update(self, params, grads): # 参数和梯度
if self.v is None: # 如果动量参数v是None，则初始化动量参数v
self.v = {}
for i in params.items(): # 遍历参数的键和值
self.v[i] = np.zeros_like(params[i]) # 初始化动量参数v为0
复制代码
```
      for i in params.keys():         # 遍历参数的键
          self.v[i] = self.momentum * self.v[i] - self.lr * grads[i]
          params[i] += self.v[i]
```

2. 自适应学习率方法

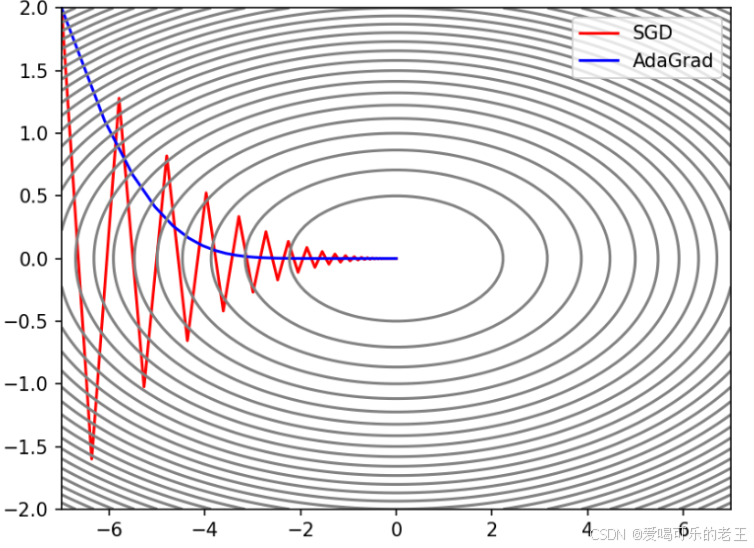
AdaGrad（Adaptive Gradient 自适应梯度）：为每个参数单独调整学习率，适合稀疏数据（如文本分类),但后期学习率会过小，如果无止境学习，更新量就会变为0，完全不再更新.

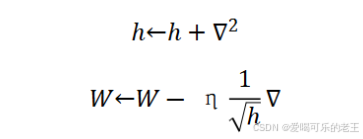
h 是一个 "辅助变量"（可以理解为记录 "梯度平方累积值" 的缓存）；
∇2 是当前参数梯度的平方值（∇ 是参数的梯度，代表参数更新的方向）。
W 是模型的待更新参数（比如神经网络的权重）；
η 是学习率（控制参数更新的步长，工作中常用 0.001、0.01 等）；
是 "自适应缩放因子"（用之前累积的梯度平方的平方根来 "校准" 当前梯度）；
∇ 是当前参数的梯度（参数需要沿着梯度的反方向更新，所以是 "减号"）。

代码实现：

复制代码

class AdaGrad:
    """
    自适应梯度
    """
    #初始化
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self,params,grads):
        if self.h is None:
            # 初始化
            self.h = {}
            for key,val in params.items(): # 遍历参数的键和值
                # 为每个参数（W, b等）创建一个全0数组，形状与参数一致
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            # 累加梯度的平方
            self.h[key] += grads[key] * grads[key]
            # 更新参数
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

RMSProp：改进 AdaGrad，遗忘遥远的历史梯度，避免学习率过早停滞。
Adam（最常用）：融合 Momentum 和 RMSProp 的优点，自适应调整学习率和动量，几乎适用于所有任务（推荐默认使用）。

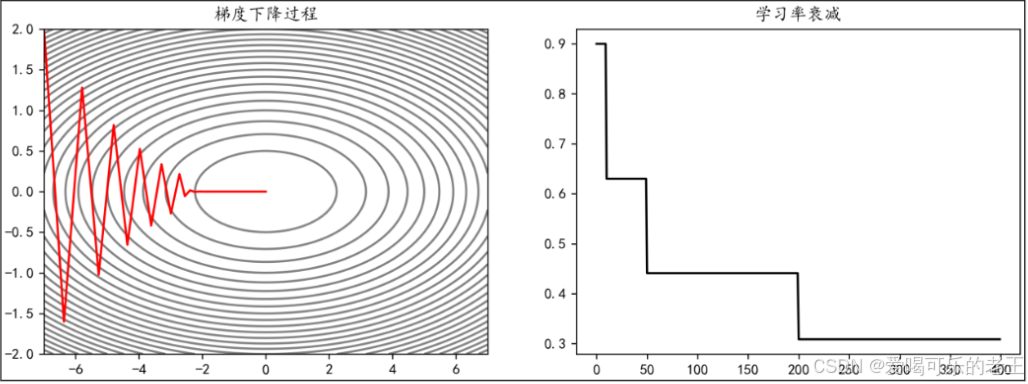
3. 学习率衰减

核心逻辑：训练初期用较大学习率快速逼近最优解，后期减小学习率精细调整。
常用方式：
- 等间隔衰减：每训练一定 epoch（如 20 轮），学习率乘以衰减系数（如 0.7）。

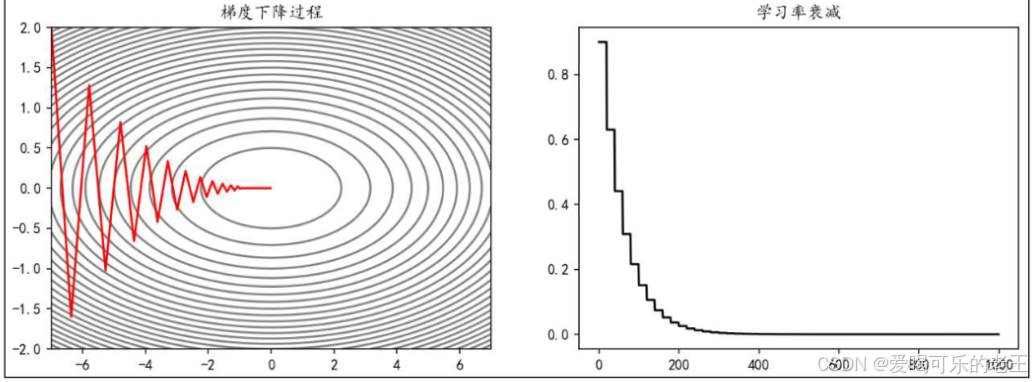
指数衰减：学习率随 epoch 呈指数下降（如 0.99^epoch），适合需要长期训练的任务。

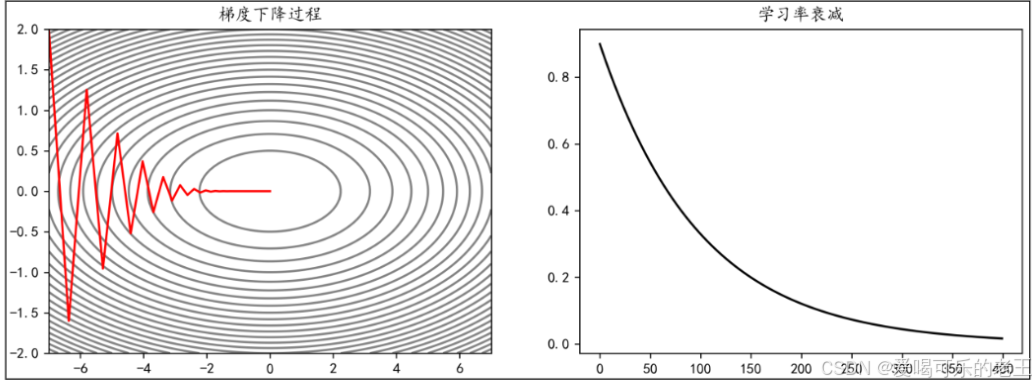
指定衰减：在指定的 epoch,让学习率按照一定的系数衰减。例如,使学习率在 epoch达到[10,50,200]时衰减为之前的0.7:

三、参数初始化：开局决定训练难度

参数初始化不当会直接导致训练失败，工作中无需自己写公式，记住以下常用方案即可：

初始化方法	适用场景	核心逻辑
正态分布初始化	简单模型快速验证	权重从均值 0、标准差 0.01 的正态分布中采样
Xavier 初始化	Sigmoid/Tanh 激活函数	让输入输出方差一致，避免梯度消失
He 初始化	ReLU/Leaky ReLU 激活函数	适配 ReLU 的输出分布，防止神经元死亡

避坑提醒

绝对不要把权重初始化为 0 或相同值，会导致所有参数更新一致，模型无法学习。
偏置参数通常初始化为 0，简单且效果稳定。

四、正则化：解决过拟合的核心手段

过拟合是工作中最常见的问题 ------ 模型在训练数据上表现极好，但在新数据上效果差，本质是模型 "学了数据中的噪声"。以下是工程中最常用的 3 种正则化方法：

1. 权值衰减（L2 正则化）

核心逻辑：给损失函数加 "惩罚项"，让权重参数尽量小，避免模型过度依赖某些特征。
实操方法：在优化器中设置权重衰减系数（如 0.001），框架会自动计算惩罚项，无需手动修改损失函数。
适用场景：所有有过拟合风险的任务（如回归、分类）。

2. Dropout（随机失活）

核心逻辑：训练时随机 "关闭" 部分神经元，让模型不依赖单个神经元，增强鲁棒性。
实操细节：
- 训练时：隐藏层设置失活概率（通常 0.2-0.5），激活的神经元输出需除以（1 - 失活概率）。
- 测试时：不关闭任何神经元，无需调整输出（框架会自动处理）。
适用场景：全连接层、大规模神经网络（如图像识别、NLP）。

3. 早停法（Early Stopping）

核心逻辑：训练时监控验证集的性能，当验证集准确率不再提升（或损失不再下降）时，停止训练，避免继续学习噪声。
实操方法：设置 "耐心值"（如 10 轮），若 10 轮内验证集性能无改善，就停止训练并保存最优模型。

五、工作中的优先级建议

新手入门：先用 Adam 优化器 + ReLU 激活函数 + He 初始化，基本能应对 80% 的任务。
出现过拟合：先加 Dropout（失活概率 0.3），再使用权值衰减（0.001），最后用早停法。
训练不稳定：加入 BN 层，搭配学习率衰减（等间隔衰减，每 20 轮衰减为 0.7 倍）。
数据稀疏：用 RMSProp 或 AdaGrad 优化器，提升参数更新的针对性。