"||x||"符号在机器学习算法中随处可见，但它背后的实际直觉是什么呢？
勾股定理是一个很好的切入点。这当然是每个人在几何课上都学过的内容，但这里还是简单回顾一下，方便大家入门：
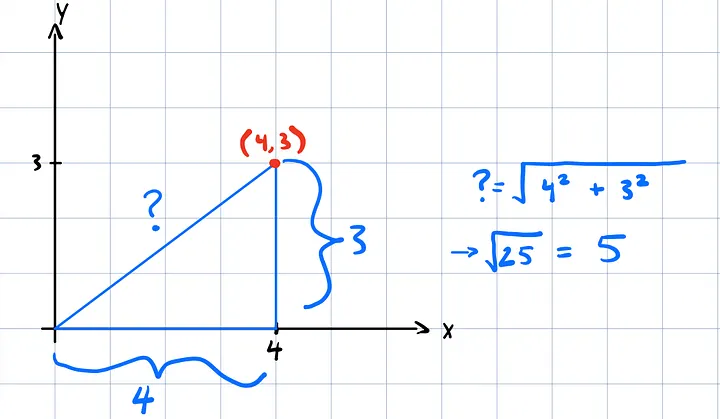
图中高亮显示的点 (4,3) 被分解成两个方向分量 -> (4,0) 和 (0,3)：
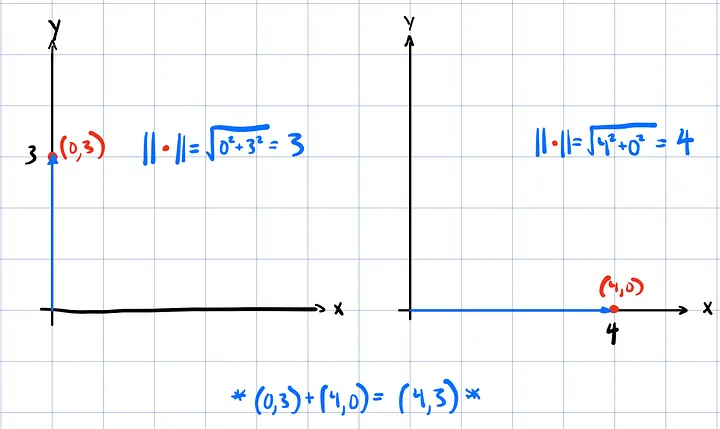
这些方向分量使量级的概念更容易理解。这些分量的大小就是它们到原点的距离，而这正是量级公式有效的原因。
通过将这些分解分量相加，我们得到了原点 (4,3)。因此，从 (0,0) 到 (4,3) 的线段长度就是各个分量之和的模！虽然这段描述略显冗长，但它完美地过渡到了欧几里得范数（也称为 L2 范数）的正式定义：
这张图在讲 范数 ，而在实数向量空间
里，
范数就是我们常说的 欧氏范数（Euclidean norm）------也就是"向量的长度"。
1) 图里在做什么：从向量到"长度"
图中先把向量写成列向量：
然后给出它的 L2 范数（也写作 范数、2-范数）：
这就是欧氏范数的定义（在实数情况下就是最常见的"勾股定理推广"）。
- 如果
是实数 ，
图里用三维举例：
这就是三维空间里"点到原点的直线距离"。
2) 为什么叫"欧氏"：它对应我们熟悉的几何距离
在二维平面里，点 (x1,x2) 到原点的距离是：
三维是：
推广到 n 维就是图里的式子。所以它叫"欧氏"（Euclid）------对应我们直觉里的直线距离。
更一般地，两点 a,b 的欧氏距离就是：
3) 图里提到复数：为什么要写
如果向量分量是复数 ，直接平方会出"方向/相位"的麻烦，所以用模长平方：
- 若
因此
也可以写成（更线性代数的形式）：
其中 是共轭转置（实数情况下就是
）。
4) 图最后的"函数版 L2"：从求和变积分
图里还说"大写 L2"常保留给函数空间：
你可以把它理解成：
-
离散向量 ：把每个分量的"能量"
-
连续函数 ：把每一点的"能量密度"
所以它们本质上是同一件事：平方 → 累加 → 开方。
5)在正交矩阵中的应用
该公式是正交矩阵最核心的性质之一：它保持向量的长度（欧氏范数）不变。
这看起来一串矩阵运算，其实超级简单，就是在证明"旋转或反射后，向量长度没变"。就像你拿一根棒子转来转去，或者照镜子，棒子长度始终一样。
我们一步步拆开，每步都解释为什么：
步骤1：向量长度平方怎么算？
- 一个向量
- 长度平方就是
- 用矩阵写法：这就是
- 同理，变换后的向量 Qx 的长度平方是
- 这步就是定义：任何向量的长度平方 = 它转置乘它自己。
步骤2：矩阵转置的"反向"规则
- 矩阵乘法的转置有个重要性质：
- 所以
- 代入得：
- 再把 Qx 带进去：
- 这里用了结合律：矩阵乘法可以"括号移动"。
步骤3：正交矩阵的"杀手锏"------
- 正交矩阵的定义就是
- 所以直接代入：
- 单位矩阵乘任何东西都不变：
- 所以
完事！整个证明就靠这三步：定义 + 转置规则 + 正交定义。
用最简单的2D例子算一遍（旋转矩阵）
拿经典旋转矩阵（转 θ 角）：
随便拿个向量，比如 （长度5，因为3-4-5直角三角形）
-
原长度平方：
-
变换后 Qx：假设 θ=90°（cos90=0, sin90=1）
-
新长度平方：
不管转多少度，都一样（因为 cos²θ + sin²θ = 1 的恒等式在起作用）。
反射也一样（带镜像的正交矩阵）
比如沿x轴反射：
→
长度平方还是 9 + 16 = 25。就像镜子里的你，身高没变，只是左右翻了。
为什么这个性质这么重要？
- 几何上：旋转、反射就是"刚体运动"，不拉伸、不压缩。
- 实际用：图形学里转模型不走样；数值计算里正交矩阵不会放大误差（保持数值稳定）；量子力学里能量（长度平方）守恒。
- 扩展：它不只保持长度，还保持角度（内积不变，证明类似：
脑补画面：想象一根箭头（向量），乘上正交矩阵后，只是方向变了（旋转或翻转），箭头长短完全一样。非正交矩阵就会把箭头拉长或压短。
一句话：正交变换不会改变欧氏长度。
6) 不只是"长度不变"，连"距离"和"角度"都不变
距离不变
两点距离是 。
正交变换后：
所以 所有点与点的距离都保持，这就是"刚体运动"的数学版本。
角度不变
角度来自点积公式：
正交变换后点积也保持：
同时长度也保持，所以 cosθ 不变，角度就不变。
结论：正交矩阵 = 保距离 + 保角度 的变换（旋转或旋转+镜像）。