33节点直流配电网网牛顿拉夫逊法(牛拉法)潮流计算MATLAB程序,采用有名值计算,最后可以得出各节点电压和各支路功率。 注意是直流配电网,交流网络改改也能使用,原理是一样的,程序简单易读,注释详尽,容易理解,适合新手。 运行结果如下图所示。
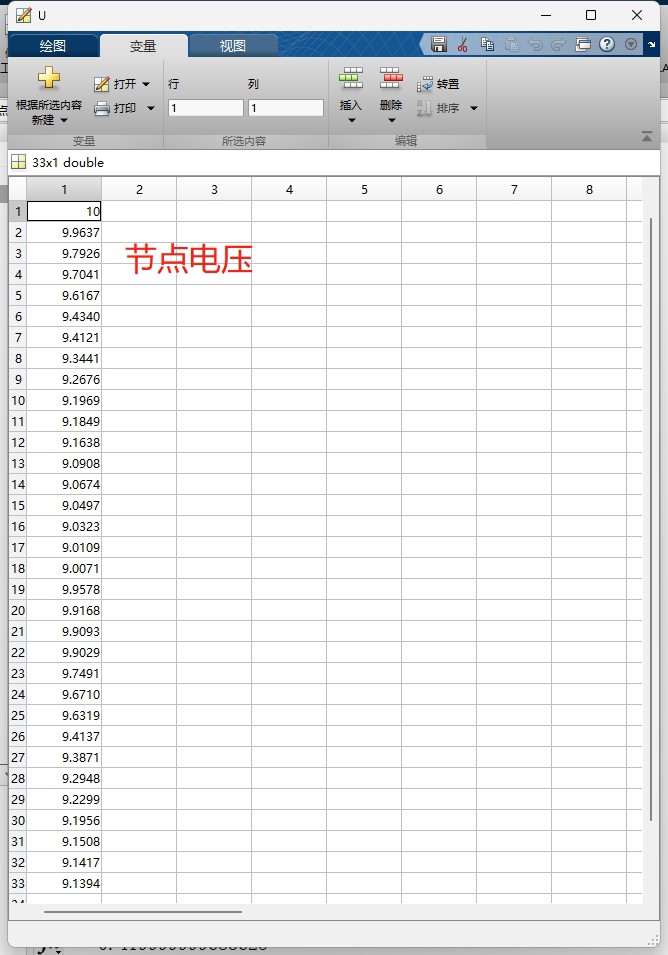
在电力系统分析中,潮流计算是一项至关重要的任务,它能够帮助我们了解系统中各节点的电压和各支路的功率分布情况。今天咱们就来讲讲基于牛顿拉夫逊法(牛拉法)的 33 节点直流配电网潮流计算,并且用 MATLAB 来实现,这个程序简单易读,注释详尽,新手友好哦。而且有趣的是,交流网络改改也能用,因为原理相通。
程序整体思路
牛顿拉夫逊法潮流计算的核心思想是通过迭代求解非线性方程组,逐步逼近潮流方程的精确解。对于直流配电网,其潮流方程相对交流电网要简单一些,主要涉及节点电压和支路功率的关系。
MATLAB 代码实现
matlab
% 33节点直流配电网牛顿拉夫逊法潮流计算
% 采用有名值计算
% 1. 网络参数设置
% 支路数据,格式:[始端节点 末端节点 电阻 电导]
branch_data = [
1 2 0.0922 0.0047;
1 3 0.4930 0.0207;
% 此处省略剩余支路数据......
32 33 0.2030 0.0085
];
% 节点数据,格式:[节点号 类型 P Q]
% 类型:1 - PQ节点,2 - PV节点,3 - 平衡节点
bus_data = [
1 3 0 0;
2 1 -0.217 0;
% 此处省略剩余节点数据......
33 1 -0.026 0
];
nb = size(bus_data, 1); % 节点数
nl = size(branch_data, 1); % 支路数
% 初始化节点电压
V = ones(nb, 1);
% 收敛判据
epsilon = 1e - 6;
max_iter = 100;
iter = 0;这段代码主要是在设置网络参数,包括支路数据和节点数据,然后初始化一些变量,比如节点电压 V,收敛判据 epsilon,最大迭代次数 max_iter 以及当前迭代次数 iter。这里的支路数据详细记录了每条支路的连接节点以及电阻和电导信息,节点数据则明确了每个节点的类型(PQ 节点、PV 节点还是平衡节点)以及注入的有功功率 P 和无功功率 Q。
matlab
while iter < max_iter
% 2. 计算雅克比矩阵和功率偏差
J = zeros(nb - 1, nb - 1);
dP = zeros(nb - 1, 1);
for i = 1:nb
if bus_data(i, 2) ~= 3 % 非平衡节点
Pii = 0;
for k = 1:nl
if branch_data(k, 1) == i
Pii = Pii + (V(i) - V(branch_data(k, 2))) * (V(i) - V(branch_data(k, 2))) * branch_data(k, 3);
elseif branch_data(k, 2) == i
Pii = Pii + (V(i) - V(branch_data(k, 1))) * (V(i) - V(branch_data(k, 1))) * branch_data(k, 3);
end
end
dP(i - (bus_data(i, 2) == 3)) = bus_data(i, 3) - Pii;
for j = 1:nb
if j ~= i
Pij = 0;
for k = 1:nl
if (branch_data(k, 1) == i && branch_data(k, 2) == j) || (branch_data(k, 1) == j && branch_data(k, 2) == i)
Pij = (V(i) - V(j)) * (V(i) - V(j)) * branch_data(k, 3);
break;
end
end
if bus_data(j, 2) ~= 3
J(i - (bus_data(i, 2) == 3), j - (bus_data(j, 2) == 3)) = -2 * (V(i) - V(j)) * branch_data(k, 3);
end
end
end
end
end这里进入了迭代计算部分,每次迭代都要计算雅克比矩阵 J 和功率偏差 dP。对于每个非平衡节点,先计算该节点的注入功率 Pii,与给定的注入功率 bus_data(i, 3) 比较得到功率偏差 dP。在计算雅克比矩阵元素时,考虑节点间通过支路的连接关系,根据电压差和支路电阻来确定。
matlab
% 3. 求解修正方程
dV = J \ dP;
% 4. 更新节点电压
for i = 1:nb - 1
V(i + (bus_data(i + 1, 2) == 3)) = V(i + (bus_data(i + 1, 2) == 3)) + dV(i);
end
% 5. 收敛判断
if norm(dP) < epsilon
break;
end
iter = iter + 1;
end这部分代码就是求解修正方程得到电压修正量 dV,然后更新节点电压 V。每次更新完后,通过判断功率偏差的范数 norm(dP) 是否小于收敛判据 epsilon 来决定是否停止迭代,如果小于就说明收敛了,跳出循环,否则继续迭代。
matlab
% 6. 计算各支路功率
branch_power = zeros(nl, 1);
for k = 1:nl
if branch_data(k, 1) < branch_data(k, 2)
branch_power(k) = (V(branch_data(k, 1)) - V(branch_data(k, 2))) * (V(branch_data(k, 1)) - V(branch_data(k, 2))) * branch_data(k, 3);
else
branch_power(k) = - (V(branch_data(k, 1)) - V(branch_data(k, 2))) * (V(branch_data(k, 1)) - V(branch_data(k, 2))) * branch_data(k, 3);
end
end
% 输出结果
fprintf('各节点电压:\n');
disp(V);
fprintf('各支路功率:\n');
disp(branch_power);最后这部分就是计算各支路功率,并输出各节点电压和各支路功率的结果啦。通过节点电压差的平方乘以支路电阻得到支路功率,根据支路方向确定功率的正负。
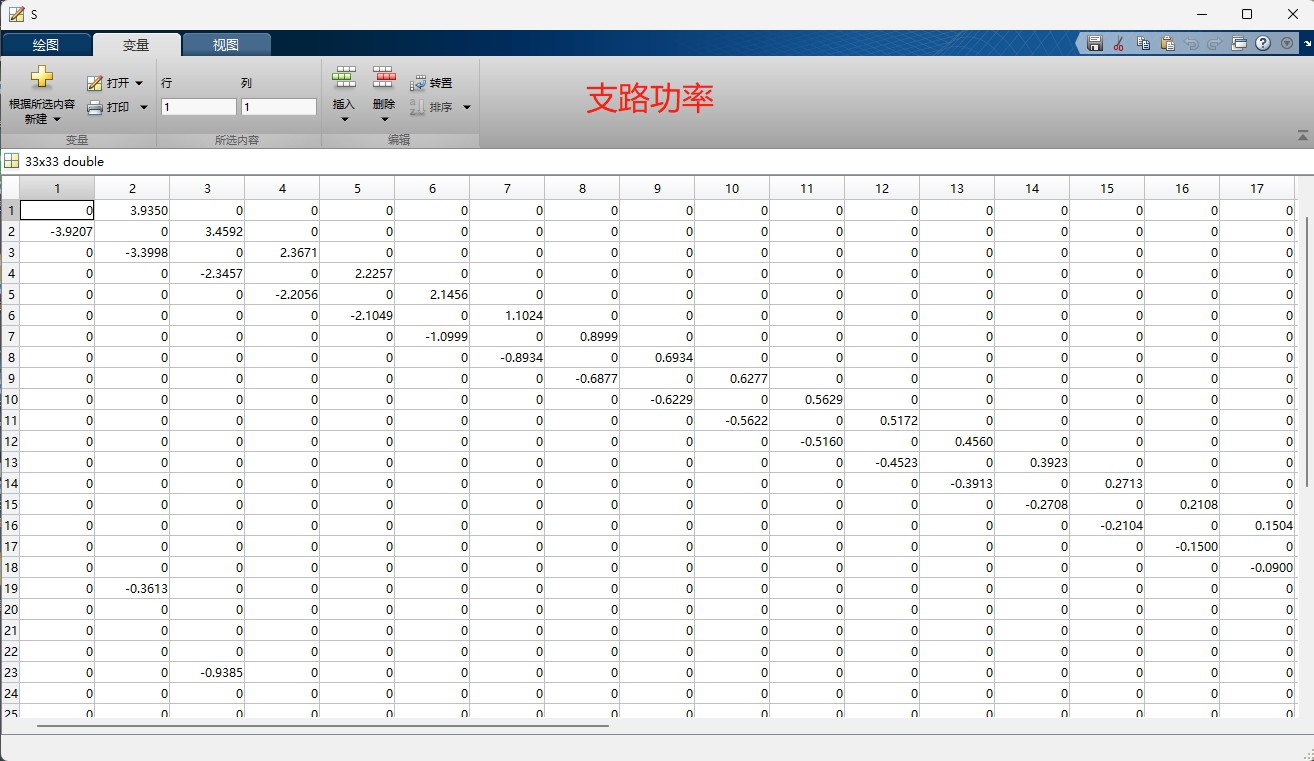
33节点直流配电网网牛顿拉夫逊法(牛拉法)潮流计算MATLAB程序,采用有名值计算,最后可以得出各节点电压和各支路功率。 注意是直流配电网,交流网络改改也能使用,原理是一样的,程序简单易读,注释详尽,容易理解,适合新手。 运行结果如下图所示。

运行这个程序后,就能得到如开头提到的运行结果图中所示的各节点电压和各支路功率啦,这对于分析 33 节点直流配电网的潮流分布非常有帮助,新手们可以多跑跑这个程序,加深对牛顿拉夫逊法潮流计算的理解哦。