leetcode hot100 148.排序链表 medium 递归 分治 | 冒泡排序

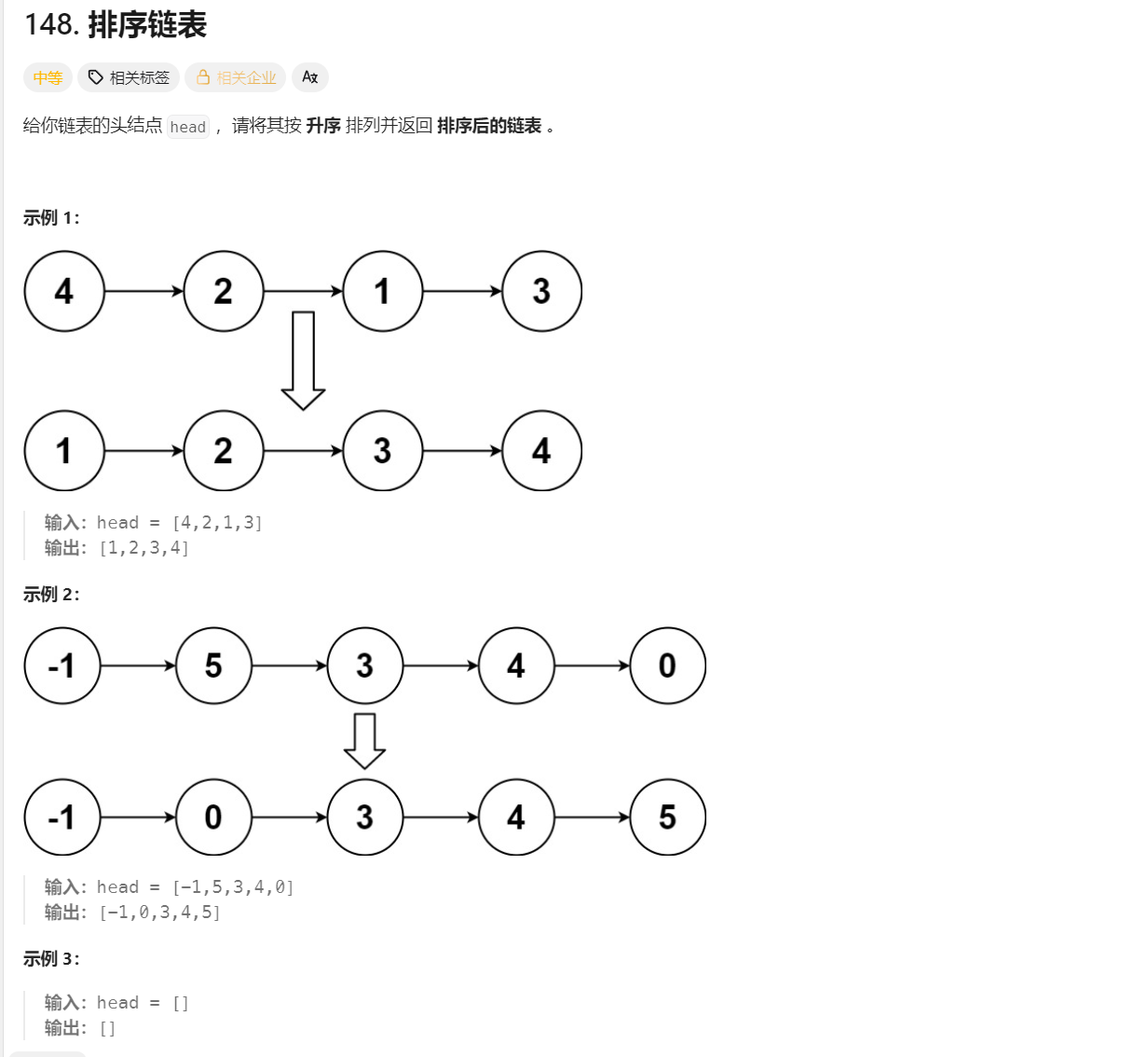
问题可以拆解为合并两个链表

在所有排序算法中，归并排序 （Merge Sort） 是最适合链表的

因为链表的"切分"和"合并"操作非常高效

核心思路 ：分治法 (Divide and Conquer)
归并排序分为三个阶段：

1. 递归切分 (Split) ：不断把大链表切成两半，直到每个小链表只剩一个节点（一个节点天然是有序的）。
2. 回归（Merge）：把两个有序的小链表合并成一个更大的有序链表，一级一级往回走。

为了找到中点，使用快慢指针

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:

        # 递归出口：如果为空或只有一个节点，无需排序
        if not head or not head.next:
            return head


        # 1. 找到中点并切断 (使用快慢指针)
        # slow 停在中点，pre 指向中点前一个节点用于切断
        slow  = head
        fast = head
        pre = None

        # fast指针会先走到终点
        while fast and fast.next:
            pre = slow
            slow = slow.next
            fast = fast.next.next

        # 切断链表，使其变成两个独立的链表
        pre.next = None 

        # 2. 递归排序左右两半
        left = self.sortList(head)  # 调用自己
        right = self.sortList(slow)

        # 3. 合并两个有序链表
        return self.merge(left, right)

    # def merge(self, l1: Optional[ListNode], l2: Optional[ListNode])  # 可以不写注释
    def merge(self, l1, l2):
        #新链表头
        prehead = ListNode(-1)
        dummy = prehead

        while l1 and l2:
            if l1.val <= l2.val:
                dummy.next = l1
                l1 = l1.next
            else:
                dummy.next = l2
                l2 = l2.next   

            dummy = dummy.next

        # 有一个链表已经用完
        if l1:
            dummy.next = l1
        else:
            dummy.next = l2 
        # 两个都空不用挂

        return prehead.next

时间复杂度： O ( n log ⁡ n ) O(n \log n) O(nlogn) 。每一层递归都要遍历 n n n 个节点进行合并，总共 log ⁡ n \log n logn 层。
空间复杂度 ： O ( log ⁡ n ) O(\log n) O(logn)。主要的开销是递归调用的栈空间。

---

内存与空间的差异

dummy.next = l1 (引用赋值)

动作：把 dummy.next 这根"指针线"指向了已经存在的 l1 节点。

空间： O ( 1 ) O(1) O(1)。没有创建任何新节点，只是改变了它们之间的连接方式。

dummy.next = ListNode(l1.val) (新建对象)

动作：在内存里新开辟了一块空间，创建了一个全新的盒子，并把 l1.val 复印了一份放进去。

空间： O ( n ) O(n) O(n)。如果你合并两个长度为 n n n 的链表，额外消耗了 2 n 2n 2n 的内存

---

假设原始链表是 [4, 2, 1, 3]：
第一阶段：向下拆分 (Divide)Level

1: sortList([4,2,1,3]) 启动。

• 快慢指针找到中点，pre.next = None 切断。
• 变成左边 [4,2] 和右边 [1,3]。

2: Level 2 (左): sortList([4,2]) 启动。

• 切断变成 [4] 和 [2]。

3: Level 3 (触底): sortList([4]) 和 sortList([2]) 启动。

• 触发递归出口（if not head.next），直接返回原节点。

第二阶段：向上合并 (Conquer)

1：合并 Level 3:

• merge([4], [2]) 执行，结果返回 [2,4]。

2：Level 2 (右): 同样的过程，sortList([1,3]) 拆分后合并，返回 [1,3]。

3：最终合并 Level 1

• merge([2,4], [1,3]) 执行。
• 最终返回 [1,2,3,4]

---

---

冒泡排序 （超出时间限制）

• 每次排列只能确定最大的，把最大的放结尾
• 循环。。
• 则最后从后往前，越来越小

为什么它叫"冒泡"？

就像水底的气泡一样，大的气泡会一直往上浮。

1. 第一轮循环：最大的数会像气泡一样，通过不断的交换，移动到链表的最末端。
2. 第二轮循环：次大的数会移动到倒数第二的位置。
3. 依此类推。

交换两个节点的值 (注意：不是交换节点本身

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:

        # 如果为空或只有一个节点，无需排序
        if not head or not head.next:
            return head   


        # 确定需要排序的边界
        end = None  
        # 只要没走到上一轮已经排好序的边界，就继续往后比

        while end != head.next:
            # 每次都从头开始，到上一轮末尾结束
            curr = head
            while curr.next != end:
                # 升序排列，大的放后面
                if curr.val > curr.next.val:
                    # 交换node1 node2  ，交换两个节点的值 (注意：不是交换节点本身)
                    curr.val, curr.next.val = curr.next.val, curr.val
                curr = curr.next

            # 每一轮走完，curr 会停在这一轮最大的数上
            # 下一轮就不用再比这个位置及以后的数了
            end = curr

        return head

不要写成交换节点！

只需要交换值

if node1.val > node2.val:
    # 交换开始！
    # 1. 让前驱节点指向 node2
    pre.next = node2
    
    # 2. 让 node1 指向 node2 的下一个（断开原来的连接）
    node1.next = node2.next
    
    # 3. 让 node2 指向 node1（完成位置互换）
    node2.next = node1
    
    # --- 关键的一步：修正指针状态 ---
    # 交换后，物理位置变了，但我们要让 node1 依然指向待比较的前者
    # 所以我们需要把 node1 和 node2 的名字"换回来"，或者通过 pre 重新定位
    node1, node2 = node2, node1