文章目录
剪枝,形象得看,就是剪掉搜索树的分支,从而减小搜索树的规模,排除掉搜索树中没有必要的分支,优化时间复杂度。
在深度优先遍历中,有几种常见的剪枝方法:1、排除等效冗余
如果在搜索过程中,通过某一个节点往下的若干分支中,存在最终结果等效的分支,那么就只需要搜索其中一条分支。
例如选数题目题目中的先选1再选2和先选2再选1,在组合中本质都是一种情况,需要剪掉。
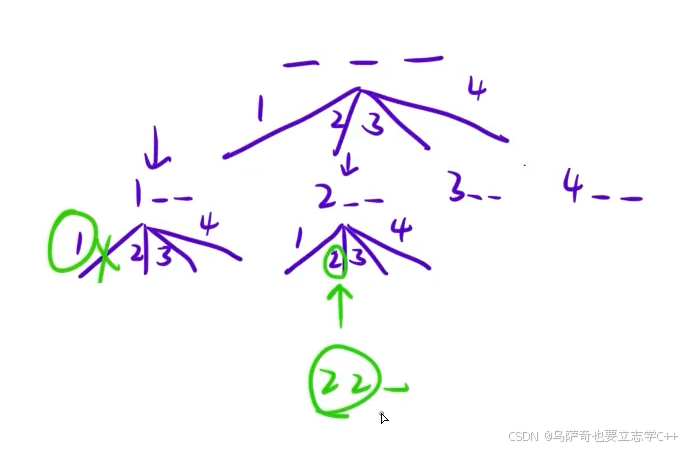
2、可行性剪枝
如果在搜索过程中,发现有一条分支是无论如何都拿不到最终解,此时就可以放弃这个分支,转而搜索其它的分支。
例如上一章的选数题目,本质就是组合,从m个数中选出n个,当某个分支选择两个相同的数就需要将该分支剪掉,因为此分支下面的分支都不可能是最终解。
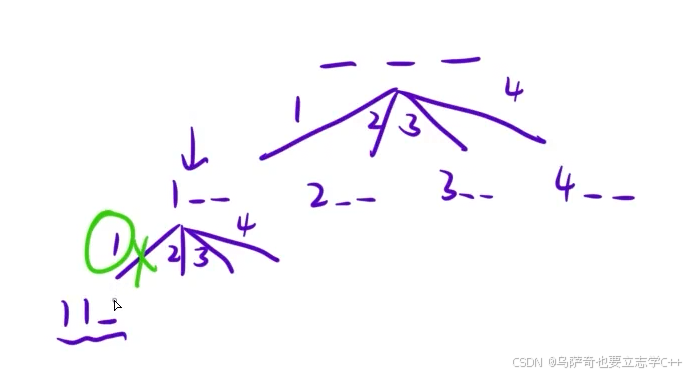
3、最优性剪枝
在最优化的问题中,如果在搜索过程中,发现某一个分支已经超过当前已经搜索过的最优解,那么这个分支往后的搜索,必定不会拿到最优解。此时应该停止搜索,转而搜索其它情况。
4、优化搜索顺序
在有些搜索问题中,搜索顺序是不影响最终结果的,此时搜索顺序的不同会影响搜索树的规模。
因此,应当先选择一个搜索分支规模较小的搜索顺序,快速拿到一个最优解之后,用最优性剪枝剪掉别的分支。
3、4两点一般用于最优化问题中,我们目前还没有遇到过。
5、记忆化搜索 用全局变量记录每一个状态的搜索结果,当下一次搜索到这个状态时,直接找到之前记录过的搜索结果。记忆化搜索,有时也叫动态规划。这类搜索问题都有典型特点,我们在下一节会细聊。
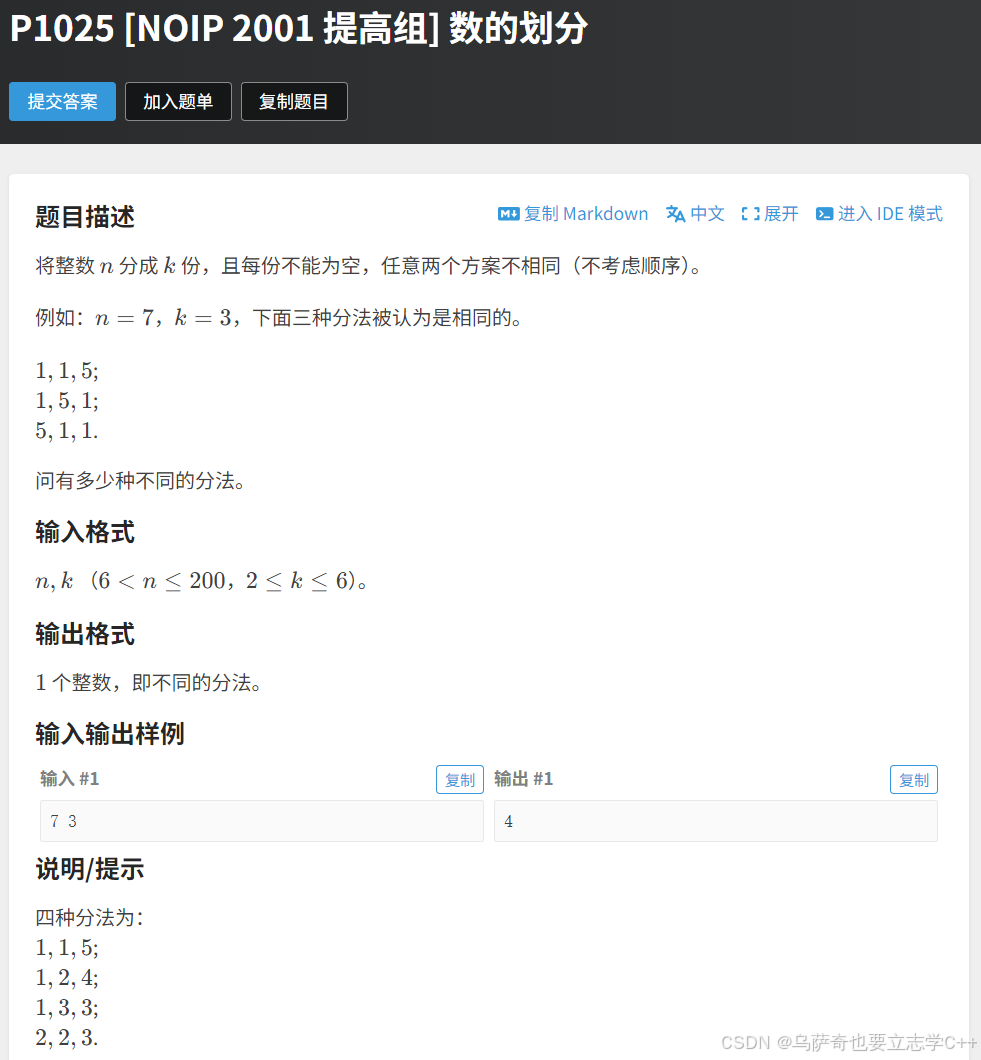
数的划分
题目描述
题目解析
本题整体思路和枚举组合类似,但本题由于数据较大,需要两种剪枝策略。
第一是排除等效冗余,例如先填1再填2和先填2再填1是同一种情况,需要剪掉,实现思路依旧dfs传递begin参数,但是本题在实际传参时应该传i,而不是枚举组合传递的i + 1,因为枚举组合题目是严格的组合,不能出现两个一模一样的数,但是本题可以出现两个一模一样的数,例如1 1 5。 第二是可行性剪枝,在dfs递归下一层时要先计算当前分支的最小值,然后和n比较,如果大于n说明此路径的最小情况都大于n,其他情况 只会大于等于n,所以需要直接剪掉。例如下图第一层中3往后所有情况都不满足,因为当第一个元素选3时最小情况都是3 3 3,结果为9大于7,所以for循环i枚举到3时可以判断后面3以及后面所有情况都不合法,直接剪掉。
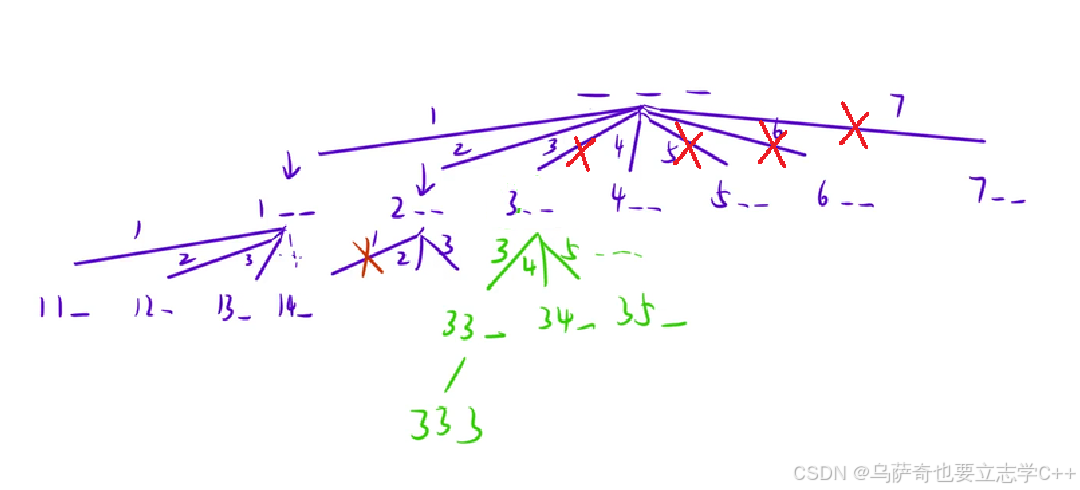
注意:
1、本题pos从0开始计数,因为这样k-pos就刚好是填到pos位置时还剩多少个格子没填,如果pos从1开始计数那么填到pos位置时还剩多少个格子没填就是k-pos+1。
2、本题思路整体和枚举组合一样,dfs要传两个参数pos(枚举哪个格子)和begin(这个格子从哪个数开始枚举),只不过这道题需要把多个相同的数也考虑进来,也就是原来多个相同的数是需要剪掉的,所以dfs是传递i+1,而本题应该传i。
代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int n, k;
int sum = 0; //当前选数方案的数之和
int ret; //统计有多少种分法
//pos表示填哪个格子,begin表示该格子枚举填数从哪个数开始
void dfs(int pos, int begin)
{
if (pos >= k)
{
if (sum == n)
ret++;
return;
}
for (int i = begin; i <= n; i++)
{
//dfs递归下一层之前就进行剪枝,会大大提升效率
if (sum + (k - pos) * i > n)
{
//可行性剪枝
//该子树的分支最小数目都比n大,该分支及以后的分支都不符合
return;
}
sum += i;
dfs(pos + 1, i); //注意这里第二个参数传i,而不应该传begin
sum -= i;
}
}
int main()
{
cin >> n >> k;
dfs(0, 1);
cout << ret << endl;
return 0;
}小猫爬山
题目描述
题目解析
本题我们还是先根据题意画出决策树:
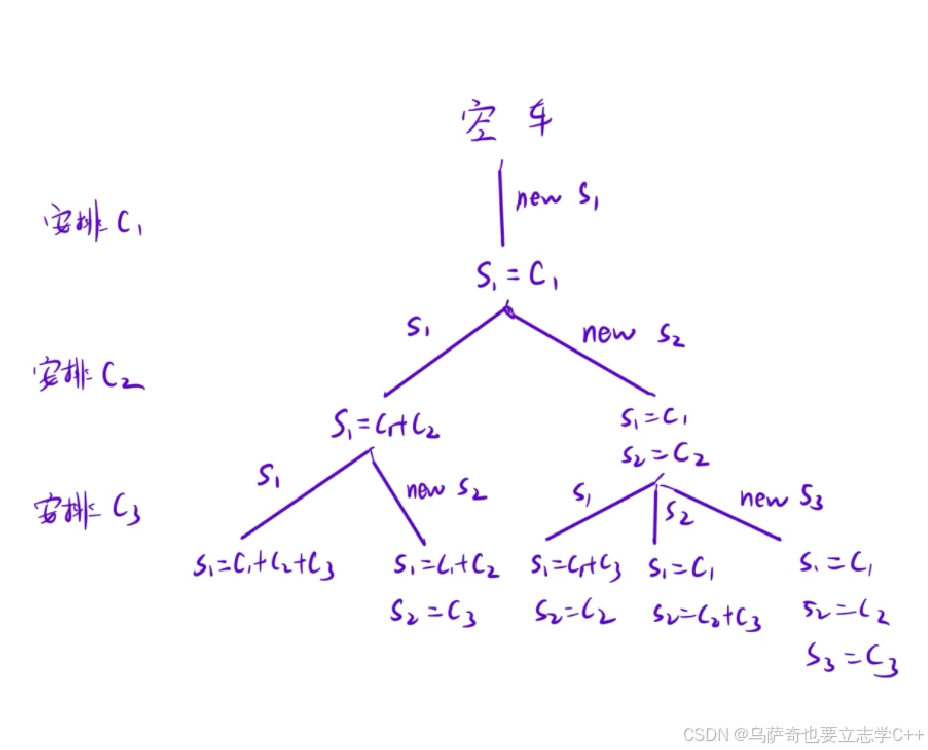
本质对于每一只猫就两种放法:放到已有的缆车中,或者重新开一辆缆车。但是本题的数据量比较大,所以需要进行剪枝,对于本题有三种剪枝策略:

一、可行性剪枝:
可行性剪枝用于将新猫放在依次放在已有的缆车中,若当新来的猫重量加上原本缆车中的猫重量大于w,就直接continue,判断下一辆缆车。
二、最优性剪枝:
当我们递归完一棵子树得到一个ret结果后,在递归其他子树时如果cnt已经等于ret了,说明继续往后递归可能得到的最好结果就是cnt,所以就可以将当前分支剪掉。
三、优化搜索顺序:
对于每只小猫的处理顺序是先放到已有的缆车中,再开新车,这样是为了贪心优先利用已有资源,尽早找到最优解,并且如果对于每只小猫都都先开新车的话,第一个得到的ret就是缆车数,也就是一车一猫,这个一定是最坏情况,这样就无法快速拿到尽量小的ret值进行后续分支的剪枝操作。
代码
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int n, w;
int cnt; //标记当前访问第几辆缆车,也就是当前用了多少辆缆车
int a[N]; //第i只小猫的重量
int st[N]; // 第i辆缆车的总重
int ret = N; //最少缆车数
bool cmp(int a, int b)
{
return a > b;
}
//pos表示第几只小猫
void dfs(int pos)
{
//策略一:最优性剪枝
if (cnt >= ret)
{
return;
}
if (pos > n)
{
//走到这里cnt一定比ret小,更新ret
ret = cnt;
return;
}
//策略三:优化搜索顺序
//先尝试放已有的缆车
for (int i = 1; i <= cnt; i++)
{
//策略一:可行性剪枝
if (a[pos] + st[i] > w)
continue;
st[i] += a[pos];
dfs(pos + 1);
st[i] -= a[pos];
}
//走到这里表示已有缆车不能放,需要开新车
cnt++;
st[cnt] += a[pos];
dfs(pos + 1);
st[cnt] -= a[pos];
cnt--;
}
int main()
{
//初始化数据
cin >> n >> w;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
//策略二:优化搜索顺序
sort(a + 1, a + 1 + n, cmp);
dfs(1);
cout << ret << endl;
return 0;
}以上就是小编分享的全部内容了,如果觉得不错还请留下免费的赞和收藏
如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
