数学定义用语法
eig 用来计算 矩阵的特征值 和 特征向量(Eigenvalues/Eigenvectors)。
cpp
eig 用来求特征值/特征向量,是 PCA、法向量估计、点云几何分析、ICP 的核心基础工具。
cpp
[V, D] = eig(A);
返回:
D:对角矩阵,包含特征值
V:每一列是一个特征向量
即:
A * V(:,i) ≈ D(i,i) * V(:,i)如果把矩阵 A 看成"变换",那么:
-
特征向量 = 变换后方向不变的向量
-
特征值 = 被放大的倍数
matlab 案例
例 1:对角矩阵
cpp
A = [3 0; 0 2];
[V,D] = eig(A)
V =
0 1
1 0
// V 是特征向量
D =
2 0
0 3
>>
//D 是特征值 例 1:非对角矩阵例子(旋转效果)
cpp
A = [2 1;
1 2];
[V,D] = eig(A)
V =
-0.7071 0.7071
0.7071 0.7071
D =
1 0
0 3、
解释:
λ = 3 方向被拉伸最大 → 主方向
λ = 1 对应最"弱"方向工程中的真实用途
PCA 求主方向(用 eig)
对协方差矩阵
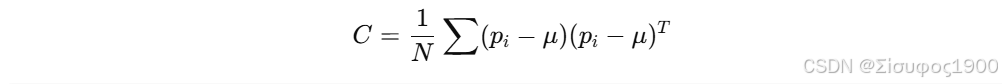
cpp
[V,D] = eig(C);
最大特征值 → 曲面主方向
最小特征值 → 法向量
所有点云法向量算法都用 eig点云平面拟合(法向量 = 最小特征值方向)
cpp
normal = V(:,1); % 最小特征值对应这是 PCL / Open3D / MATLAB 同一种逻辑
ICP 求解 SVD/EIG(旋转矩阵)
如果你不用 svd,你可以:
 NDT、GICP 的协方差分析
NDT、GICP 的协方差分析
特征值代表局部点云"扁平程度":
-
λ₁ ≪ λ₂, λ₃ → 非常平(地面)
-
λ₁ ≈ λ₂ ≈ λ₃ → 球状噪声
-
λ₁ ≪ λ₂ ≈ λ₃ → 线
GICP/NDT 就是用这些性质约束优化。
eig 和 svd 在 PCA 中的区别
PCA 本质在求什么?
PCA 要求:
-
主方向(Eigenvectors)
-
主方差大小(Eigenvalues)
等价于:
-
对协方差矩阵做 特征分解(eig)
-
或者对数据矩阵直接做 奇异值分解(svd)
两者结果 完全一致(只差符号与排序)。
eig 和 svd 的区别总结表
| 项目 | eig | svd |
|---|---|---|
| 输入 | 协方差矩阵 C | 原始数据矩阵 X |
| 要求 | C 必须对称 | X 任意矩阵都行 |
| 输出 | PCA 特征值、方向 | PCA 特征值(σ²)和方向(U) |
| 稳定性 | 稳定,但需要先算 C | 最稳定(强烈推荐) |
| 数据量很大时 | C 是 d×d,小 | X 是 N×d,可能巨大 |
| 工程实际使用 | 仅在维度低时用 | 深度学习、点云、视觉都用 SVD |
数据量大时 → 用 SVD
维度小(3×3、6×6)时 → eig 足够快
数学关系
eig

svd

MATLAB 示例对比:
cpp
% 1. 构造 2D 数据(一个斜方向拉伸的高斯)
rng(0);
theta = pi/6;
R = [cos(theta) -sin(theta); sin(theta) cos(theta)];
D = [3 0; 0 1]; % 方差不同
X = randn(1000,2) * D * R'; % N×2
Xc = X - mean(X); % 去中心化
%% === 方法1:eig ===
C = cov(Xc); % 协方差矩阵
[V_eig, D_eig] = eig(C);
%% === 方法2:svd ===
[U,S,V_svd] = svd(Xc,'econ');
% SVD 得到的特征值(注意平方/N)
lambda_svd = diag(S).^2 / size(X,1);
%% 比较
V_eig
V_svd
lambda_svd
diag(D_eig)
结论:
eig 是对协方差矩阵做特征分解;
svd 是对数据矩阵做奇异值分解。
svd 更稳定且适合大规模数据,
eig 只适合小规模(如 3×3)几何问题。