大学院-筆記試験練習:线性代数和数据结构(21)
- 1-前言
- 2-线性代数-题目
- 3-线性代数-参考答案
- 4-数据结构-题目
-
- [在这里插入图片描述 ](#在这里插入图片描述
 )
)
- [在这里插入图片描述 ](#在这里插入图片描述
- 【問1】二分探索木
- 【問2】探索アルゴリズム(BFS)
- 【問3】ソートアルゴリズム(空欄補充)
- 5-数据结构-参考答案
- 【問題1】ヒープと優先度付きキュー【解答】
- 【問題2】ハッシュ法と衝突処理【解答】
- 【問題3】Union-Find(素集合データ構造)【解答】
- 【問題4】動的配列と償却計算量【解答】
- 6-总结
1-前言
为了升到自己目标的大学院,所作的努力和学习,这里是线性代数和数据结构部分。
2-线性代数-题目

【相似题①】(一次独立・一次従属)
以下の問いにすべて答えよ。計算の途中経過も記載すること。
\\text{次のベクトルの組} \\quad \\left{ \\begin{pmatrix}1\\2\\3\\end{pmatrix}, \\begin{pmatrix}2\\4\\6\\end{pmatrix}, \\begin{pmatrix}1\\0\\1\\end{pmatrix} \\right}
が一次独立であるか,一次従属であるかを判定せよ。
また,一次従属である場合には,その一次関係式を1つ求めよ。
🔎 出题意图(你心里要懂)
- 看你会不会立刻发现「倍数关系」
- 但第三个向量会干扰判断(立命馆常见)
【相似题②】(点と平面・垂線・距離)
以下の問いにすべて答えよ。計算の途中経過も記載すること。
点 (A(2,-1,4)) と
平面 (\pi: 2x-y+z-5=0) が与えられている。
(1) 点 (A) を通り,平面 (\pi) に垂直な直線の方程式を求めよ。
(2) その直線と平面 (\pi) との交点を § とするとき,点 § の座標を求めよ。
(3) 線分 (AP) の長さを求めよ。
🔎 出题意图
- 法線ベクトルの即時判定
- 代入計算での符号ミス誘発
- 距離公式を"丸暗記してるか"チェック
3-线性代数-参考答案



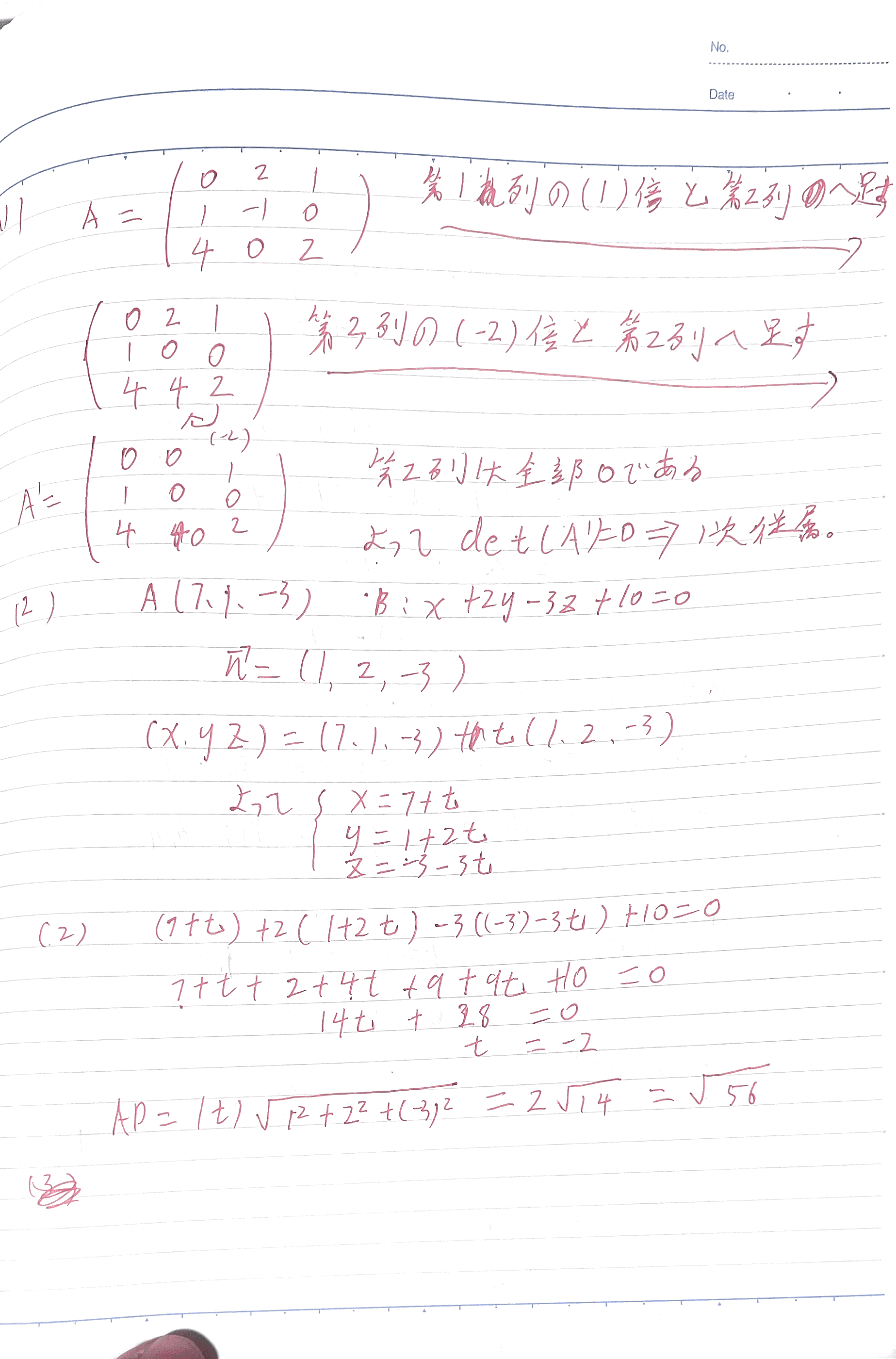
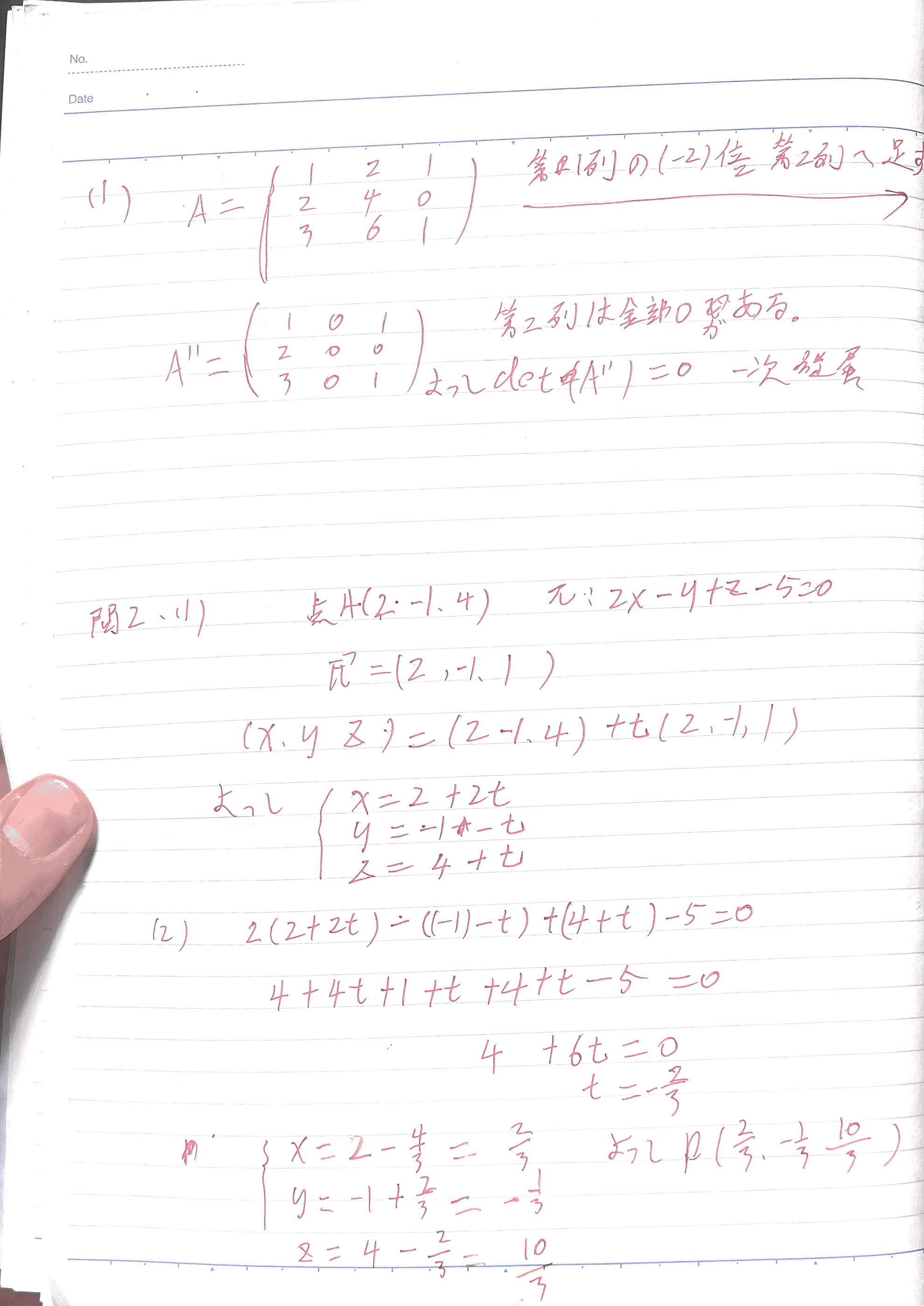

4-数据结构-题目

【問1】二分探索木
(1)
数列
S={3,7,1,5}
を先頭から順に挿入すると,得られる二分探索木は次のとおりである。
3
/ \
1 7
/
5(2)
visit 関数は
節点 → 左部分木 → 右部分木
の順で訪問する(先行順探索)。
したがって表示される値の順序は次のとおりである。
3,\\ 1,\\ 7,\\ 5
(3)
挿入される数列が昇順に整列されている場合,
二分探索木は片側にのみ伸び,高さが (n) となる。
よって insert 関数全体の最悪時間計算量は
O(n\^2)
である。
(4)
図2の二分探索木の根に対して右に単回転を行うと,
得られる木構造は次のとおりである。
3
/ \
2 5
/ / \
1 4 6【問2】探索アルゴリズム(BFS)
(1)
グラフを隣接行列で実現した場合,
2 つの頂点が隣接しているかの判定に要する時間計算量は
O(1)
である。
(2)
グラフを隣接リストで実現した場合の空間計算量は
O(n+m)
である。
(3)
頂点 1 を始点として BFS を行うと,
訪問される頂点の順序は次のとおりである。
1,\\ 2,\\ 4,\\ 6,\\ 3,\\ 5
(隣接頂点は頂点番号の昇順で処理する)
(4)
BFS においてキュー Q に格納される要素数の最大値は,
頂点数 (n) に比例するため,
O(n)
である。
(5)
キューを用いる処理をスタックに変更すればよい。
【問3】ソートアルゴリズム(空欄補充)
(1) 計数ソート
(2) 最小値
(3) (O(n^2))
(4) 比較
(5) (O(n\log n))
(6) (O(n\log n))
(7) ピボット
(8) (O(n\log n))
(9) (O(n^2))
(10) 安定
【問題1】ヒープと優先度付きキュー(模拟)
最大ヒープを用いて優先度付きキューを実装する。
ヒープは完全二分木として配列で表現され,
配列の先頭要素の添字を 1 とする。
(1)
要素数 (n) の最大ヒープに対して,新たな要素を 1 つ挿入する操作の時間計算量を,
オーダー表記で答えよ。
(2)
最大ヒープから最大要素を削除する際の処理手順を,
ヒープ条件の回復方法に着目して簡潔に説明せよ。
(3)
ヒープソートが安定なソートでない理由 を,
同じ値をもつ要素の順序に着目して説明せよ。
【問題2】ハッシュ法と衝突処理(模拟)
要素数 (n) の集合を管理するためにハッシュ表を用いる。
衝突解決法として**オープンアドレス法(線形探索)**を採用するものとする。
(1)
ハッシュ表における**負荷率(ロードファクタ)**を定義せよ。
(2)
負荷率が高くなると探索時間が増加する理由を説明せよ。
(3)
線形探索法において,
削除操作を単純に行うと問題が生じる理由を述べよ。
(4)
(3) の問題を解決するために一般に用いられる方法を 1 つ挙げ,
その概要を説明せよ。
【問題3】Union-Find(素集合データ構造)(预测)
要素数 (n) の集合に対して,Union-Find(素集合データ構造)を用いる。
(1)
Union 操作および Find 操作の役割をそれぞれ簡潔に説明せよ。
(2)
経路圧縮を用いることで Find 操作が高速化される理由を述べよ。
(3)
Union-by-rank(または Union-by-size)を用いる目的を説明せよ。
(4)
経路圧縮と Union-by-rank を併用した場合の,一連の操作に対する
償却計算量について述べよ。
【問題4】動的配列と償却計算量(预测)
要素を末尾に追加できる動的配列を考える。
配列が満杯になった場合には,
容量を 2 倍に拡張し,全要素を新しい配列にコピーするものとする。
(1)
要素を 1 つ追加する操作の最悪時間計算量を答えよ。
(2)
同じ操作の償却時間計算量を答えよ。
(3)
(2) のように評価できる理由を,
要素のコピー回数と操作回数の関係に着目して説明せよ。
5-数据结构-参考答案


【問題1】ヒープと優先度付きキュー【解答】
(1)
最大ヒープへの要素 1 つの挿入は,上方向への調整が高々木の高さ分で済むため,
O(\\log n)
である。
(2)
根(最大要素)を削除し,末尾要素を根に移動させた後,
左右の子と比較しながらヒープ条件を満たすまで下方向に交換して調整する(down-heap / sift-down)。
(3)
ヒープソートでは,ヒープ化や調整の過程で要素の交換が発生し,
同じ値をもつ要素の相対的な順序が保持されない可能性があるため,安定ではない。
【問題2】ハッシュ法と衝突処理【解答】
(1)
負荷率(ロードファクタ)とは,
格納されている要素数をハッシュ表の大きさで割った値である。
(2)
負荷率が高くなると衝突が増加し,
探索時に複数の位置を順に調べる必要が生じるため,探索時間が増加する。
(3)
線形探索法では,削除した要素を単に空にすると探索が途中で終了し,
削除位置の後方にある要素が探索できなくなる場合がある。
(4)
削除済みを示す特別な印(削除マーク,tombstone)を用いる。
探索では削除マークを空とはみなさず探索を継続し,挿入では削除マークの位置を再利用する。
【問題3】Union-Find(素集合データ構造)【解答】
(1)
Union 操作は 2 つの集合を 1 つに統合する操作である。
Find 操作は要素が属する集合の代表元を求める操作である。
(2)
Find の際に通過した節点を直接代表元に接続することで木の高さが低くなり,
後続の Find が高速化される。
(3)
高さ(または要素数)の小さい木を大きい木の下に接続することで,
木が過度に深くなるのを防ぐことを目的とする。
(4)
経路圧縮と Union-by-rank を併用した場合,
一連の Union / Find 操作の償却計算量はほぼ定数時間であり,
厳密には逆アッカーマン関数 (\alpha(n)) に比例する。
【問題4】動的配列と償却計算量【解答】
(1)
満杯時には全要素のコピーが必要となるため,最悪時間計算量は
O(n)
である。
(2)
同じ操作の償却時間計算量は
O(1)
である。
(3)
拡張は容量が倍増するタイミングでのみ発生し,
各要素がコピーされる回数は全体で高々定数回に抑えられる。
したがって,操作全体で平均すると 1 回あたりの計算量は定数時間として評価できる。
6-总结
训练成长。!!
