1 DFT/FFT
DFT (离散傅里叶变换)
它的本质就是之前相关性极致应用。拿一堆不同频率的正弦波去跟被测信号算"乘积和"。哪个频率算出来的数大,就说明信号里含有哪个频率成分。
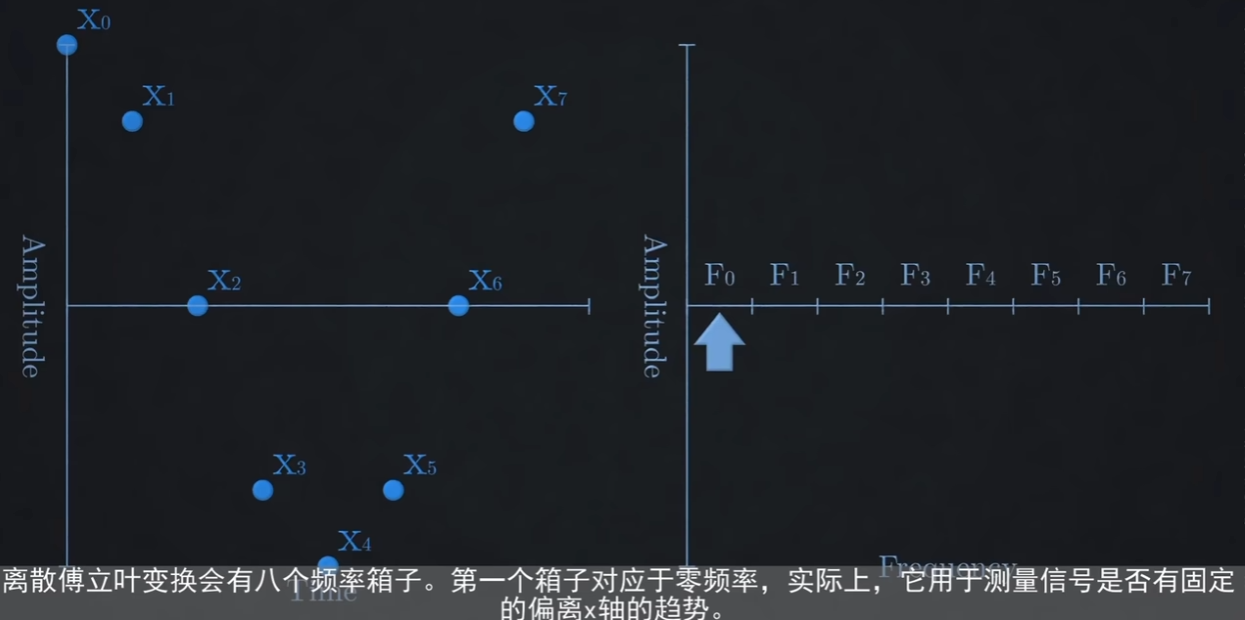
DFT的算法还是能理解,不算太困难。比如下面这个,左边有8个点,然后右边有8个比较的频率。每个X点乘以F点,求和算出那个频率的能量最大。这个算法的本身没问题,就是运算量大,时间是N的平方。
FFT (快速傅里叶变换)
DFT 的计算量是 N^2,如果信号长,计算量就太大,电脑就跑不动了。
FFT 利用了正弦波的对称性,比如依然是上面8个点的示意图,所有要计算的波叠加在一起,可以看到圈出来的点一共计算了8次,但是这8次只有2次是独立的,而其余的6次都是重复计算,所以计算2次其实就够了。这种总共把8个点算完,计算24次就够了,不是DFT的64次。在数据量越大,这个运算差距更明显。
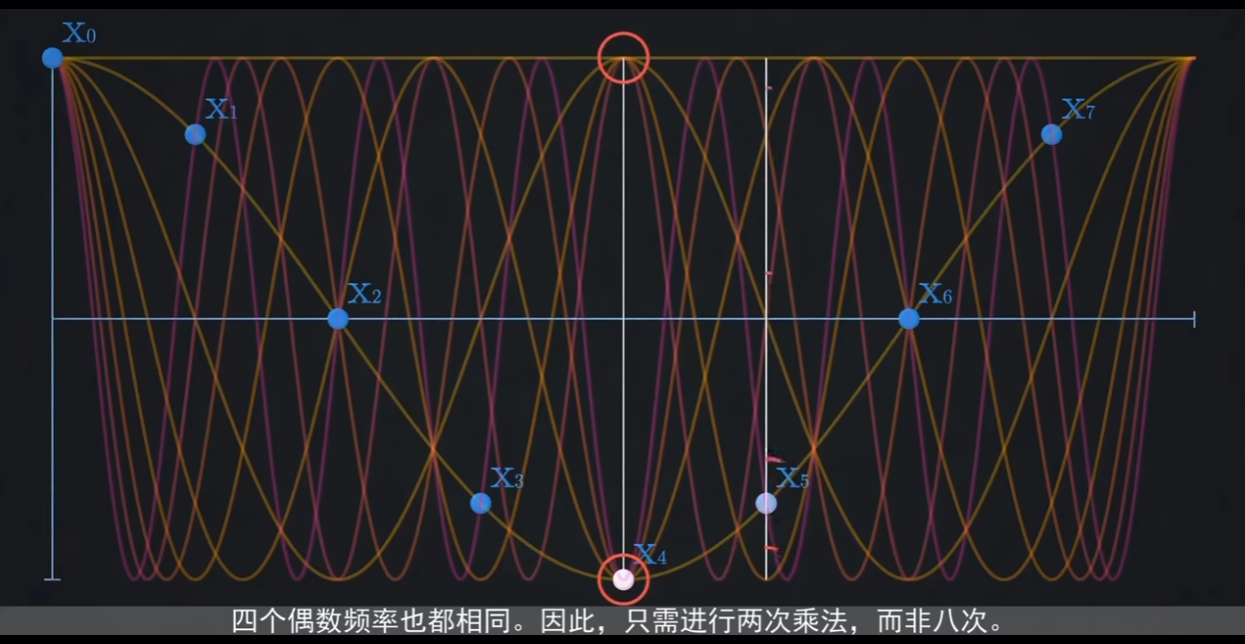
简单看了一下算法,其实FFT就是一个递归。把计算量降到了 Nlog2N。这直接让实时信号处理变成了可能(比如你的手机能实时显示均衡器跳动)。

实验:
python
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 参数设置 ---
fs = 1000 # 采样率 (Hz)
N = 1000 # 采样点数
t = np.linspace(0, 1, N, endpoint=False) # 时间轴
# --- 2. 构造信号 ---
# 50Hz 主信号 + 一些噪声
clean_signal = np.sin(2 * np.pi * 50 * t)
noise = 0.8 * np.random.randn(N)
signal = clean_signal + noise
# --- 3. 执行 FFT ---
fft_result = np.fft.fft(signal)
amplitudes = np.abs(fft_result) / (N / 2) # 归一化振幅
frequencies = np.fft.fftfreq(N, 1/fs)
# --- 4. 绘图 (上下两部分) ---
plt.figure(figsize=(10, 8))
# 上半部分:时域波形 (Time Domain)
plt.subplot(2, 1, 1) # 2行1列,第1张
plt.plot(t[:200], signal[:200]) # 只画前200个点,看得更清楚
plt.title("Time Domain: Signal + Noise")
plt.xlabel("Time (s)")
plt.ylabel("Amplitude")
plt.grid(True)
# 下半部分:频域结果 (Frequency Domain)
plt.subplot(2, 1, 2) # 2行1列,第2张
# 只画正频率部分 (0 到 fs/2)
plt.plot(frequencies[:N//2], amplitudes[:N//2], color='red')
plt.title("Frequency Domain: FFT Result")
plt.xlabel("Frequency (Hz)")
plt.ylabel("Amplitude")
plt.grid(True)
plt.tight_layout() # 自动调整布局,防止标题重叠
plt.show()结果
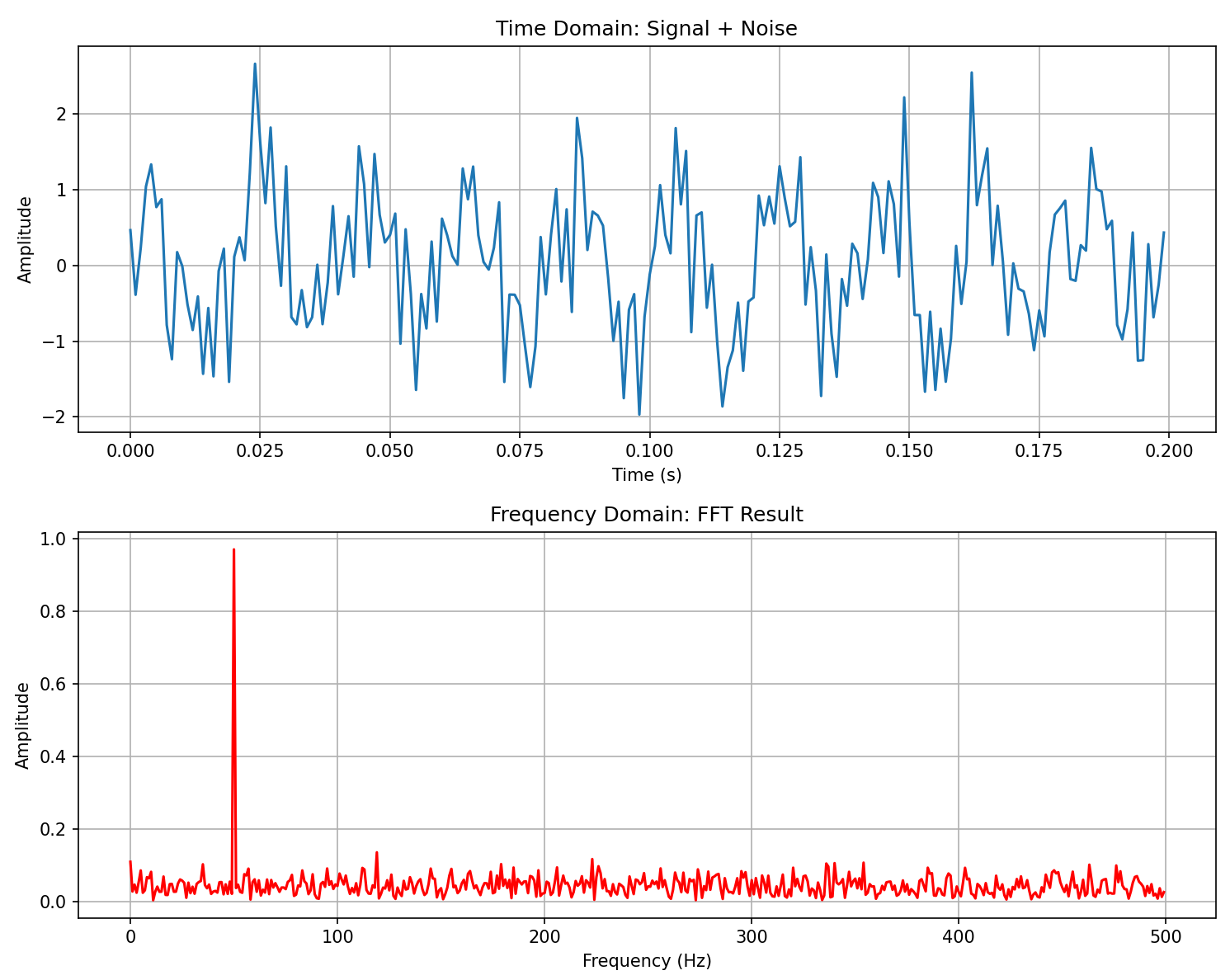
2 频谱泄露
FFT 默认你截取的那段信号是周期循环的。但如果截取的位置正好不在波形的周期点上(首尾接不起来),在 FFT 看来,信号就在边缘处发生了一个剧烈的跳变。在微积分和傅里叶变换理论中,一个瞬时的跳变(类似于阶跃信号)包含了无限宽的频谱。为了用一堆平滑的正弦波去"凑"出这个生硬的跳变点,FFT 必须在结果中加入大量的其他频率成分。
比如输入的是一个纯净的 50Hz 正弦波,FFT 出来的结果却在 50Hz 周围有一堆乱七八糟的小毛刺。
具体的试验在下个部分做。
3 窗函数
给信号乘一个"中间高、两头低"的函数(比如 汉宁窗 Hanning 或 海明窗 Hamming)。强制让信号在这一帧的开头和结尾逐渐归零。这样首尾相连时就平滑了,泄露也就被极大地抑制了。但是窗函数会把频谱的峰值"变胖"(分辨率下降)。
比起FFT,窗函数就简单多了。下面是最常用的汉明窗 (Hamming Window)。
公式:
-
n:当前采样点的序号。
-
N:总的采样点数(窗口长度)。
实现代码:
cpp
#include <math.h>
#define WINDOW_SIZE 512
float hamming_table[WINDOW_SIZE];
// 1. 初始化:预先算好窗函数表(在系统启动时运行一次)
void init_hamming_window() {
for (int n = 0; n < WINDOW_SIZE; n++) {
hamming_table[n] = 0.54f - 0.46f * cosf(2.0f * M_PI * n / (WINDOW_SIZE - 1));
}
}
// 2. 处理:将原始信号和窗函数相乘
void apply_window(float *input_signal, float *output_signal) {
for (int i = 0; i < WINDOW_SIZE; i++) {
// 每个采样点乘以对应的窗系数
output_signal[i] = input_signal[i] * hamming_table[i];
}
}不同的窗函数应用:
| 窗函数名称 | 特点 | 适用场景 |
|---|---|---|
| 矩形窗 (Rectangular) | 边缘直接切断 | 只有当你处理的信号周期刚好和采样长度对齐时才用。 |
| 汉明窗 (Hamming) | 边缘平滑,性能均衡 | 最通用。语音识别、普通频谱分析。 |
| 汉宁窗 (Hann) | 边缘完全降到 0 | 适合对频率精度要求高的情况。 |
| 布莱克曼窗 (Blackman) | 泄露极低,但主峰很宽 | 适合寻找强信号旁边隐藏的微弱小信号。 |
使用窗函数的前后对比。
python
import numpy as np
import matplotlib.pyplot as plt
# 1. 信号设置
fs = 1000
N = 200
t = np.arange(N) / fs
freq = 123.4
clean_x = np.sin(2 * np.pi * freq * t)
noise = 0.2 * np.random.randn(N)
x = clean_x + noise
# 2. 方案 A: 仅加窗
window = np.hamming(N)
x_windowed = x * window
# 3. 方案 B: 差分方程 (滑动平均) + 加窗
# 我们用一个 5 点滑动平均滤波器:y[n] = (x[n] + x[n-1] + ... + x[n-4]) / 5
def moving_average(data, window_size=5):
return np.convolve(data, np.ones(window_size)/window_size, mode='same')
x_avg = moving_average(x, window_size=5)
x_avg_windowed = x_avg * window
# 4. 计算 FFT
def get_fft_db(sig):
mag = np.abs(np.fft.rfft(sig))
return 20 * np.log10(mag + 1e-6)
freqs = np.fft.rfftfreq(N, 1/fs)
fft_raw = get_fft_db(x)
fft_win = get_fft_db(x_windowed)
fft_combo = get_fft_db(x_avg_windowed)
# 5. 绘图
plt.figure(figsize=(12, 8))
plt.subplot(2, 1, 1)
plt.plot(t, x, 'gray', alpha=0.5, label='Raw Noisy')
plt.plot(t, x_avg, 'b', label='After Moving Average (Time Domain)')
plt.title("Time Domain: Smoothing the Spikes")
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(freqs, fft_raw, 'r', alpha=0.5, label='Raw + No Window')
plt.plot(freqs, fft_win, 'g', label='Raw + Hamming Window')
plt.plot(freqs, fft_combo, 'b', lw=2, label='MovingAvg + Hamming (The Combo)')
plt.axvline(freq, color='k', linestyle='--', label='Target Freq')
plt.ylim(-20, 40)
plt.title("Frequency Domain: The 'Combo' approach cleans the floor")
plt.legend()
plt.tight_layout()
plt.show()结果
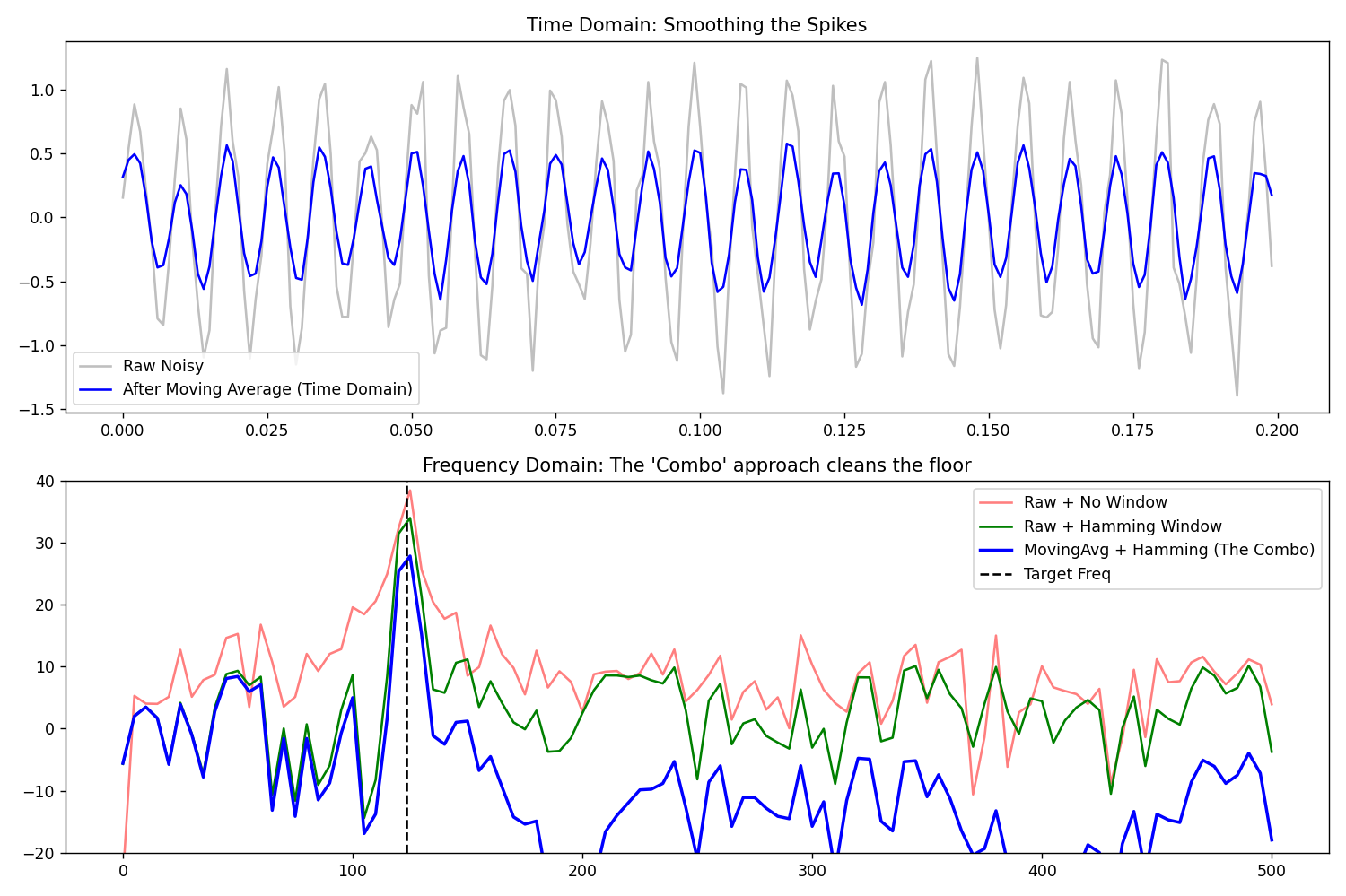
可以看到,在多重算法下首先是降低了底噪,然后真实频率更加突出。
4 DCT
FFT 是基于圆周旋转的(复数,有实部虚部);DCT 只用余弦波,只处理实数。相比 FFT,DCT 能把信号大部分的能量压缩到极少数的几个低频系数上。
这里的高低频,不是颜色的频率,而是变化的频率,就是数值的变化。低频就是变化不剧烈,高频就是变化剧烈。
目前看到的JPG图片和听到的MP3音乐,核心压缩算法全是DCT。因为它能用最少的数据量还原出人眼/人耳最关心的特征。人眼对亮度的敏感程度,是高于对颜色的敏感程度。
也就是说以前我们看黑白电视,或者黑白视频,也可以看的很欢乐的原因。对于人眼的这种特征,所以有了YUV格式,其中Y就是亮度,如果是黑白,那么只要亮度就行了。在YUV中,UV蓝红是颜色,人眼不敏感,直接大幅度压缩,从采样开始就去掉75%。然后只保留一些低频信号。对于Y亮度,保留低频的部分,一般高频的部分直接压缩取0,特别高频的就是轮廓然后保留。
DCT相对FFT只用了余弦,然后对数据做镜像扩展。。。也不去计算相位。。。
好了,暂时先写到这里吧,图形的处理感觉还有很多要看的,比如图形频率的准确定义。后面再弄吧。。。