0 引言
心血管疾病（cardiovascular diseases, CVD）危险因素对居民健康的影响日益凸显，其发病率呈持续攀升态势。CVD 所带来的社会与经济负担不断加重，已成为全球性重大公共卫生问题，位列危害人类健康的三大主要疾病之一，患病率与死亡率均居全球首位。在中国，CVD 患病率同样处于持续上升阶段，推算现患人数达 3.3 亿，其中脑卒中 1300 万、冠心病 1139 万、心力衰竭 890 万、肺源性心脏病 500 万、心房颤动 487 万、风湿性心脏病 250 万、先天性心脏病 200 万、外周动脉疾病 4530 万、高血压 2.45 亿 [1]。动脉硬化是 CVD 的核心病理基础之一，研究证实，动脉硬化的早期特征性表现为血管壁内中膜增厚，进而引发动脉壁弹性下降。血管壁二维运动的精准检测是评估血管弹性的关键前提，因此，实现血管壁二维运动的有效检测，可为血管弹性评估提供可靠依据，对 CVD 的早期筛查与诊断具有重要临床价值 [2]。
在第一个工作中，我们以超声图像纵向运动场景为对象，先探究了块匹配算法的基本原理，基于 MATLAB 实现了 NCC、MAD、MSD 三种匹配准则下的像素级运动检测，并对比分析了三种匹配准则下的运动检测结果差异[]。由于第一个工作上述结果所得结果均为像素级精度，难以满足精细的位移分析需求，所以在第二个工作中在上述匹配准则的基础上，引入二次函数插值算法进行优化，进而实现了亚像素级径向位移的精准求解，并基于 MATLAB 平台完成了该优化算法的实现与验证[]。虽然是插值优化虽提升了位移精度，但对超声图像中因噪声、纹理不均导致的运动轨迹波动缺乏有效的平滑处理，难以满足高精度、高鲁棒性的运动分析需求。为此，本工作进一步拓展研究维度，提出一种融合 SG（Savitzky-Golay）滤波的超声图像运动分析方法，以实现超声图像运动特征的更精准提取。
目录
[0 引言](#0 引言)
[1 SG滤波理论](#1 SG滤波理论)
[2 基于SG滤波的径向位移的估计](#2 基于SG滤波的径向位移的估计)
[3 结果分析](#3 结果分析)
[4 讨论](#4 讨论)
[5 参考](#5 参考)
1 SG滤波理论
Savitzky-Golay滤波器由Abraham Savitzky和Marcel J. E. Golay于1964年提出，是一种应用广泛的数字滤波器，可用于数据平滑和微分运算。与传统的中值滤波或均值滤波等容易造成信号特征损失的方法相比，Savitzky-Golay滤波器能够在实现信号平滑的同时保持原始信号的关键特征。 这一特性使其在信号形状和特征保持要求较高的应用场景中具有显著优势。 Savitzky-Golay滤波器是一种基于局部多项式回归的数字滤波器，其核心是通过线性最小二乘法将低阶多项式拟合到相邻数据点的滑动窗口中。该方法的主要优势在于能够在降低噪声的同时保持信号的高阶矩，这意味着信号的峰值、谷值等特征可以得到较好的保持[5-6]。因此，广泛应用于超声图像纵向运动的估计当中[7-9]
这里我们将简单阐述SG滤波理论的原理部分，以便后续理解。设离散信号为：
对第 k 个点，取窗口长度 L=2m+1（奇数），窗口内信号：
窗口内用 p 阶多项式拟合：
其中 t=−m,−m+1,...,0,...,m−1,m 为中心化窗口坐标 。最终目标是求系数，使残差平方和最小：
同线性回归一致，采用最小二乘法求解系数：
其中，，
，
为：
即解为：，其中
的大小为L× (p+1);
的大小为 (p+1)×L。滤波后输出为中心拟合值：
， 其中
为 SG 卷积核（权重）：
的第一行给出。从上述推导可以看出：需要调节的参数仅有p（阶数）和m（窗口）。因此，合适的阶数和窗口数影响着滤波效果。 这里基于Python举个例子进行可视化展示，代码如下：
python
import numpy as np
from scipy.linalg import inv
from scipy.signal import savgol_filter
import matplotlib.pyplot as plt
def calc_sg_weights(window_length, poly_order):
"""
手动计算SG滤波权重（核心：取(X^TX)^-1X^T的第0行做平滑，第1行做一阶导数）
:param window_length: 窗口长度（必须奇数）
:param poly_order: 多项式阶数（< window_length）
:return: smooth_weights: 平滑权重（第0行）, deriv1_weights: 一阶导数权重（第1行）
"""
# 1. 生成中心化窗口坐标（-m, -m+1, ..., 0, ..., m-1, m）
m = (window_length - 1) // 2
t = np.arange(-m, m + 1)
# 2. 构建范德蒙德矩阵 X (L × (p+1))
X = np.vander(t, poly_order + 1, increasing=True)
# 3. 计算 W = (X^T X)^-1 X^T （核心矩阵）
X_T = X.T
W = inv(X_T @ X) @ X_T
# 4. 提取权重：第0行=平滑权重，第1行=一阶导数权重
smooth_weights = W[0, :] # 重点：平滑权重选第0行
return smooth_weights
window_length = 5
poly_order = 2
# 手动计算权重
smooth_w = calc_sg_weights(window_length, poly_order)
np.random.seed(42)
x = np.linspace(0, 4*np.pi, 100)
y_clean = np.sin(x) + 0.5 * np.cos(2*x) # 原始信号
y_noisy = y_clean + np.random.normal(0, 0.2, len(x)) # 加噪声
# 手动卷积实现SG平滑（用第0行权重）
y_smooth_manual = np.convolve(y_noisy, smooth_w, mode='same')
# 对比scipy官方SG滤波（验证手动计算正确性）
y_smooth_scipy = savgol_filter(y_noisy, window_length, poly_order)
#可视化结果
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文显示
plt.figure(figsize=(12, 8))
plt.plot(x, y_noisy, 'gray', alpha=0.5, label='带噪声信号')
plt.plot(x, y_clean, 'k--', label='原始无噪信号')
plt.plot(x, y_smooth_manual, 'r-', linewidth=2, label='手动SG平滑（第0行权重）')
plt.plot(x, y_smooth_scipy, 'b:', linewidth=2, label='scipy SG平滑')
plt.title(f'SG滤波平滑效果（窗口={window_length}, 阶数={poly_order}）')
plt.legend()
plt.grid(True, alpha=0.3)从图1中可以看出，在多项式阶数 p=2 固定的情况下，窗口长度 m 的选择对 SG 滤波效果有显著影响：当 m=5（窗口长度 L=5）时，滤波曲线既能有效抑制噪声，又能较好地保留原始信号的细节，手动实现与 scipy.savgol_filter 的结果几乎完全重合，验证了权重选取的正确性；而当 m=13（窗口长度 L=13）时，虽然噪声被大幅压制，曲线变得更加平滑，但信号的快速变化特征被明显 "抹平"，出现了过平滑现象，导致与原始无噪信号的偏差增大，不过手动实现与官方实现依然高度一致，说明权重计算逻辑在大窗口下依然稳定可靠。
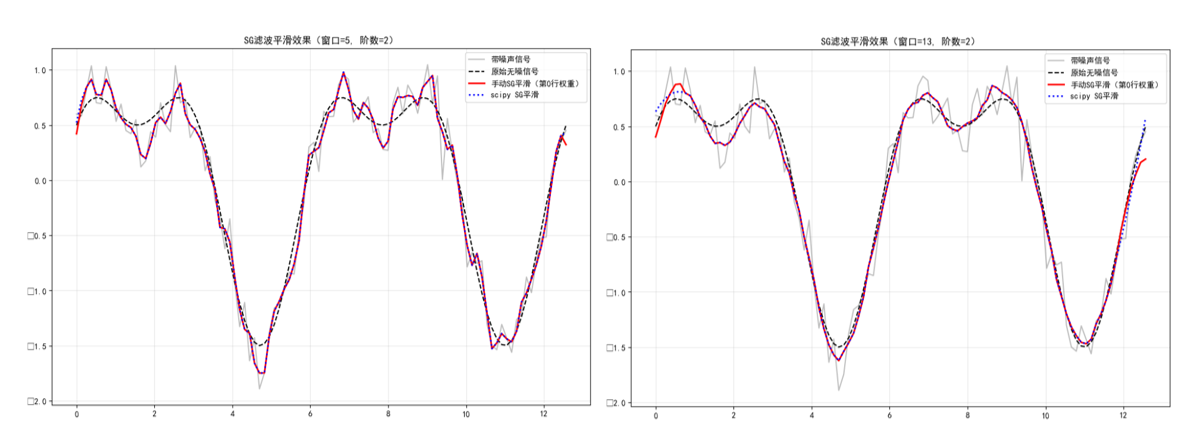图1 Savitzky-Golay滤波例子展示
2 基于SG滤波的径向位移的估计
在第二个工作中，我们已基于归一化互相关（NCC）、平均绝对差（MAD）和均方差（MSD）三种匹配规则，实现了亚像素级径向位移估计。为进一步提升位移测量的鲁棒性与精度，研究引入 Savitzky‑Golay（SG）滤波对位移序列进行预处理，并通过设置不同窗口长度与多项式阶数的组合，系统分析滤波参数对测量结果的影响。最终，以人工标注的真实位移值为参考，采用均方根误差（RMSE）作为定量评价指标（见下面公式），对各参数组合下的测量精度进行了全面评估与对比。
第二个工作中径向位移估计代码如下（MATLB）：
Matlab
clc;
clear;
% 启动计时器
tic;
load("B1.mat");
num_frames = size(new_data, 3);
r = zeros(1,num_frames);
c = zeros(1, num_frames);
% 确定参考帧和匹配帧的尺寸大小
%参考帧：cw起始行a 终点行b 起始列d 终点列e
%匹配帧：cw1起始行a1 终点行b1 起始列d1 终点列e
p=10;%最大像素位移
a=321;
b=330;
d=41;
e=50;
a1=a-p;b1=b+p;d1=d-p;e1=e+p;
for k = 1:num_frames
cw = new_data(a:b, d:e, 1);%参考帧
cw_t = new_data(a1:b1, d1:e1, k);%匹配帧
R = zeros(2*p+1, 2*p+1);
% 计算相关系数矩阵
for i = 0:2*p
for j = 0:2*p
%R(i+1,j+1) = calc_corr(cw_t(i+1:i+10,j+1:j+10), cw);
%R(i+1,j+1) = calc_mad(cw_t(i+1:i+10,j+1:j+10), cw);
R(i+1,j+1) = calc_msd(cw_t(i+1:i+10,j+1:j+10), cw);
end
end
[sorted_values, sorted_indices] = sort(R(:), 'descend');
[rows, cols] = ind2sub(size(R), sorted_indices);
found = false;
for idx = 1:length(sorted_values)
current_row = rows(idx);
current_col = cols(idx);
if k == 1
row_indices = current_row;
col_indices = current_col;
found = true;
break;
end
current_dist = current_row - r(k-1);
end
if ~found
dists = abs(rows - r(k-1));
[~, min_idx] = min(dists);
row_indices = rows(min_idx);
col_indices = cols(min_idx);
end
% 抛物线插值代码（开始）
row_int = round(row_indices); % 整数行位置
col_int = round(col_indices); % 整数列位置
% 边界位置保持原像素级结果
if row_int > 1 && row_int < size(R,1) && col_int > 1 && col_int < size(R,2)
% 行方向（y轴）抛物线插值：上下相邻3个点的相关系数
y0 = R(row_int-1, col_int); % 上邻点（整数索引）
y1 = R(row_int, col_int); % 最大值点（整数索引）
y2 = R(row_int+1, col_int); % 下邻点（整数索引）
% 抛物线插值公式：亚像素偏移量 dy = -0.5*(y2-y0)/(y2-2*y1+y0)
dy = -0.5 * (y2 - y0) / (y2 - 2*y1 + y0);
% 插值后的行亚像素位置
row_indices = row_int + dy;
% 列方向（x轴）抛物线插值：
x0 = R(row_int, col_int-1); % 左邻点（整数索引）
x1 = R(row_int, col_int); % 最大值点（整数索引）
x2 = R(row_int, col_int+1); % 右邻点（整数索引）
% 抛物线插值公式：亚像素偏移量 dx = -0.5*(x2-x0)/(x2-2*x1+x0)
dx = -0.5 * (x2 - x0) / (x2 - 2*x1 + x0);
% 插值后的列亚像素位置
col_indices = col_int + dx;
end
r(k) = row_indices;
c(k) = col_indices;
end
pluse=-(r-(p+1));
plot(pluse);
elapsed_time = toc;
% 输出运行时间
fprintf('程序总运行时间：%.4f 秒\n', elapsed_time);
save('pluse_MSD1',"pluse")针对 pluse_MSD1、pluse_MAD1、pluse_NCC1 三组数据，首先采用 Savitzky-Golay（SG）滤波算法进行平滑处理，随后分别计算各滤波结果与真实参考值（data）之间的均方根误差（RMSE），以量化评估滤波效果。以下为实现该过程的 Python 代码：
python
import scipy.io as sio
import numpy as np
from scipy.signal import savgol_filter
import matplotlib.pyplot as plt
data_path = "C:/Users/admin/Desktop/图像运动分析/data.mat" # 真实值文件
msd_path = "C:/Users/admin/Desktop/图像运动分析/pluse_MSD1.mat" # pluse_MSD1文件
mad_path = "C:/Users/admin/Desktop/图像运动分析/pluse_MAD1.mat" # pluse_MAD1文件
ncc_path = "C:/Users/admin/Desktop/图像运动分析/pluse_NCC1.mat" # pluse_NCC1文件
scale = 0.077
sg_window = 11 # SG滤波窗口长度
sg_poly = 2 # SG滤波多项式阶数
true_data = sio.loadmat(data_path)["pluse_t"].flatten()
msd_data = sio.loadmat(msd_path)["pluse"].flatten() * scale
mad_data = sio.loadmat(mad_path)["pluse"].flatten() * scale
ncc_data = sio.loadmat(ncc_path)["pluse"].flatten() * scale
min_len = min(len(true_data), len(msd_data), len(mad_data), len(ncc_data))
x_axis = np.arange(min_len)
true_data = true_data[:min_len]
msd_data = msd_data[:min_len]
mad_data = mad_data[:min_len]
ncc_data = ncc_data[:min_len]
msd_filtered = savgol_filter(msd_data, sg_window, sg_poly)
mad_filtered = savgol_filter(mad_data, sg_window, sg_poly)
ncc_filtered = savgol_filter(ncc_data, sg_window, sg_poly)
def calc_rmse(pred, true):
return np.sqrt(np.mean((pred - true) ** 2))
msd_rmse = calc_rmse(msd_filtered, true_data)
mad_rmse = calc_rmse(mad_filtered, true_data)
ncc_rmse = calc_rmse(ncc_filtered, true_data)
# 输出RMSE结果
print("===== RMSE计算结果 =====")
print(f"pluse_MSD1 滤波后RMSE: {msd_rmse:.6f}")
print(f"pluse_MAD1 滤波后RMSE: {mad_rmse:.6f}")
print(f"pluse_NCC1 滤波后RMSE: {ncc_rmse:.6f}")
#可视化
plt.plot(x_axis, true_data, 'k-', label='真实值 (pluse_t)', linewidth=2)
plt.plot(x_axis, msd_data, 'r--', label='原始数据 (pluse_MSD1)', alpha=0.6)
plt.plot(x_axis, msd_filtered, 'b-', label=f'SG滤波后 (RMSE={msd_rmse:.4f})', linewidth=1.5)
plt.title("pluse_MSD1 原始数据、SG滤波结果与真实值对比")
plt.xlabel("数据点索引")
plt.ylabel("数值")
plt.legend()
plt.grid(alpha=0.3)
plt.plot(x_axis, true_data, 'k-', label='真实值 (pluse_t)', linewidth=2)
plt.plot(x_axis, mad_data, 'r--', label='原始数据 (pluse_MAD1)', alpha=0.6)
plt.plot(x_axis, mad_filtered, 'b-', label=f'SG滤波后 (RMSE={mad_rmse:.4f})', linewidth=1.5)
plt.title("pluse_MAD1 原始数据、SG滤波结果与真实值对比")
plt.xlabel("数据点索引")
plt.ylabel("数值")
plt.legend()
plt.grid(alpha=0.3)
plt.plot(x_axis, true_data, 'k-', label='真实值 (pluse_t)', linewidth=2)
plt.plot(x_axis, ncc_data, 'r--', label='原始数据 (pluse_NCC1)', alpha=0.6)
plt.plot(x_axis, ncc_filtered, 'b-', label=f'SG滤波后 (RMSE={ncc_rmse:.4f})', linewidth=1.5)
plt.title("pluse_NCC1 原始数据、SG滤波结果与真实值对比")
plt.xlabel("数据点索引")
plt.ylabel("数值")
plt.legend()
plt.grid(alpha=0.3)3 结果分析
从表 1 和图 2 可以看出，不同参数和方法对径向位移估计精度的影响具有明显规律：三种方法（MSD、MAD、NCC）在使用 SG 滤波后，RMSE 均明显低于未滤波状态，说明 SG 滤波能有效抑制噪声，提升位移估计的精度。其中，MSD 方法在所有参数组合下的 RMSE 始终保持最低，表现出最强的抗噪能力和估计稳定性。当多项式阶数固定为 p=2 时，随着窗口大小 m 从 5 增加到 11，三种方法的 RMSE 整体呈下降趋势，说明适度增大窗口能更好地平滑信号。当窗口 m=11 时，所有方法均达到各自的最低 RMSE：MSD: 0.009845MAD: 0.014732NCC: 0.015584当窗口继续增大到 m=13 时，RMSE 出现回升，表明过度平滑会丢失脉搏波的细节特征，导致估计偏差增大。图 2 中，MSD、MAD、NCC 的滤波后曲线（蓝色）与真实值曲线（黑色）高度重合，而原始数据曲线（红色）存在明显波动。特别是 MSD 的滤波结果，几乎与真实值完全重叠，直观印证了其在定量分析中的精度优势。
|----------|----------|----------|----------|
| 参数 | MSD | MAD | NCC |
| 未滤波 | 0.011280 | 0.018287 | 0.017139 |
| p=2,m=5 | 0.010451 | 0.016275 | 0.016418 |
| p=2,m=7 | 0.010008 | 0.015445 | 0.015969 |
| p=2,m=9 | 0.009898 | 0.014908 | 0.015704 |
| p=2,m=11 | 0.009845 | 0.014732 | 0.015584 |
| p=2,m=13 | 0.010319 | 0.015075 | 0.015862 |
[表1 不同参数的径向位移定量分析（RMSE）]
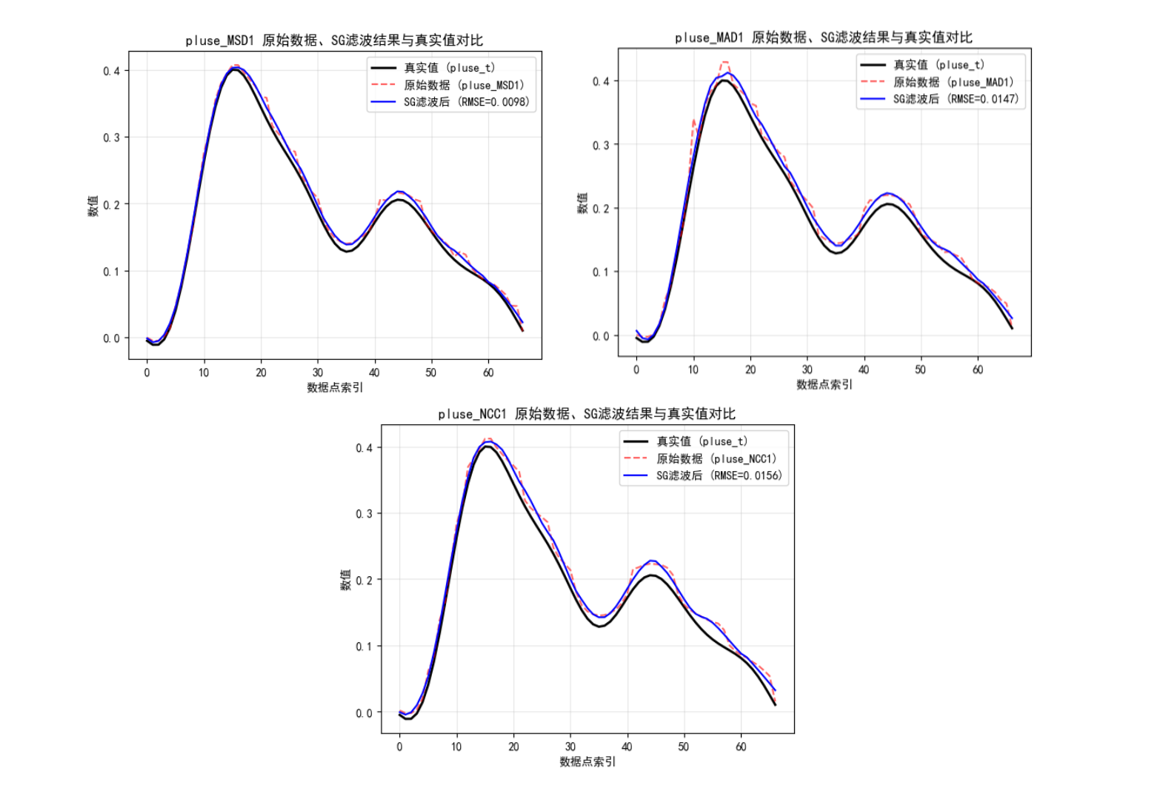图2 基于SG滤波的参数（m=11,p=2）的径向位移估计结果
4 讨论
本文围绕脉搏波径向位移估计的精度提升问题，系统评估了 SG 滤波在不同参数组合下对 MSD、MAD 和 NCC 三种方法的优化效果。结果表明，SG 滤波能显著提升位移估计精度，滤波后三种方法的均方根误差（RMSE）均明显低于未滤波状态，证实其具有良好的噪声抑制能力。在三种方法中，MSD 方法在所有参数组合下均表现出最低的 RMSE，展现出最强的抗噪性能和估计稳定性。进一步分析显示，当固定多项式阶数为 p=2 时，窗口大小 m 从 5 增至 11，三种方法的 RMSE 整体呈下降趋势，说明适度增大窗口有助于平滑信号、提升估计精度。在 m=11 时，各方法达到最优估计效果，其中 MSD 的 RMSE 最低（0.009845），MAD 和 NCC 分别达到 0.014732 和 0.015584。但当窗口进一步增大至 m=13 时，RMSE 出现回升，提示窗口过大可能导致过度平滑，损失脉搏波的细节信息，从而引入估计偏差。从图 2 的波形对比可见，滤波后曲线（蓝色）与真实值曲线（黑色）高度吻合，原始数据曲线（红色）则波动明显，进一步验证了滤波处理在提升信号质量方面的有效性。尤其是 MSD 滤波后的曲线几乎与真实值完全重叠，综上，合理配置 SG 滤波参数，尤其是选用适中窗口大小和以 MSD 为目标方法，可显著提升脉搏波径向位移的估计精度，为后续生理信号分析提供了可靠依据。
值得注意的是，结论是基于特定数据集和实验条件得出的。在实际临床场景中，脉搏波信号可能受到运动伪影、个体差异、测量设备等多种因素的影响，SG 滤波的最优参数可能需要根据具体情况进行调整。未来的工作可以从以下几个方面展开：一是探索自适应 SG 滤波策略，根据信号的局部特征动态调整窗口大小和多项式阶数；二是将深度学习方法（如 CNN、Transformer）与传统滤波技术相结合，构建端到端的位移估计模型；三是扩大数据集规模，纳入更多不同年龄、性别和健康状况的样本，以验证方法的泛化能力。
5 参考
1\]刘明波,何新叶,杨晓红,等.《中国心血管健康与疾病报告2023》要点解读\[J\].中国心血管杂志,2024,29(04):305-324. \[2\] 孙园园.基于超声图像的颈动脉运动估计\[D\].哈尔滨工业大学,2017. \[3\] [MATLAB：一种超声图像的运动分析方法（块匹配法）-CSDN博客](https://blog.csdn.net/weixin_74961953/article/details/157141385?spm=1001.2014.3001.5502 "MATLAB：一种超声图像的运动分析方法（块匹配法）-CSDN博客") \[4\] [MATLAB：一种超声图像的运动分析方法（改进的块匹配法）-CSDN博客](https://blog.csdn.net/weixin_74961953/article/details/157658227?spm=1001.2014.3001.5502 "MATLAB：一种超声图像的运动分析方法（改进的块匹配法）-CSDN博客") \[5\] [高精度保形滤波器Savitzky-Golay的数学原理、Python实现与工程应用 - 知乎](https://zhuanlan.zhihu.com/p/15150056298 "高精度保形滤波器Savitzky-Golay的数学原理、Python实现与工程应用 - 知乎") \[6\][基于 PPG 时频域特征融合与多机器学习算法的心理压力智能诊断模型研究-CSDN博客](https://blog.csdn.net/weixin_74961953/article/details/155206039?spm=1001.2014.3001.5502 " 基于 PPG 时频域特征融合与多机器学习算法的心理压力智能诊断模型研究-CSDN博客") \[7\] Gu O, He B, Xiong L, et al. Reconstructive interpolation for pulse wave estimation to improve local PWV measurement of carotid artery\[J\]. Medical \& Biological Engineering \& Computing, 2024, 62(5): 1459-1473. \[8\] Mo H, Lang X, Zhang Y, et al. Optimally filtering and matching processing for regional upstrokes to improve ultrasound transit time-based local PWV estimation\[J\]. Computer Methods and Programs in Biomedicine, 2022, 224: 106997. \[9\]基于多源信息融合的颈动脉局部脉搏波速估计\[J/OL\].生物医学工程学杂志,1-8 注：若有侵权部分，请留言将会删除。 个人观点，仅供参考