整型数据在内存中以补码形式存储,便于统一处理符号位和数值运算。正数的原码、反码、补码相同,负数则需转换。大端和小端是两种字节序存储方式,区别在于高低位的存放顺序。浮点数存储采用IEEE 754标准,分为符号位、指数位和尾数位,其读取规则与整型不同。通过代码示例展示了整型和浮点型数据在内存中的存储差异及读取方式。
整形数据在内存中的存储
我们整形在内存中以2进制进行储存
2进制形式 有原码 反码 补码
我们在计算机中看到的是原码 而进行计算的是补码
正数
正数的原码 反码 补码相同
最高位是符号位 0表示正 1表示负
负数
负数 的原码 补码 反码不同
负数的原码变 反码 符号位不变 其他取反 0变1 1变0
原码变补码 反码+1
补码变反码 一样
对于整形来说:数据存放内存中其实存放的是补码。
为什么呢?
在计算机系统中,数值⼀律⽤补码来表⽰和存储。
原因在于,使⽤补码,可以将符号位和数值域统⼀处理;
同时,加法和减法也可以统⼀处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是
相同的,不需要额外的硬件电路。
大端和小端
大端和小端是关于字节序存储的方式 无论大端和小端在内存中虽然不一样但取出来的值一样

我们看到在内存中10以倒序放在内存中
我们把这种低位放在低地址 高位放在高地址的顺序叫做小端
相反
以高位放在低地址 低位放在高地址处的顺序叫大端
那么什么叫低位 什么叫高位 低地址和高地址
我们把在内存中的存储想成一个数组 我们数组的地址是不是由低地址向高地址
低位是最右边的数字 越往左越高 个十百千万
大小端的判断代码
int duan(int *a)
{
return *(char*)&a;
}
int main()
{
int a = 1;//00000001
int b=duan(a);
if (b == 1)
{
printf("小端");
}
if (b == 0)
{
printf("大端");
}
return 0;
}
整形计算 #include <stdio.h>
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf("a=%d,b=%d,c=%d",a,b,c);
return 0;
}



浮点数在内存中是怎样存储的?
#include <stdio.h>
int main()
{
int n = 9;
float *pFloat = (float *)&n;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
*pFloat = 9.0;
printf("num的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
return 0;
}
浮点数和整数在内存中的规则不同
二进制浮点数的公式

对于float和double 有不同的位置限制
32位的float 第一个表示s 是符号位 下一个8位是E储存 指数 然后23位是M
64位的double 第一个表示 s 是符号位 下一个11位表示E储存 指数 然后是52位是M

对于M
一般省略 1.01 省略1 只存01 这样能存24位
对于E
由于二进制的范围是0到255 E有可能是负数 所以计算时 32位的时候加上127
64位加上1023
浮点数的取出
E的特殊情况
E不为全1或不为全0
E加上127或1023 M加上1.
E为全0
E-127(1023)M为0.
E为全1
如果这是M为全0 则无穷大
int n = 9;
float* pFloat = (float*)&n;
printf("n的值为:%d\n", n);
printf("*pFloat的值为:%f\n", *pFloat);
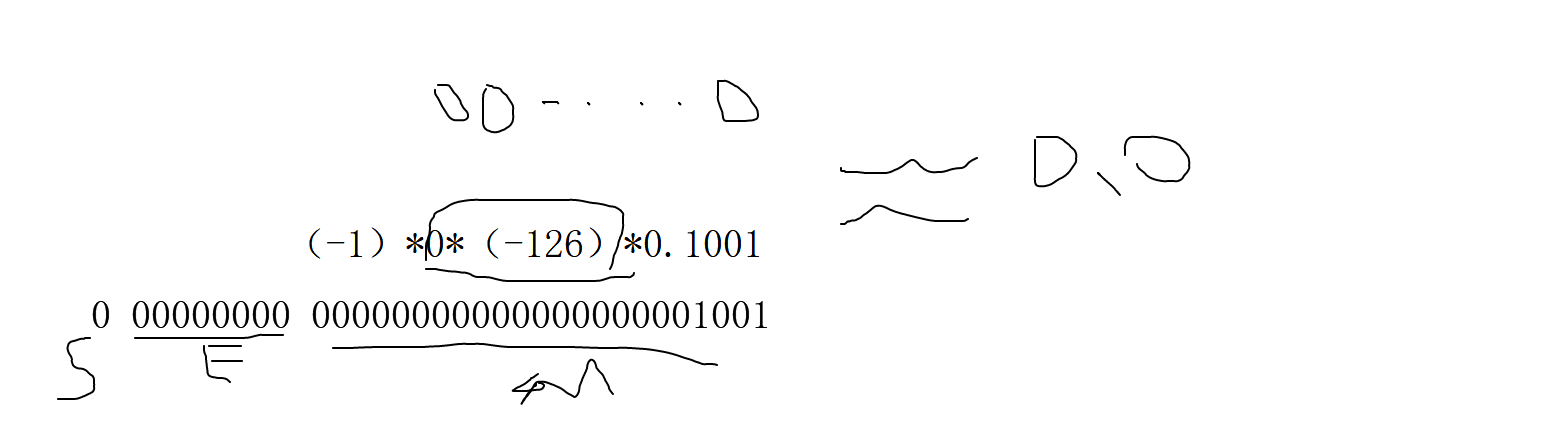
printf("%f",*pFloat)
以%f打印 正数的原码 反码和补码相同
10进制打印